Смешанное произведение

Если вектор умножить векторно на вектор , а потом получившийся вектор скалярно умножить на вектор , то полученное число называется смешанным произведением трех векторов.

Обозначается: .

Если известны координаты векторов , то

.

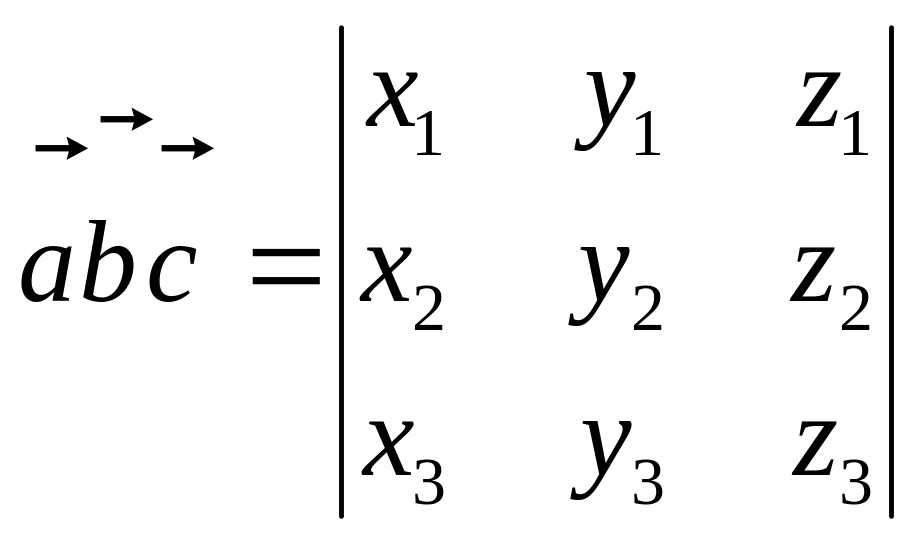Можно доказать, что модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах , как на сторонах, т.е.

- объем параллелепипеда.

- объем пирамиды.

Пример (см.задание 1.5)

Найти объем пирамиды с вершинами А₁(0,-1,2), А₂(-1,0,6), А₃(-2,1,0), А₄(0,1,4).

Решение.

.

.

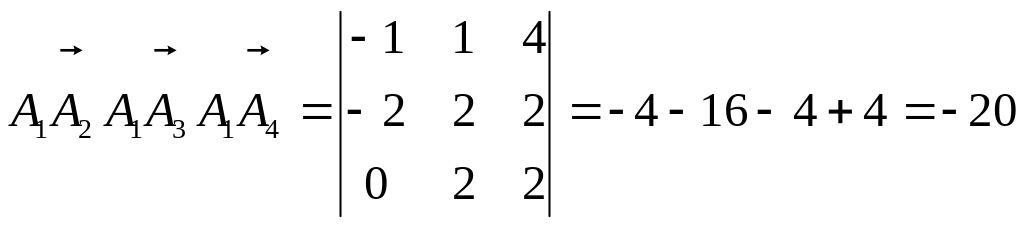Тогда объем пирамиды:

.

Ответ: .

Аналитическая геометрия Прямая на плоскости

- каноническое уравнение прямой, проходящей через заданную точку A₁(x₁, y₁), параллельно вектору .

- направляющий вектор.

- уравнение прямой, проходящей через 2 заданные точки A(x₁, y₁), A(x₂, y₂).

y

-y₁=k(x-x₁) уравнение пучка прямых с центром A(x₁, y₁) и угловым коэффициентом k.

y=kx+b уравнение прямой с угловым коэффициентом.

A

(x-x₁)+B(y-y₁)=0 уравнение прямой, проходящей через точку перпендикулярно вектору .

- нормаль прямой.

После упрощения последнего уравнения получаем:

Ax+By+C=0 - общее уравнение прямой, где C=-(Ax₁+By₁).

Угловой коэффициент прямой находим по формуле .

Угол между двумя прямыми равен углу между их нормалями или направляющими векторами (см. скалярное произведение).

Если - угловые коэффициенты двух прямых, то

при - прямые параллельны,

при - прямые перпендикулярны.

Пример

Составить уравнение прямой, проходящей через точку М(3, 4):

а) параллельно прямой 2x-5y+1=0,

b) перпендикулярно прямой 2x-5y+1=0.

Решение.

а) 2x-5y+1=0; .

.

Если прямые параллельны, то .

Используем уравнение y-y₁=k(x-x₁), где , М(3, 4).

y-4= (x-3);

5(y-4)=2(y-3);

2x+5y+14=0.

b) Если прямые перпендикулярны, то .

;

;

.

Прямая в пространстве

к

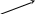аноническое уравнение прямой в пространстве, проходящей через точку A₁(x₁, y₁, z₁), параллельно вектору .

-- направляющий вектор.

Замечание. Если обращается в ноль одна из координат направляющего вектора, например m , то уравнение прямой принимает вид:

-

это прямая, лежащая в плоскости x=x₁.

Если равны нулю две координаты направляющего вектора, например m=n=0, то уравнение прямой примет вид:

- эта прямая есть пересечение двух плоскостей x=x₁ и y=y₁, то есть параллельна оси OZ.

- уравнение прямой, проходящей через две точки .

Пример (см. задание 1.6)

Составим уравнение прямых А₁, А₂ и А₁А₃.

А₁(2, 0, 3), А₂(-1, 0, 8), А₃(0, 2, 4).

Воспользуемся уравнением прямой, проходящей через две точки:

;

;

-- уравнение прямой A₁A₂.

Эта прямая лежит в плоскости (т.е. в плоскости OXZ) и ее уравнение можно записать так:

.

Плоскость в пространстве

- уравнение плоскости, проходящей через точку , перпендикулярно вектору - нормали к плоскости.

-- уравнение плоскости, проходящей через три заданные точки .

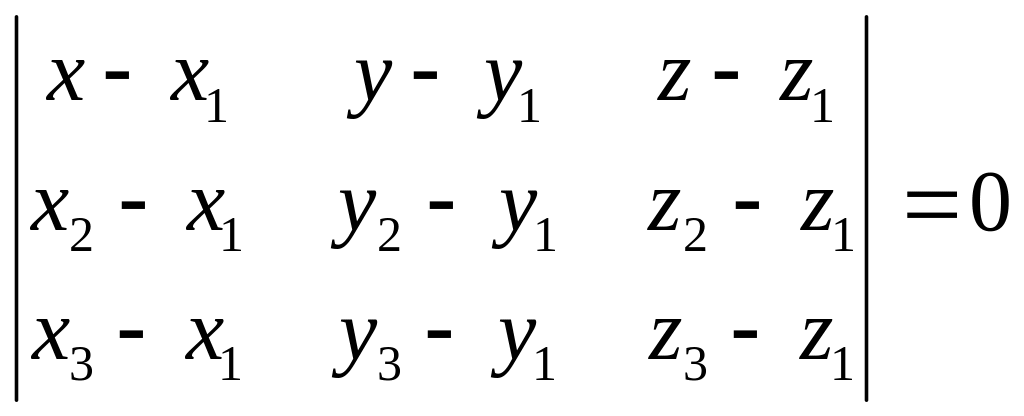
Если две плоскости заданы общими уравнениями:

то по уравнениям двух плоскостей можно определить их нормали .

На основании теоремы об углах, образованных взаимно перпендикулярными сторонами, один из углов между плоскостями можно определить как угол между нормалями по формуле:

.

Пример (см.задание 1.7)

Составить уравнение плоскости А₁А₂А₃, если А₁(2, 0, ,3), А₂(-1, 0, 8), А₃(0,2,4).

Воспользуемся уравнением плоскости, проходящей через три точки:

,

,

.

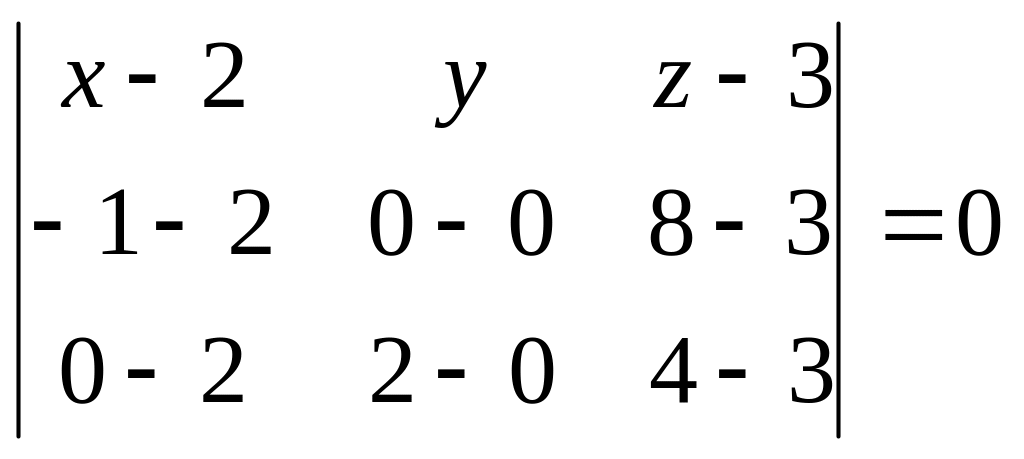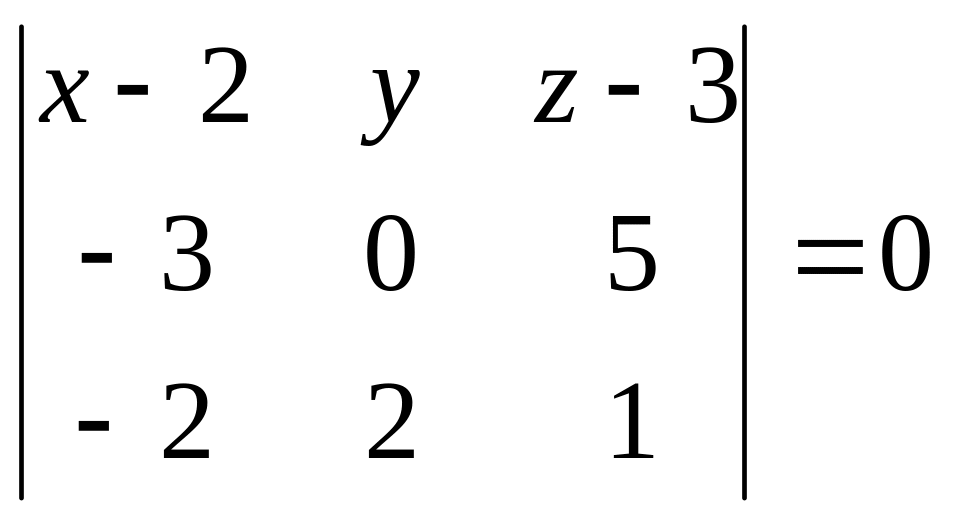Раскроем определитель:

(x-2)∙0+y∙5∙(-2)+(z-3)∙(-3)∙2-(z-3)∙0-(x-2)∙2∙5-y∙(-3)∙1=0;

-10(x-2)-7y-6(z-3)=0;

-10x-7y-6z+38=0 –

уравнение плоскости А₁А₂А₃.