5. Современные подходы к описанию механики процесса резания

Основными методами теории пластичности, используемые при решении задач процессов резания, являются: метод нижней оценки, метод верхней оценки, метод линий скольжения, а также решение дифференциальных уравнений равновесия совместно с условием пластичности. Решение задач выполнено с учетом контактных явлений при обработке материалов резанием, износа режущего инструмента, скругления режущей кромки и упругой деформации инструмента и обрабатываемого материала.

Элементы теории разрушения использованы для оценки нарушения сплошности срезаемого слоя при переходе его в стружку, а также для оценки степени повреждаемости поверхности, обработанной резанием.

Решению задач предшествует краткое рассмотрение элементов теории напряжений, теории деформаций и уравнений связи между напряжениями и деформациями, а также условия перехода деформируемого материала в пластическое состояние.

М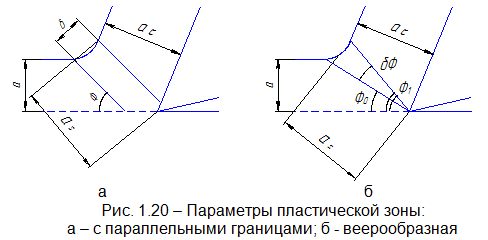 атематические зависимости являются универсальными и могут быть использованы при инженерных расчетах по оценке энергосиловых параметров, качественных показателей состояния поверхностного слоя, типа образующейся стружки, профиля изношенного инструмента, применительно к различным операциям механической обработки: точению, сверлению, фрезерованию, строганию, протягиванию и т.п.

При схематизации зоны стружкообразования одной плоскостью сдвига или областью с параллельными границами ее положение характеризуется углом наклона условной плоскости сдвига  (рис. 1.20, а). В схемах стружкообразования с веерообразной переходной пластической зоной ее положение определяют углом наклона конечной границы. ₁. (рис. 1.20, б).

Размеры зоны пластической деформации в моделях стружкообразования с единственной плоскостью сдвига характеризуется ее длиной, в моделях с параллельными границами – длиной и расстоянием между начальной и конечной границами этой зоны  и в моделях с веерообразной пластической зоной – длиной и углом между границами  (рис. 1.20, б).

При использовании схем стружкообразования с криволинейными границами переходной пластически деформированной зоны дополнительной характеристикой служит их кривизна.

Используя различные схемы стружкообразования и гипотезы, получили соотношения для угла сдвига.

Анализируя схему сил для модели стружкообразования с единственной плоскостью сдвига и используя гипотезу о минимуме усилий резания К.А. Зворыкин получил следующее выражение для угла сдвига

, (1.7)

где  - угол внутреннего трения;  - угол трения стружки о переднюю поверхность резца;  - передний угол.

А.А. Брикс вывел соотношение для модели с веерообразной зоной пластической деформации, определяющее положение ее конечной границы , (1.8)

где ₁ – угол наклона касательной, проведенной к наружной границе зоны стружкообразования в точке ее пересечения с наружной поверхностью стружки.

Х. Эрнст и М.Е. Мерчант, применяя принцип минимума работы резания к модели с одной плоскостью сдвига, получили формулу: , (1.9)

Оценка величины зоны пластической деформации

В.К. Старков [176] для расчета длины опережающего упрочнения перед вершиной резца предлагает формулу: , (1.26) где g – показатель распределения напряжения перед резцом, z – действующее напряжение перед резцом, 0,2 – условный предел текучести обрабатываемого материала.

Аналитическое выражение для определения ширины зоны пластической деформации получено В.И. Садчиковым: (1.27)

где:  – параметр, определяемый соотношением ,

0, 0 – касательное и нормальное напряжения, действующие по условной плоскости сдвига.

Определения скорости деформации

Наиболее распространенной формулой, используемой для расчета скорости деформации является:

,

где v – скорость резания, δ – толщина зоны пластической деформации.

Используя те или иные допущение о размерах зоны пластической деформации можно получить расчетные значения скорости деформации.

Ориентировочно толщину зоны пластической деформации рассчитывают по зависимости: ,

где к – коэффициент, определяемый экспериментально; а – толщина среза; φ – угол сдвига.

По разным данным величина коэффициента к изменяется в пределах 2,6…10.

П.Б. Оксли использовал эмпирическую зависимость: ,

где с – постоянная материала; vs – скорость сдвига; as – длина плоскости сдвига.

Для углеродистых сталей постоянная с = 5,9. Автор указывает, что эта зависимость справедлива в диапазоне скоростей деформации от 1 до 10 с-1. Для более высоких скоростей деформации она дает большие отклонения от экспериментальных данных.

В.С. Кушнер предлагает использовать формулу для определения скорости деформации в зоне резания в виде: ,где υs – разрыв касательной скорости относительно условной плоскости сдвига; n – параметр, характеризуемый степень неоднородности сдвига; Y – текущее значение координаты по толщине переходной пластически деформированной зоны стружкообразования.

При обработке стали твердосплавным резцом, величина n изменяется в пределах 4-8.

Полагая величину δ равной половине толщины срезаемого слоя автор получил для типичных условий резания множитель порядка 104 с-1.

Недостатком всех вышеприведенных формул является то, что они не учитывают тип образующейся стружки.

Зависимость для расчета скорости деформации материала при стружкообразовании с учетом вида, образующейся стружки имеет вид: , где υ – скорость резания, А – коэф сплошности стружки.

.где К1 – вязкость разрушения при плоском деформированном состоянии, МПа;

а – толщина среза, м; υ – скорость резания, м/с; – предел прочности обрабатываемого материала на срез, МПа; ρ – плотность обрабатываемого материала, МПа с2/м2.

Аналитические методы расчета составляющих силы резания не учитывают вид образуемой стружки и разработаны из предположения, что режущий инструмент является абсолютно жестким.

В большинстве случаев для моделей стружкообразования с единственной плоскостью сдвига или с прямолинейными границами зоны пластической деформации используется условие равновесия стружки (рис. 1.36).

Если допустить, как это было принято в работах, что касательные напряжения по плоскости сдвига равны пределу прочности обрабатываемого материала на сдвиг, то из схемы сил следует:

, (1.68)

где _S - предел прочности обрабатываемого материала на сдвиг;

 - угол наклона равнодействующей силы резания к плоскости сдвига.

Таким образом, знание угла сдвига  и угла наклона равнодействующей силы резания к плоскости сдвига , позволяет определить величину этой равнодействующей, используя довольно простое соотношение (1.68). Этим объясняется тот факт, что, как правило, расчетные методы определения силы резания прямо или косвенно сводятся к установлению значения угла  или к выражению его через известные параметры процесса резания (угол сдвига, угол трения и т.д.).

Существуют также формулы не требующие прямого определения величины угла наклона равнодействующей сил резания к плоскости сдвига. Такие формулы для определения главной составляющей силы резания получены [99]:

Т.Н. Лоладзе Р_z = 2,6_sts, (1.69)

Н.И. Резниковым , (1.72)

П.А. Горезко Р_z = _вав(+1), (1.74)

Л.М. Седоковым Р_z = _sав(Г+1), (1.75)

Г.И. Грановским ,(1.73)

В приведенных формулах использованы следующие обозначения:

₀ – условный предел текучести при сжатии,_в – предел прочности обрабатываемого материала при растяжении,т – показатель политропы сжатия,С_v – объемная теплоемкость,, ₁ – коэффициенты трения по передней и задней поверхностям режущего инструмента,_пл – температура плавления обрабатываемого материала._з – температура припуска, – температуропроводность,D – диаметр обрабатываемой заготовки.