3. Обобшенные зависимости между статическими и кинематическими параметрами рабочей части инструмента.

Статическая система координат – прямоугольная система координат с началом в рассматриваемой точке режущей кромки, ориентированная относительно направления скорости главного движения резания.

Кинематическая система координат – прямоугольная система координат с началом в рассматриваемой точке режущей кромки, ориентированная относительно направления скорости результирующего движения резания.

Г еометрию любого инструмента следует рассматривать в двух аспектах: в статике и в кинематике. В первом случае инструмент рассматривается как геометрическое тело, т.е. его углы интересуют нас как параметры конструкции, которые нужно выполнить и проконтролировать согласно чертежу. Во втором случае углы инструмента рассматриваются в процессе резания, когда их фактические значения могут измениться в зависимости от режимов резания и точности установки инструмента относительно обрабатываемой заготовки.

Для рассмотрения геометрии конкретного вида инструмента в статике выбирается наиболее удобная система координат, в которой однозначно определяются все его геометрические параметры. Такой системой могут являться три взаимно перпендикулярные плоскости (рис. 2): опорная X0Y, продольная Y0Z и поперечная X0Z.

На практике для определения углов резца чаще используют следующие координатные плоскости:

Плоскость резания – пл-ть, касательная к пов-ти резания и проходящая через главную режущую кромку резца.

Основная плоскость – пл-ть, параллельная продольному (параллельно оси заготовки) и поперечному (перпендикулярно оси заготовки) перемещениям резца.

Главная секущая плоскость N-N – пл-ть, перпендикулярная к пов-ти гл режй кромки на основную плоскость.

Вспом секущая пл-ть N₁-N₁ – пл-ть, перпендикулярная к проекции вспомог реж кромки на основную плоскость.

Главные углы резца измеряются в главной секущей плоскости (рис. 3), к ним относятся:

Главный задний угол α – угол между главной задней поверхностью и плоскостью резания.

Угол заострения β – угол между передней и главной задней поверхностями резца.

Передний угол γ – угол между передней пов-тью резца и плоскостью, перпендикулярной к плоскости резания.

Угол резания δ – угол между передней поверхностью резца и плоскостью резания.

Как видно из рис. 3, между четырьмя главными углами существуют следующие зависимости:

α + β + γ = 90° ; δ + γ = 90° ; δ = α + β = 90° – γ .

К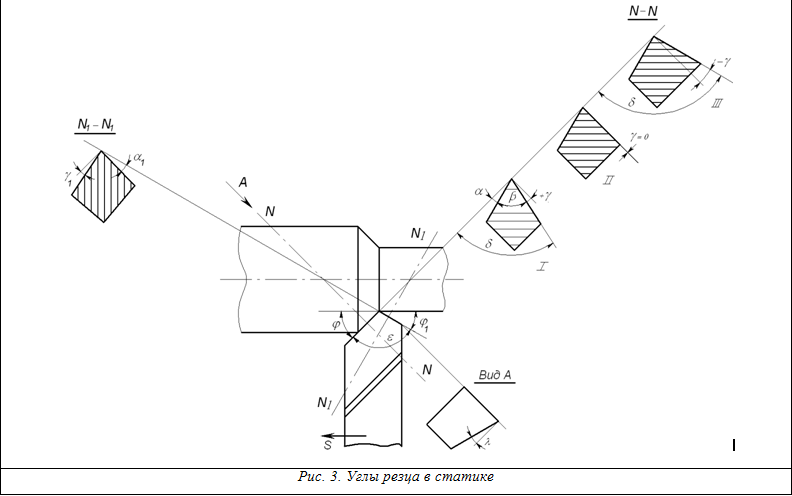 огда угол резания δ < 90° (рис. 3, I) считается, что угол γ > 0 ; когда δ > 90°, угол γ < 90° (рис. 3, III).

Вспомогательные углы измеряются во вспомогательной секущей плоскости, к ним относятся:

Вспомогательный задний угол α₁ – угол между вспомогательной задней пов--тью и пл-тью, проходящей через вспомогательную реж кромку перпендикулярно к основной пл-ти. Вспомогательный передний угол γ₁ также измеряют во вспомогательной секущей плоскости N₁-N₁.

Также, резец имеет углы в плане и угол наклона главной режущей кромки. Углы в плане измеряют в основной плоскости:

Гл угол в плане φ – угол между проекцией главной режущей кромки на основную плоскость и направлением подачи.

Вспом. угол в плане φ₁ – угол м/у проекцией вспомогательной реж кромки на основ пл-ть и направлением подачи.

Угол при вершине в плане ε – угол м/у проекциями гл и вспом режущих кромок на основную плоскость.

Как видно из рис. 3 между углами в плане существует зависимость: φ + φ₁ + ε = 180°.

У гол наклона главной режущей кромки λ – угол, заключенный м/у гл реж. кромкой и пл-тью, проведенной через вершину резца параллельно основной плоскости. Этот угол измеряется в плоскости, проходящей через главную режущую кромку, перпендикулярно к основной плоскости. Угол наклона главной режущей кромки считается положительным, когда вершина резца является низшей точкой режущей кромки (рис. 4, в); равным нулю – при главной режущей кромке, параллельной основной плоскости (рис. 4, б) и отрицательным – когда вершина резца является наивысшей точки режущей кромки (рис. 4, а).

У глы резца при установке на станке. Выше рассматривались углы резца как геометрического тела, находящегося в состоянии покоя, при расположении точек его режущей кромки на уровне оси центров станка, а оси резца – перпендикулярно оси центров (рис. 6, а). При подъеме и опускании точек режущей кромки относительно линии центров значения углов γ, α и δ будут изменяться.

В случае установки режущей кромки резца выше линии центров станка изменяется положение плоскости резания (рис. 6, б), передний угол при этом увеличивается, а задний угол уменьшается. При установке ниже линии центров (рис. 6, в) указанные углы изменяются наоборот: передний угол уменьшается, а задний угол увеличивается.

Р ассмотрим случай, когда вершина резца расположена ниже оси центров на величину h (рис.6, в), а углы l и j равны нулю. При расположении вершины резца по центру заготовки передний и главный задний углы соответственно равны и . Если вершину резца опустить ниже оси заготовки на величину h, то статическая система координат повернется на угол μ и углы будут соответственно равны и . Из рисунка видно, что угол уменьшился, а угол увеличился на величину угла μ. Соответственно углы и будут равны:

Если угол будет отличен от нуля (j¹0), угол можно найти как

Тогда .

Если вершина резца будет расположена выше оси центров, знаки в формулах для определения углов и меняются на противоположные. На практике чаще всего устанавливают резец по оси центров.

Углы резца в кинематике. Рассмотренные углы резца представляют собой углы в статическом состоянии, т.е. когда резец не работает. В процессе резания статические углы изменяются. Изменение величин переднего и заднего углов вызывается сложным относительным движением инструмента и заготовки, в результате чего изменяется положение поверхности резания.

В случае продольного точения заготовка имеет вращательное движение, а резец получает поступательное движение вдоль оси заготовки. Следовательно, поверхность резания представляет собой винтовую поверхность (рис. 7).

Д ействительный задний угол будет иметь величину: α_k = α – μ и tg μ = ,где μ – угол подъема винтовой линии, α – угол заточки, S – подача в мм/об, D – диаметр заготовки в мм.

С увеличением подачи и уменьшением диаметра заготовки угол μ увеличивается, а, следовательно, уменьшается действительный задний угол α_к. Действительный передний угол γ_к соответственно увеличивается.

С учетом этого

Е сли угол j будет отличен от 90^о (j¹90°), выражение для определения углов и будут равны:

При поперечном точении в результате сочетания вращательного движения заготовки и поперечного перемещения резца траекторией движения точек режущей кромки является архимедова спираль, касательная к которой будет действительной плоскостью резания.

Чем ближе режущая кромка к центру заготовки (рис. 8), тем круче спираль и тем больше будет отклоняться касательная А-А к спирали от плоскости резания В-В, касательной к окружности в статическом состоянии. Вследствие этого действительный задний угол будет непрерывно уменьшаться, а передний – увеличиваться.

По аналогии с предыдущим случаем имеем (рис.8):

Из полученных выражений следует, что главный задний угол надо выбирать таким, чтобы на любом диаметре угол αк был больше нуля.

Таким образом, углы α и γ (полученные после заточки) претерпевают изменения во время установки резца и при движении инструмента и заготовки. Эти изменения необходимо заранее учитывать при выборе значений углов инструмента для конкретных условий обработки.