11. Научные подходы к оптимизации режимов резания при лезвийной обработке.

При проектировании конкретной технологической операции механообработки необходимо назначить конструкцию и геометрические параметры режущего инструмента, марку инструментального материала, тип и модель станка, параметры режима обработки, оснастку, состав СОЖ и условия ее использования и т.д. Научно обоснованный подход к выбору указанных факторов операции может быть обеспечен процедурой оптимизации, при которой их назначение осуществляется в соответствии с принятым критерием оптимальности и с выполнением заданных ограничений. При этом критерий оптимальности определяет цель оптимизации, а технологические ограничения – реализацию необходимых требований к процессу обработки.

1. Выбираем характеристику режущего инструмента.

2. Выбираем глубину резания исходя из чертежа, припусков на обработку.

Максимально возможная глубина резания равна припуску, ос­тавленному на обработку. Если нет ограничений по точности обра­ботки, то весь припуск срезают за один проход. В противном случае припуск разбивают на черновые и чистовые проходы. При этом глу­бина резания черновых проходов должна быть возможно большей, а на чистовой проход следует оставлять такой минимальный припуск, который обеспечит изготовление детали с заданным допуском. 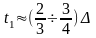, , Δ – припуск на обработку.

3. Выбираем технологически-допустимую величину подачи.

Максимально допустимая подача, как правило, ограничива­ется:

Ограничения накладываемые на величину подачи при черновой и чистовой обработке:

Прочность твердосплавной, композитной или минералокерам. реж. Пластины. Условие для проверки ломающей подачи Sл.

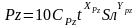
Допускаемая жесткость обрабатываемой детали:

1. При креплении в патроне:

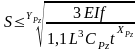
2.В центрах: 3. Патрон и центр: ,

где Е - модуль упруго­сти материала обрабатываемой детали, н/мм2;

f - допускаемая стрела прогиба детали, мм;(f черн=0,2 мм, f чист=(0,2…0,25)Δ, где Δ – допуск на размер обр. поверхности), L -вылет детали, I – момент инерции обрабатываемой детали (I=0,05D4мм4)

3. Жесткость резца: , где В и H- высота и ширина державки резца, мм; l - вылет резца, мм. Е1- модуль упругости материала державки резца, н/мм2; fp - допускаемая стрела изгиба резца, мм. (fрчерн ≤0,1 мм)

4. Прочность державки режущего инструмента: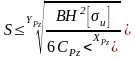

5. Прочность механизма подачи:

От мощности станка NCT: SN cm = [1 950 000 Ncm/(Dntxp)]^1/ур мм/об.

от крутящего момента станка S_Mcm= [2 000 Мст/(СpDtхр)] ^1/ур мм/об.

8. от шероховатости (при чистовой обработке):

где [σu] - допускаемое напряже­ние при изгибе для материала детали, н/мм2;

Из всех рассчитанных значений подачи выбирают минималь­ное, которое корректируют по паспорту станка, принимая действи­тельную подачу sд.

4. Устанавливают стойкость режущего инструмента.

5. Рассчитывают допускаемую скорость резания.

6.Рассчитывают число оборотов, соответствующих допускаемой скорости резания.

V-скорость резания, м/мин, D-мм

7. Корректируем, если ступенчатая коробка принимаем ближайшее меньшее значение. Ближайшее большее можно принимать только тогда, когда это увеличение составит не более 5%.

8. Рассчитываем фактическую скорость резания.

где n- скорректированное число станков

9. Проверить ограничения по мощности - рассчитываем тангенсальную составляющую силы резания.

где KPZ – коэф, оказывающий влияние на силу резания

10. Проверяем возможность выполнения операций ,

11. Считаем трудоемкость по величине машинного (станочного) времени

где L1 – величина врезания в материал; , L2 – величина перемещения, перебега, L2 =2…3 мм., L3 – длина обрабатываемой поверхности.

В настоящее время для расчетов оптимальных режимов резания применяются критерии: площадь обработанной поверхности за период стойкости инструмента, технологическая себестоимость операции, приведенные затраты на обработку, прибыль предприятия, производительность труда и др.

Для большинства практических случаев в зависимости от технологических ограничений, накладываемых на оптимальный режим резания, выбор критериев оптимальности должен производиться дифференцированно с учетом особенностей производства: его характера, типа и состояния применяемого оборудования, оснастки, типоразмера инструмента и т.д.

К достоинствам экономических критериев оптимальности можно отнести достаточно полный учет экономических аспектов оптимизации процесса резания, экстремальный характер их изменения от факторов обработки. К недостаткам экономических критериев можно отнести трудности формализации некоторых их составляющих и особенно эксплуатационных показателей. Точность оценки экономических критериев зависит от точности расчета стойкости инструмента, что требует разработки достоверных и соответственно более сложных стойкостных моделей. Оптимальность режима резания зависит от факторов конкретного производства, которые должны приниматься во внимание. И, наконец, экономические критерии оптимальности прямым образом не учитывают качество обработки: точность, шероховатость обработанной поверхности и свойства поверхностного слоя детали, что сильно сужает диапазон их эффективного использования.

Качество оптимизации как процедуры выбора оптимальных технологических условий резания требует высокого качества всех составляющих ее частей: адекватности физической и математической моделей реальному процессу, а также использования современных математических методов оптимизации и электронно-вычислительной техники. Решающая роль применительно к процессам механообработки принадлежит физической и математической моделям процесса. Повышение качества используемых моделей является одной из актуальных проблем оптимизации процесса резания.

В основе большинства известных методик оптимизации лежат эмпирические зависимости стойкости инструмента, силы и мощности резания, шероховатости обработанной поверхности и т.д . от оптимизируемых параметров обработки.

Главным недостатком модели на основе эмпирических зависимостей является то, что они не учитывают взаимосвязанности влияния различных исследуемых факторов процесса резания. Факторы, влияющие на процесс резания, рассматриваются обособленно один от другого, хотя их влияние проявляется не только каждого в отдельности, но прежде всего, совместно, в определенных сочетаниях и комбинациях.