14.Правило трех сигм

Характерное свойство нормального распределения состоит в том, что в интервале [M[Х]  1] находится около 68 % из всех его результатов измерений. В интервале [M[Х]  2] - 95 %. В интервале [M[Х]  3] - 99,73 % (рис. 1.12). Следовательно, почти все результаты измерений лежат в интервале 6 (по три  в каждую сторону от M[Х]). За пределами этого интервала могут находится 0,27 % данных от их общего числа (приблизительно три из тысячи результатов измерений). Отсюда следует, что если какое-либо значение величины выходит за пределы 3, то с большой вероятностью его можно считать ошибочным.На основании этого сформулировано правило трех сигм: если при многократных измерениях (n  25…30) одной и той же величины постоянного размера сомнительный результат Х_сомн отдельного измерения (максимальный или минимальный) отличается от среднего значения более чем на 3, то с вероятностью 99,7 % он ошибочен, т.е.

если  3, (1.12)

то Х_сомн является промахом; его отбрасывают и не учитывают при дальнейшей обработке результатов измерений.

Закон нормального распределения работает при числе результатов измерений n = . В реальности получают конечное число измерений, которые подчиняются закону распределения Стьюдента. При n25 распределение Стьюдента стремится к нормальному.

16.Точечная и интервальная оценки значения измеряемой физической величины

При измерении, как уже говорилось ранее, невозможно опреде-лить истинное значение измеряемой величины. Можно лишь с большей или меньшей уверенностью оценить это значение, рассматривая его условно как параметр нормального распредел-ения. Оценка истинного значения осуществляется по числу результатов n повторных измерений величины. Чем больше n, тем точнее можно оценить истинное значение. Выделяют понятия точечной и интервальной оценок.

Точечная оценка (т.е. оценка в виде числа) истинного значения величины включает в себя оценки M[Х] и . Оценкой M[Х] является среднее арифметическое значение , его вычисляют по формуле

где Х_i – результат i-го единичного измерения.Оценкой  является среднее квадратическое отклонение s, его вычисляют по формуле

Оценки, приведенные в формулах (1.13) и (1.14), являются случайными величинами. Если провести повторное измерение и по его результатам вычислить и s, то их значения будут отличаться от прежних. Повторяя измерения и вычисляя по их результатам и s, можно получить ряд значений и s, которые также являются случайными величинами и подчиняются нормальному закону распределения. Для оценки рассеяния этих распределений используют понятие среднего квадратического отклонения среднего арифметического , являющееся оценкой среднего квадратического отклонения результата измерения. Его определяют по формуле

Точечные оценки используют в основном в научных исследованиях и разработках, когда проводят большое число измерений. Чем меньше число полученных результатов измерений, тем легче допустить ошибку при оценке параметров распределения. В таком случае важно определить не только M[X] и , но и получить уверенность, что истинное значение находится в некотором доверительном интервале. Для этого проводят интервальную оценку.

Интервальная оценка истинного значения – это доверительный интервал, в котором с заданной доверительной вероятностью Р находится истинное значение измеряемой величины.

Чаще выбирают Р = 0,9, 0,95 и 0,99.

Границы доверительного интервала определяют по формуле

-  Х_ист  + ,

где  – это доверительная погрешность (доверительная граница случайной погрешности результата измерений).

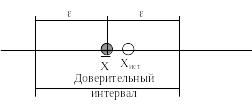
Достоверность измерений (один из показателей качества результатов) зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение лежит в указанных доверительных границах.  определяет наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной доверительной вероятностью находится истинное значение Х_ист результата измерений. Причем Х_ист может быть в любом месте доверительного интервала (не обязательно в его середине), а с вероятностью 1-Р даже вне его.При большом числе результатов измерений (n25…30) доверительную границу случайной погрешности  вычисляют по формуле

где z_р – квантиль нормального распределения (квантильный множитель),  - среднее квадратическое отклонение.

Значение квантильного множителя z_р определяют по таблице функции Лапласа при заданной доверительной вероятности Р

Чем меньше n, тем менее надежным является определение доверительного интервала приведенным выше способом.

При небольшом числе результатов измерений (n25…30) используют распределение Стьюдента, и доверительную границу случайной погрешности  следует рассчитывать по формуле

где t_p - коэффициент Стьюдента, s – оценка среднего квадратического отклоненияЗначение коэффициента Стьюдента t_p определяют при заданной доверительной вероятности Р и числе результатов измерений n .

16.Средства измерений и их классификация.Средство изме-рений -техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической вели-чины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени. Различают следующие виды средств измерений: меры, измерительные устройства, которые подразделяются на измерительные приборы и измерительные преобразователи; измерительные установки и измерительные системы. Мера - это средство измерений, предназначенное для воспроизведения физической величины заданного размера. Измерительный прибор - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительный преобразователь - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному восприятию наблюдателем По назначению измерительные приборы разделяют на универсальные, специальные и для контроля. По конструктив-ному устройству измерительные приборы делят на механические, оптические, электрические и пневматические и др.По степени автоматизации различают измерительные приборы ручного действия, механизированные, полуавтомати-ческие и автоматические. Универсальные измерительные приборы применяют в контрольно-измерительных лабораториях всех типов производств, а также в цехах единичных и мелко-серийных производств. Универсальные измерительные приборы подразделяются: на механические: - простейшие инструменты - проверочные измерительные линейки, щупы, образцы шероховатости поверхности; - Штангенинструменты – штанге-нциркуль, штангенглубиномер, штан-генрейсмас, штангенз-убомер; - микрометрические инструменты - Микрометр, микрометрический нутромер, микрометрический глубиномер; - приборы с зубчатой передачей - индикаторы часового типа; Рычажно-механические - миниметры, рычажные скобы; опти-ческие: - вертикальные и горизонтальные оптиметры, малый и большой инструментальные микроскопы, универсальный мик-роскоп, концевая машина, проекторы, интерференционные приборы; пневматические: длинномеры (ротаметры); электрическ-ие: электроконтактные измерительные головки, индуктивные приборы, профилографы, профилометры, кругломеры. Специал-ьные измерительные приборы предназна-чены для измерения одного или нескольких параметров деталей определенного типа; например приборы для измерения (контроля) параметров коленча-того вала, распределительного вала, параметров зубчатых колес, диаметров глубоких отверстий.