Теоретические основы разработки модели с одной плоскостью сдвига.

Разработка модели с одной плоскостью сдвига основана на использовании условия равновесия материала стружки, то есть результирующая сила, приложенная к стружке в плоскости сдвига равна по величине и противоположна, направлена силе, приложенной в месте контакта стружки с передней поверхностью резца.

При анализе модели с одной плоскостью сдвига сделаны следующие допущения:

1. Вершины резца абсолютно острые;

2. Трение между заготовкой и инструментом отсутствует, то есть пренебрегаем силами, действующими по задней поверхности инструмента;

3. Деформация металла двухмерна (плоская);

4. Напряжение в плоскости сдвига распределены равномерно.

Согласно сделанным допущениям схема сил, действующая в зоне резания, будет следующая:

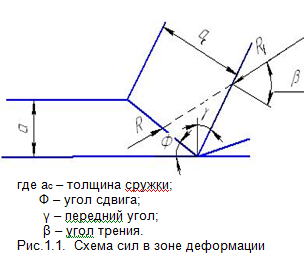
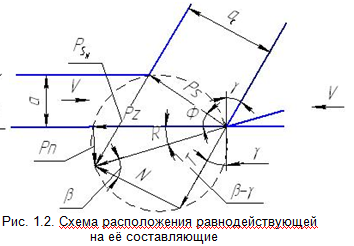
(1.1)где - предел прочности обрабатываемого материала на сдвиг; a - толщина среза;b - ширина среза; - угол сдвига.

(1.2) (1.3)

Допускаем, что к модели процесса резания с одной плоскостью сдвига применим принцип минимума затрат энергии. (1.4) (1.5)

Данному условию соответствует только одно единственное значение угла

Анализ полученного соотношения показывает, что угол сдвига будет уменьшаться

А с увеличением переднего угла угол сдвига будет увеличиваться.

Теоретические основы разработки модели процесса резания с развитой зоной пластической деформации веерообразной формы.

М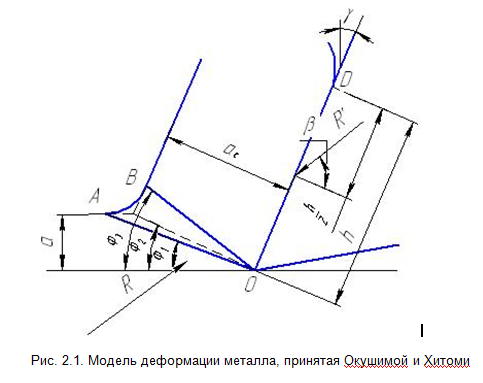 одель процесса резания с развитой зоной пластической деформации может описывать пластическую зону с веерообразной (треугольной) формой и с параллельными границами.

Рассмотрим модель с веерообразной формой пластической зоны предложенной, исследователями Окушимой и Хитоми. Форма зоны деформации иллюстрируется рис. 2.1.

Аналитическое исследование выполнено на основе изменения геометрии, граничных линий зоны пластической деформации.

Предполагалось, что материал идеально пластичен и касательные напряжения по линиям ОА, ОВ, ОD равны напряжениям течения материала при сдвиге.

Таким образом:

(2.1)

Исходя из условий равновесия,

(2.2)

(2.3) (2.4)

где b – ширина среза; h – длина площадки контакта стружки с инструментом.

Из уравнений (2.1) и (2.4) были выражены были выражены углы Ф₁, Ф₂:

(2.5) (2.6)

где (2.7)

и (2.8)

при и

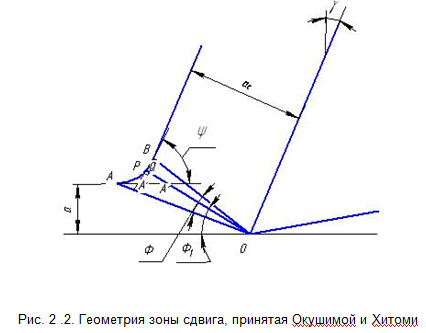
Размеры зоны деформации представлены углом Ф:

(2.9)

В последней экспериментальной работе были определены приблизительные значения h₁ и h₂ (h₁≈2, h₂≈1). Таким образом, значения B₁ и B₂ могут быть определены, если известны углы γ и β. Следовательно, может быть определена и толщина зоны деформации.

Деформация сдвига была определена из геометрических соображений, как показано на рис. 2. Таким образом, . (2.10)

в точке А, ψ=0, поэтому Г_А=0, в точке В (2.11)

Эта модель предполагает увеличение деформации материала при прохождении через зону сдвига.

Теоретические основы разработки процесса резания с развитой зоной пластической деформации с параллельными границами.

С целью упрощения математических выкладок при определении размеров пластической зоны с параллельными границами допускаем, что упрочнения материала проявляется только после пересечения границы А₂B₂ (рис.3.1.).

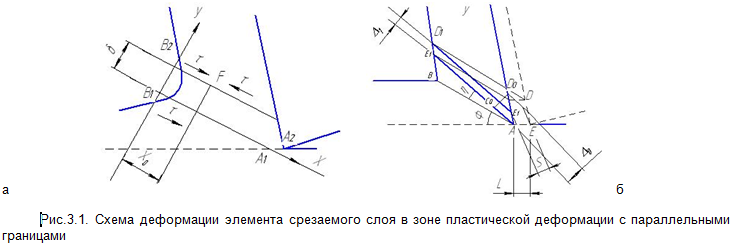
В основу расчетного метода положим равенство давления, действующего по нормали к границе переходной пластически деформированной зоны со стороны образующейся стружки, давлению, которое может передавать обрабатываемый материал, заключенный между границами этой зоны.

В соответствии с результатами, полученными исследователями Т.Н. Лопадзе, Н.В.Талантова и других исследователей, зону, определяющую формоизменение срезаемого слоя принимаем ограниченной плоскостями параллельными условной плоскости сдвига.

В процессе резания обрабатываемый материал, находящийся вне зоны пластической деформации, движется по отношению к режущему инструменту со скоростью υ. Для принятой жесткопластической схемы деформации, в системе координат ХОY эта часть материала может рассматриваться как абсолютно жесткое тело, пластически деформирующее переходную зону стружкообразования со скоростями υ_x и υ_y.

Для определения значений υ_x и υ_y рассмотрим переход произвольного элемента срезаемого слоя ACDE в элемент стружки AC₁D₁E₁ как результат одновременного сжатия сдвига и поворота в плоскости XOY (рис. 3.1, б). Поскольку величина поворота элемента срезаемого слоя не оказывает влияния на его формоизменение, то анализ деформации этого элемента проводим в предварительно повернутом положении AC₀D₀E₀.

За время перемещения резца из точки Е в точку А элемент срезаемого слоя толщиной Δ₀ сжимается до толщины Δ₁ и сдвигается на величину S. Следовательно, имеет место следующее соотношение:

, (3.1), где υ_сж, υ_сд – скорости сжатия и сдвига рассматриваемого элемента при переходе его из AC₀D₀E₀ в элемент стружки AC₁D₁E₁.

Проекция вектора скорости на ось Х и вектора скорости сжатия на ось Y соответственно равны значениям υ_x и υ_y:

Здесь учтено, что (3.2)

В процессе сжатия на границе А₂В₂ пластически деформируемого элемента срезаемого слоя вектор скорости перемещения любой материальной точки вдоль оси Х совпадает с направлением вектора скорости сдвига и по величине может быть либо больше, либо меньше его. Точка F, в которой скорость перемещения деформируемого материала по отношению к скорости сдвига равна нулю, является нейтральной. По обе стороны от точки F касательные напряжения имеют противоположное направление: на участке B₂F вдоль оси X, а на участке FA₂ противоположно оси X.

На границе с недеформированным срезаемым слоем вектор скорости перемещения любой материальной точки направлен противоположно вектору сдвига . Поэтому независимо от соотношения скорости перемещения материала вдоль оси X деформируемого под действием сжатия, и скорости сдвига касательные напряжения не меняют знака по всей границе A₁B₁ и направлены вдоль оси X.

Дифференциальные уравнения равновесия для плоско-деформированного состояния, условие пластичности и дифференциальные уравнения скоростей перемещений имеют вид:

(3.3),

где – составляющая тензора напряжений; - предел прочности обрабатываемого материала на сдвиг; , - составляющие скорости перемещения материальных точек деформируемого элемента.

Если принять, что в направлении оси X касательные напряжения могут изменять только знак, оставаясь постоянными по абсолютной величине, то из системы уравнений (3.3) следует:

(3.4)

Примем, что вдоль плоскости A₁B₁ а по границе со стружкой A₂B₂

где А – параметр, характеризующий изменение напряжения в материале в результате потери его сплошности.

(3.5)

где - вязкость разрушения при плоском деформированном состоянии; - толщина среза, м; - скорость резания, м/с; - предел прочности обрабатываемого материала на срез, МПа; – плотность обрабатываемого материала, МПа с²/м².

Т.о., допускаем наличие несплошности в деформируемой зоне по границе со стружкой.

Используя граничные условия y = 0, и для определения постоянных C₁ и C₂ в уравнении (3.4) и решая систему уравнений (3.3) получим:

(3.6)

Подставим значение , в уравнение пластичности:

Это тождество удовлетворяется, если

(3.8)

Знак минус перед коэффициентом A и индекс 3 при постоянной интегрирования относятся к участку B₂F, а знак плюс и индекс 4 – к участку FA₂.

С учетом соотношений (3.8) уравнения (3.6) преобразуется к виду:

(3,9)

Постоянные интегрирования C₃ и C₄ определим из граничных условий. На свободной поверхности стружки напряжения равны нулю. Удовлетворив краевое условие при найдем В силу неразрывности напряжений в точке P имеем: , (3.10)

где – абсцисса нейтральной точки F.

Положение нейтральной точки F определим из условия равновесия скорости сдвига и скорости перемещения точек деформируемого элемента вдоль оси X под действием сжатия. Выражения для скоростей перемещений, удовлетворяющие уравнениям (3.3) имеют вид:

(3.11)

Для определения постоянной С₅ воспользуемся условием равенства потока материала деформируемого элемента, проходящего через сечение количеству выдавливаемого материала на длине при его сжатии со скоростью , (3.12), где - толщина среза.

Решая уравнение (3.12) получим:

. (3.13)

Приравнивая скорость перемещения материальных частиц на поверхности A₂B₂ ( к скорости сдвига определим:

Подставляя соотношение (3.11), (3.13) и (3.14)в уравнение (3.9)и интегрируя по X в интервале от 0 до , запишем полученный результат относительно толщины пластически деформированного слоя:

где P – давление, действующее на деформированный слой по нормали к плоскости сдвига.

Для определения нормального давления, действующего на пластически деформированную зону, воспользуемся формулой для определения гидростатического давления [1]. С учетом гидростатического давления, действующего по границе деформированной зоны, выражение (3.15) примет вид:

где

В частности, для элементной стружки A = 0 и формула (3.16) упрощается:

(3.17)

Для сливной стружки А =1 и следовательно, , т.е. получаем модель с одной плоскостью сдвига.

Ввиду того, что зависимость близка к линейной величину можно определить приближенно:

(3.18)