4. Тепловые явления при резании металлов

Механическая энергия, расходуемая на процесс резания, в основном превращается в теплоту. Теплообразование оказывает двойное воздействие на резание. С одной стороны, интенсивное тепловыделение облегчает деформирование материала срезаемого слоя, способствует образованию промежуточного (окисленного) слоя на контактных поверхностях стружки и заготовки, что приводит к уменьшению износа инструмента, увеличению его стойкости, повышению качества обработанной поверхности и производительности. С другой стороны, повышение температуры в зоне резания до 800…1000оС может привести к отпуску материала инструмента и разупрочнить резец, что приводит к его интенсивному изнашиванию. Кроме того, теплота может стать причиной изменения действительных размеров детали вследствие увеличения размеров инструмента до 0,03…0,04 мм.

Почти вся механическая энергия при резании переходит в тепловую и только небольшая часть накапливается в поверхностном слое заготовки в виде потенциальной энергии искаженной решетки материала.

5. Износ инструмента

Износ режущего инструмента включает следующие меха­низмы: абразивный, адгезионный (молекулярный), диффузионный, окислительный, тепловой.

Абразивный износ происходит в результате царапания ма­териала инструмента твердыми структурными составляющими об­рабатываемого металла (этому способствует наличие окалины и литейной корки на заготовке).

Адгезионный (молекулярный) происходит путем вырывания частиц на передней поверхности инструмента вследствие схваты­вания контактных поверхностей стружки и резца. Процесс протека­ет на молекулярном уровне.

Диффузионный износ происходит в результате растворения материала инструмента в обрабатываемом материале. Процесс протекает на атомном уровне. При этом происходит диффузия не молекул химического соединения, а атомов отдельных элементов (например, С, W, Ti, Co и др.) В частности, диффузия углерода мате­риала инструмента в обрабатываемый материал приводит к обезуг­лероживанию рабочих поверхностей инструмента и этим ускоряет износ. Диффузионный износ наблюдается при высоких скоростях ре­зания, когда температура резания превышает 900-1000°С.

Окислительный износ происходит в результате окисления рабочей поверхности инструмента. Прочность окислов, как прави­ло, ниже прочности основного материала инструмента, что спо­собствует его поверхностному разрушению при взаимодействии с обрабатываемым материалом.

Тепловой износ является следствием повторяющихся воздей­ствий нагрева и охлаждения инструмента. Образующиеся при этом термические напряжения вызывают образование мелких трещин на поверхности инструмента, которые облегчают разрушение его по­верхности при взаимодействии со стружкой или поверхностью дета­ли. Тепловой износ характерен для прерывистого процесса резания.

2. Основные аспекты математического моделирования процесса резания

Аналитическое исследование напряженно-деформированного состояния срезаемого слоя, прямо или косвенно сводится к использованию элементов теории пластичности. Основу теории пластичности составляет теория напряжений, теория деформаций и уравнения связи между напряжениями и деформациями. Теория напряжений описывает статическое состояние процесса. Напряженное состояние в любой точке описывается тензором напряжений:

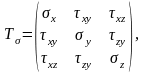(1.1)

где х, у, z – нормальные напряжения;

ху, xz, zy – касательные напряжения.

В тех случаях, когда инерционные составляющие напряжений являются малыми величинами, уравнения равновесия, составленные из компонентов тензора напряжений, имеют вид:

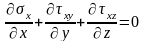
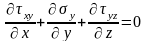(1.2)

Эти уравнения равновесия являются справедливыми и для условий пластической деформации в процессе резания. Расчеты показывают, что в типичных условиях обработки материалов резанием инерционные напряжения не превышают 0,015...0,3 МПа. Вследствие малости инерционных напряжений, их влиянием на условия равновесия (1.2) в теории резания пренебрегают.

Теория деформации описывает кинематическое состояние процесса. Деформационное состояние описывается тензором скоростей деформаций:

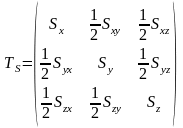, (1.3)

где Sх, Sу, Sz – нормальные компоненты скорости деформаций;

Sху, Syz, Szx – компоненты скорости деформаций сдвига.

Связь между компонентами скорости перемещения частицы сплошной среды и = и (х, у, z),  =  (х, у, z), w = w (х, у, z) и компонентами скорости деформаций определяется соотношениями:

, ,

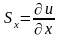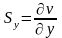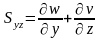, , (1.4)

, .

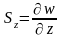Теория напряжений и теория деформаций описывают раздельно статическое и кинематическое состояние процесса деформации. Связь между этими теориями описывается уравнениями состояния или физическими уравнениями.

Критерием перехода в пластическое состояние являются условия текучести Треска-Сен-Венана или Мизеса. Согласно первому условию, пластическое течение начинается при достижении разностью максимального и минимального главных напряжений 1 и 3 удвоенного значения предела текучести материала на сдвиг

1 - 3 = 2S, (1.5)

Большее соответствие опытным данным дает условие Мизеса, согласно которому пластическое течение наступает при достижении интенсивностью касательных напряжений предела текучести материала на сдвиг

, (1.6)

В теории резания известно использование условия пластичности Треска-Сен-Венана и условия пластичности Мизеса.

Используя граничные условия, авторы получали полные и замкнутые решения. В связи с математическими сложностями прямое интегрирование уравнений, описывающих пластическое течение, удается осуществить лишь в простейших условиях. Стремясь упростить математические выкладки, многие исследователи использовали упрощенные методы решений, основанные на ряде гипотез и допущений, разработанные в прикладных задачах теории пластичности:

- метод характеристик или метод линий скольжения. Этот метод применим в основном к плоским задачам. Система дифференциальных уравнений для этого класса задач относится к гиперболическому типу и имеет два семейства ортогональных характеристик, совпадающих с линиями скольжения. Решение сводится к построению сетки линий скольжения и использованию их свойств. Напряжения и скорости находятся последовательно. Применение метода линий скольжения позволило получить целый ряд важных с теоретической и практической точек зрения решений в области механики процесса резания материалов.

- расчетные методы, основанные на экстремальных принципах теории пластичности. В соответствии с этими принципами мощность, вычисленная на основе статически допускаемого поля напряжений, является нижней оценкой, а мощность, вычисленная на основе кинематически возможного поля скоростей, является верхней оценкой истинной мощности, развиваемой в зоне деформации.

- в методе нижней оценки поле напряжений удовлетворяет уравнениям равновесия, условию пластичности, граничным условиям для напряжений. Метод верхней оценки требует, чтобы поле скоростей удовлетворяло условию несжимаемости среды и граничным условиям для скоростей и перемещений.

- метод верхней оценки в теории резания используется преимущественно в виде гипотезы о минимуме мощности стружкообразования. Задачи решены исходя из разрывных полей скоростей. Это является определенной схематизацией процесса резания, но при этом получаются простые в математическом отношении зависимости, например, для угла сдвига, усадки стружки, усилий резания и др.

- теория функции комплексного переменного, для построения кинематически возможных полей скоростей перемещений. При этом действительное поле скоростей аппроксимировано в исследуемой области зоны резания кинематически возможным безвихревым полем с помощью аналитической функции – комплексного потенциала. Комплексный потенциал является функцией, которая осуществляет конформное отображение зоны резания на каноническую область – полосу в плоскости потенциала. Решение задач, связанных с пластическим течением материала при стружкообразовании, приводит к сложным вычислениям, требующих определения, а также вычисления некоторых интегралов по каноническим областям.

Рассмотренные методы теории пластичности основаны на принципах механики сплошной среды и поэтому использовались в основном при решении задач для сливного стружкообразования. В тех случаях, когда процесс стружкообразования протекает с нарушением сплошности структуры на решение задач накладываются дополнительные условия и ограничения. Трудность при этом заключается в отыскании таких ограничений чтобы задача по определению неизвестных параметров была корректной. Этим объясняется, по-видимому тот факт, что применение методов теории пластичности к анализу элементного стружкообразования является очень ограниченным.

Основной механизм процесса резания обычно изучают на модели с одной режущей кромкой, расположенной перпендикулярно вектору скорости относительного перемещения инструмента и заготовки.

Впервые схему процесса стружкообразования предложил И.А. Тиме в 1870 г. [187], которая в дальнейшем получила развитие в работе К.А. Зворыкина [55] (рис. 1.1.).

В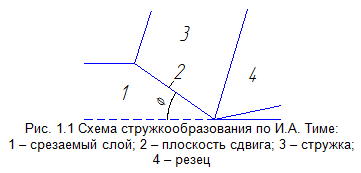 соответствии с этой моделью предполагается, что переход срезаемого слоя в стружку происходит в результате сдвиговых деформаций по единственной плоскости, проходящей от режущей кромки к свободной поверхности срезаемого слоя. По обе стороны от этой плоскости деформация отсутствует.

Основными недостатками модели с единственной плоскостью сдвига являются разрыв напряжений и скоростей перемещения частиц металла в плоскости сдвига и невозможность аналитического определения скорости деформации при стружкообразовании.

На основании ктритического анализа этой модели А.А. Брикс и впоследствии Н.Н. Зорев отмечают, что более обоснованно предполагать существование некоторой переходной пластически деформированной зоны, разделяющей обрабатываемый материал и образовавшуюся стружку. Схемы, учитывающие деформацию материала в некотором объеме, получили название – схемы стружкообразования с развитой зоной пластической деформации.

Н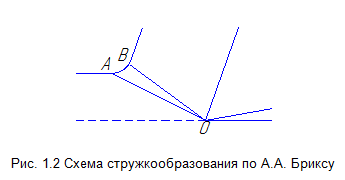 аиболее простая схема, учитывающая конечные размеры зоны деформации, впервые предложена А.А. Бриксом (рис. 1.2).

А.А. Брикс высказал предположение, что пластические сдвиги в срезаемом слое происходят по семейству плоскостей, расположенных веерообразно и расходящихся от режущей кромки (из точки 0). В точке В наружная поверхность стружки претерпевает излом. Наличие такого излома приводит к разрыву напряжений и скоростей перемещения частиц материала в этой точке. Кроме того, как отмечает в работе [58] Н.Н. Зорев, схема А.А. Брикса не удовлетворяет условиям выхода линий скольжения на свободную поверхность.

Н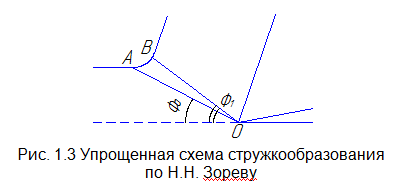 .Н. Зорев рассмотрел упрощенную схему стружкообразования с веерообразной переходной пластически деформированной зоной отличающуюся от схемы А.А. Брикса наличием плавного споряжения в точке В (рис. 1.3).

Такую же схему позднее рассматривали японские исследователи К. Окушима и К. Хитоми. Нетрудно заметить, что применение такой схемы стружкообразования приводит к неопределенности задачи в области режущей кромки.

В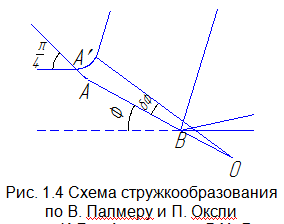 .Б. Палмер и П.Б. Оксли исключили эту неопределенность, поместив центр веера линий скольжения на некотором расстоянии от режущей кромки (рис. 1.4). Кроме того, авторы использовали криволинейный контур зоны пластической деформации вблизи свободной поверхности для соблюдения условия выхода линий скольжения.

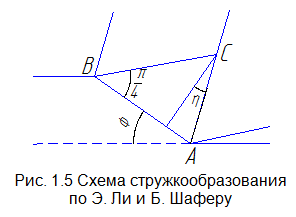
Э. Ли и Б. Шафер предложили гипотезу, в которой предполагается, что стружка напряжена до предела тякучести в треугольной зоне, прилегающей к плоскости сдвига АВ (рис. 1.5), но деформация остается при этом простым сдвигом вдоль АВ. Трение стружки по передней поверхности режущего инструмента определяется углом .

Анализируя поле линий скольжения, соответствующее принятой схеме стружкообразования Э.Ли и Б. Шаффера, справедливо отмечено, что в области, примыкающей к свободной поверхности стружки, оно мало достоверно и может быть использовано лишь в той мере, в какой это делается в настоящее время при решении задач с применением метода верхних оценок.

С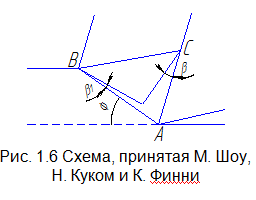 хему стружкообразования Э.Х. Ли и Б.В. Шаффера усовершенствовали М.К. Шоу, Н.Г. Кук, И. Финни [244]. Ими было сделано предположение, что плоскость сдвига не является плоскостью максимальных касательных напряжений и линия скольжения не совпадает с плоскостью сдвига (рис. 1.6).

Н аиболее слабым местом в данной теории стружкообразования, является предположение, об отклонении направления деформации сдвига от направления максимального усилия сдвига. Кроме того, авторы не дают никаких сведений о величине угла ₁.

Некоторые исследователи стремясь учесть размеры зоны пластической деформации ограничивали ее параллельными линиями. Н.В. Талантов , С. Спанс приводят экспериментальные доказательства параллельности границ зоны деформации В.И. Садчиков и В.С. Кушнер показывают, что схемы стружкообразования с зоной пластической деформации ограниченной параллельными линиями удовлетворяют условиям сплошности и непрерывности деформируемой среды.

Типичные схемы стружкообразования, пластическая деформация в которых происходит в зоне с параллельными границами, приведены на рис. 1.10. В приведенных схемах границы стружкообразования располагаются по обе стороны от условной плоскости сдвига. Такие схемы стружкообразования использовали в своих работах Т.Н. Лоладзе, Н.В. Талантов, В.С. Кушнер, Д.Б. Оксли, и др.