4.3. Обратный оператор

Определение 1. Пусть и линейные пространства. Линейный оператор называется обратимым, если уравнение имеет единственное решение. Совокупность всех векторов , для каждого из которых существует вектор , такой, что , называется образом оператора A (множеством значений оператора A) и обозначается или .

Комментарий. Множество Im(A) значений оператора A может, вообще говоря, и не совпадать со всем пространством .

Определение 2. Совокупность всех векторов , на которых оператор A определён, называется областью определения оператора A и обозначается или .

Определение 3. Если оператор A обратим, то каждому вектору 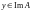сопоставляется единственный вектор , являющийся решением уравнения . Оператор, осуществляющий это соответствие, называется обратным к A и обозначается .

Если существует обратный оператор , то решение задачи записывается в явном виде: . То есть необходимо найти элемент , если задан элемент . Ясно, что важное значение приобретает выявление условий, при которых обратный оператор существует и ограничен.

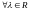
Комментарий. Множество , где Е линейное пространство, называется линейным многообразием, если и , то есть содержит все линейные комбинации входящих в него векторов. В линейной алгебре чаще используют термин “линейное подпространство”. Множество , где x₀ ∈ E, L — линейное многообразие, называется аффинным многообразием. В частности, M является линейным подпространством тогда и только тогда, когда М содержит нулевой элемент. Множество значений оператора есть линейное многообразие в . В самом деле, пусть и .Тогда найдутся векторы ,такие, что Ax₁=y₁ и Ax₂=y₂. Поэтому для любых чисел верно, что , то есть вектор . Ясно, что .

Теорема 1 . Пусть оператор линеен и существует . Тогда тоже линеен. Для произвольных обозначим . Тогда Теперь .

Определение 4. Ядром оператора называется множество . Очевидно, что не пусто, так как .

Определение 5. Оператор называется вырожденным, если .

Теорема 2. Пусть и линейные конечномерные пространства, а оператор линейный. Обратный оператор существует тогда и только тогда, когда оператор невырожденный.

Достаточность. Пусть оператор невырожденный, т.е. (нуль-пространство, ядро оператора тривиально). Тогда для любых двух элементов имеем , то есть оператор взаимно однозначный, а значит, существует обратный оператор .

_{Необходимость}. Пусть оператор имеет обратный оператор . Заметим, что линейный оператор (теорема 1) и докажем что невырожденный. Пусть это не так, то есть существует такой, что 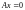. Тогда . Полученное противоречие показывает, что , то есть оператор невырожденный.

Комментарий. В доказательстве теоремы не участвует размерность пространства. Однако, она верна только в конечномерном случае, то есть в конечномерном пространстве оператор обратим, если и только если . В бесконечномерном пространстве это, вообще говоря, не так. Например, множество всех ограниченных последовательностей с операциями покоординатного сложения и умножения на скаляр образует линейное пространство. Определим на нём оператор сдвига . Ясно, что ( 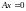только при ). Однако этот оператор не имеет обратного. В самом деле, пусть оператор существует и . Рассмотрим вектор . Тогда . Но первая координата вектора всегда равна нулю, а должна быть единица.

Нас интересует не только разрешимость уравнения , но и непрерывная зависимость решения от правой части уравнения, то есть корректность уравнения. Теорема 3. Критерий непрерывности обратного оператора. Пусть и линейные нормированные пространства. Оператор существует и непрерывен на если и только если и выполняется неравенство . . Необходимость. Пусть обратный оператор существует и ограничен на . Тогда существует такая постоянная , что . Обозначая и , сразу получаем .

Достаточность. Из того, что следует, что уравнение имеет единственное решение . В самом деле, пусть . Тогда , то есть , то есть . Тогда из теоремы 2 следует существование обратного оператора . Полагая в этом неравенстве , сразу получим .

Определение 6. Пусть и линейные нормированные пространства Оператор А называется непрерывно обратимым, если , причём , .

Определение 7. Задача решения уравнения корректно разрешима по Адамару, если

1. Уравнение имеет единственное решение для любой правой части у;

2. Решение 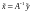того же уравнения с возмущённой правой частью таково, что . Это означает, что малое изменение правой части y влечет малое изменение решения.

Комментарий. Если линейный оператор А непрерывно обратим, то задача решения уравнения корректно разрешима по Адамару.

В случае существования непрерывного оператора имеет место следующая теорема:

Теорема 4. (теорема Банаха о гомеоморфизме.) Пусть , где –биективный непрерывный линейный оператор, банаховы пространства и , то существует линейный непрерывный обратный оператор . Из биективности отображения следует однозначная разрешимость уравнения для любой правой части, то есть существование обратного оператора . Его линейность следует из теоремы 1. Непрерывность же обратного оператора следует из принципа открытых отображений Банаха: оператор , как непрерывный оператор, любое открытое множество переводит в открытое. Тогда для оператора его прообраз открыт. Тогда, в соответствии с критерием непрерывности, оператор непрерывен.

Таким образом, если – биективный непрерывный линейный оператор, такой, что , где - банаховы пространства, и , то задача решения уравнения корректно разрешима по Адамару.