IV. Пространства операторов

4. 1. Определение линейного оператора

Пусть X и Y –нормированные пространства, оба вещественные или оба комплексные или линейные топологические пространства.

Определение 1. Линейным оператором, действующим из пространства X в пространство Y называется отображение или или (если ,где и пространства функций), удовлетворяющее условию , где .

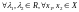Пример 1. Пусть по правилу , то есть оператор I переводит каждый вектор пространства X в себя. Ясно, что . Это единичный оператор. Соответственно, нулевой оператор переводит каждый вектор пространства в нулевой вектор пространства .

Комментарий. Единичный оператор иногда обозначают буквой . Это те, кто считает, что слово единица пишется через “E”. Символ 0 теперь может означать либо число нуль, либо нулевой вектор пространства , либо нулевой вектор пространства , либо нулевой оператор, действующий из пространства в пространство .

Пример 2. Пусть конечномерные эвклидовы пространства, базис в пространстве а базис в пространстве . Тогда верно, что . Оператор A линеен, то есть . Но каждый из векторов лежит в пространстве и поэтому может быть разложен по базису : . Тогда . Совокупность чисел называется матрицей оператора A. Совокупность чисел называется матрицей оператора A. То есть каждому оператору соответствует некоторая матрица и наоборот, каждой матрице соответствует некоторый линейный оператор A. Поскольку векторы линейно независимы, то коэффициенты при векторе в левой и правой частях последней формулы должны совпадать, то есть , или .

Определение 2. Оператор А ограничен, если для любых x  X, справедлива оценка , где с – постоянная. Точная нижняя грань всех таких констант с на называется нормой оператора А и обозначается .

Комментарий. По определению, , то есть норма во первых, одна из верхних граней, а во вторых , что означает несдвигаемость верхней грани.

Теорема 1. Обозначим , , . Покажем, что . Так как 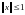, то . Тогда . С другой стороны из несдвигаемости верхней грани следует, что . Рассмотрим элемент . Тогда для него . Но норма 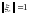, поэтому . В силу произвольности , сразу получаем . Таким образом . Но одновременно , то есть .

Покажем теперь, что выполняются и остальные равенства. Для этого докажем, что . Первое неравенство очевидно, поскольку в обеих его частях супремум берется от одной и той же величины . Второе неравенство следует из того, что для любого .

Третье неравенство следует из того, что для любого и имеем .

Комментарий. Для числовых функций линейная функция всегда ограничена. В конечномерных пространствах любой линейный оператор является ограниченным. Для линейного оператора в бесконечномерных пространствах это, вообще говоря, не так.

Пример 3. Оператор дифференцирования. Рассмотрим операторное уравнение в пространствах . Пусть оператор дифференцирования 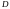действует из в , то есть оператор . Этот оператор определен не на всем пространстве непрерывных функций, а лишь на подпространстве непрерывных функций, имеющих непрерывную производную. В пространстве норма . Достаточно указать один элемент пространства, для которого ограниченность не имеет места. Возьмем из последовательность х_n(t) = tⁿ. Она ограничена в : . Рассмотрим = = .Тогда норма . Таким образом, оператор переводит ограниченное множество в неограниченное, то есть этот оператор не является ограниченным. Такая же ситуация с последовательностью . В норма , а . Тогда при тоже стремится к бесконечности, то есть оператор дифференцирования А неограничен, то есть не является непрерывным. Но если в пространстве исходных данных Х выбрать более сильную норму, то ситуация изменится. Рассмотрим пространство Х как пространство а пространство У как пространство С[a,b]. Тогда Теперь

Пример. Линейный функционал в в точках (1,2) и (3,4) равен 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.

_{Пример.} Значение линейного функционала в в точке (1,1) равно , а его норма равна . Найти его значение в точке (7,8). Линейный функционал, заданный на плоскости, имеет вид , то есть это плоскость, проходящая через начало координат. Его норма – это максимальное значение этой функции на единичном шаре в . Таким образом, имеем симметрическую СЛАУ

Пример. Значение линейного функционала в в точке (1,1) равно , а его норма равна . Найти его значение в точке (7,8).

Комментарий. Из геометрического смысла понятия нормы видно, что общий вид линейного функционала в пространствах задаётся формулой , где . Нормы же их определяются выражениями _.

Пример. Рассмотрим преобразование двумерного пространства 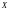в двумерное пространство оператором , причём матрица линейного оператора невырождена и имеет вид .

1. Рассмотрим преобразование , где точки , а точки . Тогда , а . Обозначим . Тогда . Запишем это как скалярное произведение и воспользуемся неравенством Буняковского Коши.

. Тогда

, то есть а норма называется эвклидовой.

2. Рассмотрим преобразование .

. Такая норма называется столбиковой.

3. Рассмотрим преобразование .

Тогда

Такая норма называется строчной.