22. Закон розподілу випадкової величини.

Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.

Закон розподілу можна задавати таблицею, формулою, графіком.

У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:

Х = хі	х1	х2	х3	......	хk
Р(Х = хі) = рі	р1	р2	р3	.....	рk

Оскільки випадкові події (Х = х_j) і (Х = х_m) є між собою несумісними (Х = х_і) ∩ (Х = х_m) = , то - умова нормування для дискретної випадкової величини Х. Закон розподілу таблицею називають рядом розподілу.

23. Інтегральна функція розподілу випадкової величини: означення. Властивості.

Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(х), так звану інтегральну функцію.

Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей: F(x) = P(X < x) - унаслідок експерименту випадкова величина може набути значення, меншого за х .

Розглянемо властивості F(x):

1.

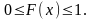
2. 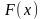 є неспадною функцією, а саме 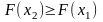, якщо .

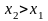24. Диференціальна функція розподілу (щільність розподілу) випадкової величини: означення. Властивості.

Для неперервних випадкових величин закон розподілу ймовірностей зручно описувати з допомогою щільності ймовірностей, яку позначають f (x).

Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):

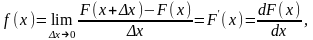звідки

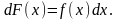
Оскільки 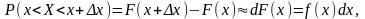то добуток f (x) dx — ймовірність того, що випадкова величина Х міститиметься у проміжку [х, х + dx], де .

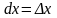Геометрично на графіку щільності ймовірності f (x) dx відповідає площа прямокутника з основою dx і висотою f (x).

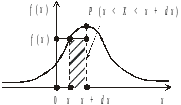
Властивості f (x)

1. . Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.

2. Умова нормування неперервної випадкової величини Х:

Якщо НВВ Х належить [a; b], то умовою нормування буде

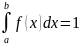
3. Імовірність попадання неперервної випадкової величини в інтервалі обчислюється за формулою

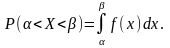
4. Функція розподілу ймовірностей неперервної випадкової величини має вигляд

25. Математичне сподівання випадкової величини: означення, властивості.

Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання.

Термін «математичне сподівання» випадкової величини Х є синонімом терміна «середнє значення» випадкової величини X.

Математичним сподіванням випадкової величини Х, визначеною на дискретному просторі Ω, називається величина

Якщо Ω — обмежена множина, то .

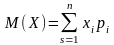Якщо простір Ω є неперервним, то математичним сподіванням неперервної випадкової величини Х називається величина

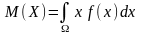
Якщо Ω = (– ; ), то

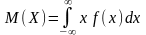
Якщо Ω = [a; b], то

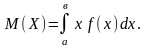
Властивості математичного сподівання

1. Математичне сподівання від сталої величини С дорівнює самій сталій: М (С) = С.

2. М (СХ) = СМ (Х).

Для дискретної випадкової величини згідно із маємо .

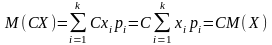Для неперервної:

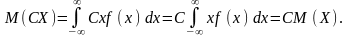
3. Якщо А і В є сталими величинами, то .

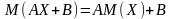Для дискретної випадкової величини: .

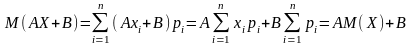Для неперервної випадкової величини: