- •Означення та приклади подій: випадкова, достовірна, неможлива, елементарна, складна.
- •Означення та приклад повної групи подій та простору елементарних подій.
- •Класичне означення ймовірності випадкової події.
- •Сформулювати аксіоми класичної теорії ймовірностей.
- •Дати означення та вказати властивості перестановки, сполучення, комбінації елементів.
- •Дати означення відносної частоти появи події.
- •Дати геометричне та статистичне означення ймовірності.
- •Дати визначення умовної ймовірності.
- •Формула множення ймовірностей для залежних та незалежних подій.
- •Формула для обчислення появи хоча б однієї події .
- •Формула повної ймовірності.
- •Формули Байєса.
- •Означення експерименту за схемою Бернуллі.
- •Формула Бернуллі для обчислення ймовірностей, умова використання. Наслідки.
- •Найімовірніше число появ події в схемі Бернуллі.
- •Сформулювати локальну теорему Муавра-Лапласа.
- •Властивості функції Лапласа:
- •Означення випадкової величини, дискретної та неперервної випадкових величин.
- •Закон розподілу випадкової величини.
- •Інтегральна функція розподілу випадкової величини: означення. Властивості.
- •Диференціальна функція розподілу (щільність розподілу) випадкової величини: означення. Властивості.
- •Математичне сподівання випадкової величини: означення, властивості.
- •Дисперсія та середньоквадратичне відхилення випадкової величини: означення, властивості.
- •Властивості дисперсії
- •Мода, медіана випадкової величини.
- •Початкові та центральні моменти.
- •Асиметрія, ексцес.
- •Означення багатовимірної випадкової величини.
- •Означення закону розподілу багатовимірної випадкової величини.
- •Основні числові характеристики для системи двох дискретних випадкових величин.
- •Коефіцієнт кореляції та його властивості.
- •Функція розподілу ймовірностей та щільність ймовірностей системи
- •Двовимірний нормальний закон розподілу.
- •Закон розподілу Бернулі
- •Біноміальний закон розподілу двв. Числові характеристики.
- •Пуасонівський закон розподілу двв, числові характеристики.
- •Геометричний закон розподілу двв, числові характеристики.
- •Гіпергеометричний закон розподілу двв, числові характеристики.
- •Рівномірний закон розподілу нвв.
- •Нормальний закон розподілу.
- •Показниковий закон та його використання в теорії надійності та теорії черг.
- •Розподіл
- •Розподіл Стьюдента. Розподіл Фішера. (45-46)
- •Правило трьох сигм. Логарифмічний нормальний закон.
- •Функції одного дискретного випадкового аргументу.
- •.Числові характеристики функції одного дискретного випадкового аргументу.
- •Функції неперервного випадкового аргументу та їх числові характеристики.
- •Функції двох випадкових аргументів та їх числові характеристики.
- •Числові характеристики функції дискретного випадкового аргументу
- •Нерівності Чебишева та їх значення.
- •Теорема Чебишева.
- •Теорема Бернуллі.
- •Центральна гранична теорема теорії ймовірностей ( теорема Ляпунова) та її використання у математичній статистиці.
- •Предмет і задачі математичної статистики.
- •Утворення вибірки. Генеральна та вибіркова сукупність.
- •Статистичні розподіли вибірок.
- •Емпірична функція розподілу, гістограма та полігон.
- •Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.
- •Мода й медіана, емпіричні початкові та центральні моменти, асиметрія та ексцес.
- •Дати визначення статистичної оцінки.
- •Точкові та інтервальні статистичні оцінки.
- •Дати визначення довірчого інтервалу.
- •Що таке нульова та альтернативна статистичні гіпотези.
- •Перевірка (правдивості нульової) гіпотези про нормальний закон розподілу ознаки генеральної сукупності.
- •Емпіричні та теоретичні частоти.
- •Критерії узгодження Пірсона та Колмогорова.
- •Помилки першого та другого роду.
- •Статистичний критерій. Критична область.
- •Дати означення моделі експерименту.
- •Дати поняття одно факторний аналіз.
- •Загальна дисперсія, між групова та внутрішньогрупова дисперсії.
- •. Поняття про функціональну, статистичну та кореляційну залежності.
- •Рівняння лінійної регресії. Довірчий інтервал для лінії регресії
- •Вибірковий коефіцієнт кореляції.
- •Множинна регресія, множинний коефіцієнт кореляції та його властивості.
- •Нелінійна регресія.
- •85) Визначення та приклади ланцюгів Маркова.
- •Інтуїтивне визначення
- •Формальне визначення
- •Граф переходів ланцюга Маркова
- •86) Ймовірність переходу за n кроків.
- •87) Замкнуті множини станів.
- •88) Класифікація станів. Неповоротний стан.
- •1. Ергодичний стан
- •2. Нестійкі стани
- •3. Поглинальні стани
- •89) Ергодична властивість неперіодичних ланцюгів. Стаціонарний розподіл.
- •90) Періодичні ланцюги.
- •91) Загальний марковський процес (Ланцюг Маркова з неперервним часом).
- •92) Гранична поведінка перехідних ймовірностей ланцюга Маркова.
- •93) Гілчастий процес.
- •94) Алгебраїчний підхід вивчення скінченних ланцюгів Маркова.
- •96) Випадковий проце, стаціонарний у широкому сенсі.
- •97) Аналіз кореляційної функції. Ергодичність.
- •100) Рівняння Колмогорова - Чепмена
Рівняння лінійної регресії. Довірчий інтервал для лінії регресії
Якщо дано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку економетричну модель, яка б найкраще описувала існуючу залежність. Одним з методів є лінійна регресія. Лінійна регресія передбачає побудову такої прямої лінії, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю пряму одержуємо значення прогнозу. Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає:
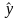 =а+bх, (1.1)
=а+bх, (1.1)
де - вирівняне значення у для відповідного значення х.
Константи а і b - константи, які передбачають зменшення суми квадратів відхилень між фактичним значенням у і вирівняним значенням .
(у - )2 min (1.2)
Коефіцієнт а характеризує точку перетину прямої регресії з лінією координат.
Коефіцієнт b характеризує кут нахилу цієї прямої до осі абсцис, а також на яку величину зміниться при зміні х на одиницю.
Коефіцієнти а і b знаходять із системи рівнянь (1.3), що випливає з формули (1.2).
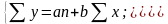 (1.3)
(1.3)
Знайшовши значення параметрів розраховують ряд вирівняних значень для відповідних факторів і проводять дослідження знайденої економетричної моделі.
Щоб зробити висновок про доцільність використання знайденої моделі проводять аналіз за наступними напрямками:
1) Розраховують критерій Фішера та перевіряють знайдену модель на адекватність вихідним даним;
2) Розраховують і аналізують дисперсію показників;
3) Розраховують і аналізують коефіцієнт кореляції;
4) Розраховують та аналізують коефіцієнт еластичності;
5) Розраховують довірчий інтервал для прогнозованих показників.
Довірчий інтервал.
Вихідна економетрична модель лінійної регресії передбачає наявність випадкової величини Е, яка вимірює похибку між фактичним значенням і вирівняним значенням показника. Для розрахунку цих похибок використовують поняття "стандартного відхилення"
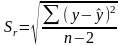 , (1.13)
, (1.13)
де Sr – стандартна похибка рівняння регресії
n-2 – число значень ряду зменшене на кількість параметрів рівняння регресії (тобто а і b).
Розрахувавши стандартну похибку рівняння регресії знаходимо стандартну похибку прогнозу:
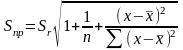 (1.14)
(1.14)
Для
розрахунку довірчих меж потрібно знайти
значення
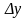 .
.
Нижня
межа довірчого інтервалу
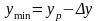 ;
верхня межа довірчого інтервалу
;
верхня межа довірчого інтервалу
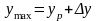 .
.
Прогнозне значення ур=a+bxp буде знаходитись в межах від уmin до ymax.
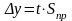 (1.15)
(1.15)
де t – критерій Стюдента (знаходиться з таблиць в залежності від ймовірності P і ступеня вільності n-m-1).
Вибірковий коефіцієнт кореляції.
Рівняння лінійної парної регресії:
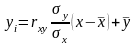 або
або
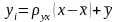 ,
,
де
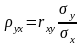 і називають коефіцієнтом
регресії.Для
обчислення
і називають коефіцієнтом
регресії.Для
обчислення
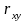 необхідно знайти
необхідно знайти
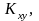
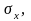
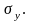
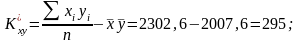
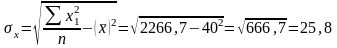 ;
;
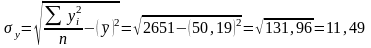 ;
;
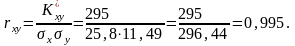
Як бачимо, коефіцієнт кореляції близький за своїм значенням до одиниці, що свідчить про те, що залежність між Х та Y є практично лінійною.
Множинна регресія, множинний коефіцієнт кореляції та його властивості.
Регресія (рос. регрессия, англ. regression; нім. Regression f) — форма зв'язку між випадковими величинами. Закон зміни математичного очікування однієї випадкової величини залежно від значень іншої. Розрізняють прямолінійну, криволінійну, ортогональну, параболічну та інші регресії, а також лінію і площину регресії.
Крива регресії Y на Х є залежність умовного математичного очікування величини Y від заданого значення Х:
my/x = φ (х, а, b, c, …),
де а, b, c, … — параметри рівняння регресії.
Регресія дозволяє за величиною однієї ознаки (змінна x) знаходити середні (очікувані) значення іншої ознаки (змінна У), зв'язаної з x кореляційно. Оскільки в дослідженнях конкретний вид взаємозв'язків невідомий, одне з головних завдань регресійного аналізу полягає у доборі відповідного виразу У = / (X), графік якого проходить через емпіричні точки (або досить близько до них) і таким чином зв'язує змінні x і У.
Множинна регресія - це оцінювання, наприклад, змінної У лінійною комбінацією т незалежних зміннихх1,х2, хт. Найпростіший варіант регресії має місце для т=2, коли необхідно спрогнозувати залежність однієї змінної У від двох змінних х1 і Х2. Рівняння такої множинної регресії має вигляд:
? = Бх ■ X! + Б2 ■ X2 + Б0,
де Б1 = Ь1 o Зу/^; Б2 = Ь2 ■ $у/$г;, Б0 = У - Ах■ X1 - А2 o X2;
Ь1 = (Гу1 ~ Гу2 o Г12 )/(1 - Г122 ) ; Ь2 = (Гу2 " Гу1 ' Г12 )/(1 " ^2 )
зу, з1, з2 , У, X1, X2 - стандартні відхилення і середні значення У , х1 і х2 ; Гу1, Гу2, г12 - коефіцієнти парної кореляції Пірсона між У і Х1, У і Х2, Х1 і Х2. Для оцінювання зв'язку, з одного боку, змінної У, а з іншого - двох змінних Х1 і Х2, використовують коефіцієнт множинної кореляції:
Ку-1,2 =д/Ь1 o Гу1 + Ь2 o Гу2 .
Множинний коефіцієнт кореляції
Множинний коефіцієнт кореляції визначається тоді, коли на дану ознаку
одночасно комплексно впливають дві інших ознаки (фактора) X i Z. В таких
випадках визначається не парний (по 2-х ознаках), а сукупний коефіцієнт
кореляції для 3-х ознак − X, Y, Z:
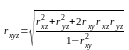
На відміну від парних коефіцієнтів кореляції сукупний коефіцієнт кореляції має лише позитивне значення.
Іноді необхідно при трьох взаємообумовлюючих факторах виявити взаємовплив лише для двох з них. Тоді застосовується коефіцієнт парціальної кореляції для обраних двох факторів (ознак). Це частинний (частковий) або парціальний коефіцієнт кореляції:
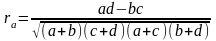
Відповідно