64. Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.

Аналогічно математичному сподіванню, дисперсії та середньоквадратичному відхиленню ДВВ визначають вибіркові характеристики замінюючи при цьому ймовірність р_к на відносні частоти .

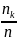Простим середньоарифметичним вибірки називають суму всіх варіант поділену на об’єм вибірки 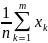, де n – об’єм вибірки, 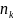- варіант вибірки, де к= .

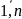Вибірковим середнім або зваженим середньоарифметичним вибірки назив середнє арифметичне варіант вибірки із врахуванням їх відносних частоті позначається вибіркове середнє: =

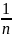
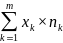
Вибіркове середнє аналогом математичного сподівання М(х) і використовується дуже часто, воно може приймати різні значення при різних вибірках однакового об’єму.

Основні властивості вибіркового середнього:

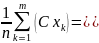
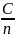
1. При множенні усіх варіант вибірки на однаковий множник, вибіркове середнє також множиться на цей множник = 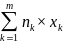= С

2. Якщо до усіх варіант вибірки додати (відняти) однакове число, то вибіркове середнє збільшується (зменшується) на це число

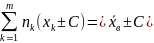
Вибірковою дисперсією Дв назив середнє квадратичне відхилення варіант від вибіркового середнього із врахуванням їх відносних частот

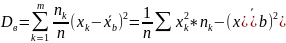
Вибірковим середньоквадратичним відхиленням назив квадратний корінь із вибіркової дисперсії, його ще назив стандартом:

Вибіркова дисперсія дає занижені значення для дисперсії генеральної сукупності.

Математичне сподівання вибіркової дисперсії

М(Dв) =

Тому вибіркову дисперсію доцільно виправити таким чином, щоб вона стала незміщеною оцінкою. Для цього достатньо Dв до множити на .

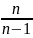Вибіркову дисперсію виправлену позначають ,

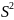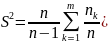
При великих об’ємах вибірки Dв і дисперсія генеральної сукупності мало відрізняються один від одного, тому виправлену дисперсію знаходять при об’ємах n<30.

65. Мода й медіана, емпіричні початкові та центральні моменти, асиметрія та ексцес.

Медіану вибірки позначають 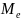. Якщо обсяг статистичного матеріалу є непарним числом, тобто n =2*k+1, де k – натуральне число, то медіана = .

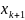Якщо обсяг статистичного матеріалу є парним числом, тобто m=2*k, де k – натуральне число. То медіаною вважають величину .

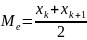Модою статистичного матеріалу назив той елемент цієї вибірки, який найчастіше трапляється у ній. Моду вибірки позначають . очевидно, що вибірка може мати кілька мод.

Початкові емпіричні моменти позначаються k=

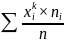
Якщо перший емпіричний момент, то матимемо 1=

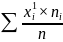
Відповідно, якщо другий, то 2=

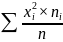
Центральний момент

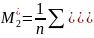
Третій та четвертий моменти застосовуються при знаходженні коефіцієнта асиметрії та ексцесу.

Асиметрія: 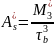Ексцес: 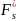= 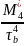- 3

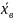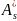Якщо варіант статистичного розподілу вибірки симетрично розміщені щодо вибіркового середнього , то в цьому випадку =0, оскільки 3 = 0.

При <0 варіант статистичного розподілу 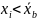переважають, то таку асиметрію назив додатною.

66. Дати визначення статистичної оцінки.

Статистичною оцінкою θ* невідомого параметра θ теоретичного розподілу називається його найближче значення, що залежить від вибірки. Статистична оцінка називається незсунутою, якщо математичне сподівання дорівнює самому параметру. Статистична оцінка називається зсунутою, якщо математичне сподівання не дорівнює параметру генеральної сукупності. θ* тим точніше визначає θ, чим менша абсолютна величина θ- θ*.