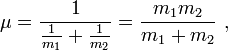8.Связь между потенциальной энергией и силой

Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы   , действующей на тело, и некоторое значение потенциальной энергии  U. Значит, между силой     и  U  должна быть связь   , с другой стороны,  dA = –dU, следовательно   , отсюда

Проекции вектора силы на оси координат:

Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор     направлен в сторону наибыстрейшего уменьшения U.

9. Потенциальная энергия силы упругости: .

Потенциальная энергия однородной силы тяжести: .

Потенциальная энергия гравитационного поля: .

Вопрос 5.

1.Механическая энергия.

Е сли тело может совершить механическую работу, то оно обладает механической энергией Е (Дж).  Существует два вида механической энергии: кинетическая и потенциальная.

Кинетическая энергия – энергия движущихся тел:

 Потенциальная энергия – энергия взаимодействующих тел: Е = mgh.

2.Виды механической энергии

К инетической энергией называют механическую энергию всякого свободно движущегося тела и измеряют ее той работой, которую могло бы совершить тело при его торможении до полной остановки.       Пусть тело В, движущееся со скоростью v, начинает взаимодействовать с другим телом С и при этом тормозится. Следовательно, тело В действует на тело С с некоторой силой F и на элементарном участке пути ds совершает работу По треть ему закону Ньютона на тело В одновременно действует сила -F, касательная составляющая которой -F_τ вызывает изменение численного значения скорости тела.

Итак, кинетическая энергия поступательно движущегося тела равна половине произведения массы этого тела на квадрат его скорости; кинетическая энергия тела не может быть отрицательной (E_k ≥ 0). Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.       Численно потенциальная энергия системы в данном ее положении равна работе, которую произведут действующие на систему силы при перемещении системы из этого положения в то, где потенциальная энергия условно принимается равной нулю (E_n = 0).

3 .Полная механическая энергия W системы равна сумме ее кинетической и потенциальной энергий:

4.Закон сохранения механической энергии

п олная механическая энергия частицы, движущейся в стационарном поле консервативных сил (т.е. при отсутствии сторонних сил) или в поле, где сторонние силы не совершают работы за исследуемый промежуток времени, остается постоянной:

5.Универсальный закон сохранения энергии: энергия никогда не создается и не уничтожается, она переходит из одной формы в другую или обменивается между отдельными частями материи (различные формы энергии: тепловая, химическая, ядерная и т.д.).

Вопрос 6.

1.Одномерное движение в потенциальном поле. Качественный анализ типов движений, устойчивости равновесных состояний.

Движение частицы в  потенциальном поле

 Полная энергия классической частицы

где W₀=mc² - энергия покоя частицы; W_k=p²/ 2m - кинетическая  энергия   частицы;  W_p(r) - потенциальная  энергия во внешнем силовом поле.

Вывод: Если  полная энергия частицы меньше значения ее потенциальной энергии (для удаленных областей пространства), то частица может проникать только в ограниченную область пространства - такое движение называют финитным.

Примером финитного движения является движение планет в Солнечной системе.

Такое  движение является весьма    устойчивым, поскольку Солнечная система существует около пяти миллиардов лет.

Если же частица может удаляться на неограниченное расстояние от системы отсчета, то такое движение называется инфинитным.

Пусть одномерная частица движется в потенциальном силовом поле вдоль оси Х зависимости потенциальной энергии силового поля W_p(x), от координаты х, которую называют "потенциальной ямой".

Частица всегда находится внутри "потенциальной ямы" - движение является финитным, кроме того, будет периодически повторяться, т.е. частица совершает колебательное периодическое движение.

W₁ = W_p(A) = mv² / 2 + W_p(A),

т.е. в точке поворота скорость частицы обращается в нуль.

Таким образом, границы движения классической частицы определяются значением полной энергии.

2.Задача двух тел. Приведенная масса. Сведение задачи двух тел к задаче об одном теле.

В классической механике, задача двух тел состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом.

Задачу двух тел можно представить как две независимых задачи одного тела, которые привлекают решение для движения одной частицы во внешнем потенциале.

Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной (например, электромеханической) системе, зависящая от физических параметров системы (масс, моментов инерции, индуктивности и др.) и от её закона движения.

Обычно приведенная масса   определяется из равенства  , где   — кинетическая энергия системы, а   — скорость той точки системы, к которой приводится масса. 

Задача двух тел

В задаче двух тел, возникающей, например, в небесной механике или теории рассеяния, приведённая масса появляется как некая эффективная масса, когда задачу двух тел сводят к двум задачам об одном теле. Рассмотрим два тела: одно с массой   и другое с массой  . В эквивалентной проблеме одного тела рассматривают движение тела с приведённой массой, равной

где сила, действующая на эту массу, дается силой, действующей между этими двумя телами. Видно, что приведённая масса равна половине среднего гармонического двух масс.

Приведённая масса всегда меньше каждой из масс   или   или равна одной из них, если эта масса равна нулю. Пусть масса   значительно меньше массы   ( ), тогда приближённое выражение для приведенной массы будет

Движение тела с приведенной массой

Используя второй закон Ньютона, можно найти, что воздействие тела 2 на тело 1 задаётся силой

Тело 1 оказывает влияние на тело 2 посредством силы
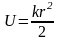