Вопрос 34.
1.Адиабатически изолированная термодинамическая система - система, в которой изменения её состояния могут происходить только благодаря механическим перемещениям частей системы и её оболочки (окружающих тел) и не могут происходить путём теплообмена с окружающими телами. Любое изменение состояния адиабатически изолированной системы называют адиабатическим процессом, а оболочку, окружающую такую систему - адиабатической оболочкой.
Так как при адиабатических процессах δQ = 0, то первое начало термодинамики для них можно записать в форме:
δA = - dU, (1)
Совместное применение этого выражения и уравнения Клапейрона-Менделеева позволяет получить уравнение, описывающее адиабатический процесс в идеальном газе. Для этого представим выражение (1) в виде
PdV = -MCvdT/μ, (2)
Нахождение полных дифференциалов от правой и левой частей уравнения Клапейрона-Менделеева дает:
PdV + VdP = MRdT/μ. (3)
Вычитание из этой формулы выражения (2) приводит его к виду
VdP = MRdT/μ + MCvdT/μ. (4)
С учетом соотношения Майера имеем:
VdP = MCpdT/μ. (5)
Умножим выражение (2) на отношение теплоемкостей γ = Cp/Cv и сложим его с формулой (5). Тогда получим
γPdV + VdP = 0. (6)
Величина γ называется показателем адиабаты. Формулы для теплоемкостей позволяют определить показатель адиабаты через количество степеней свободы i:
γ = (i+2)/i. (7)
Поделив уравнение (6) на произведение PV преобразуем его к виду
γd(lnV) + d(lnP) = 0. (8)
Откуда
PVɣ = const. (9)
Выражение (9) называется уравнением Пуассона в честь французского механика, математика и физика Симеона Дени Пуассона (1781 - 1840). Это уравнение адиабатического процесса для идеального газа, или адиабаты - кривой, описываемой этим уравнением в переменных P и V.
2.Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).
Существуют несколько эквивалентных формулировок второго начала термодинамики:
3.Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).
4.Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).
5.В современной термодинамике второе начало термодинамики изолированных систем формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (S).
Физический смысл энтропии состоит в том, что в случае, когда материальная система находится в полном термодинамическом равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии и совершают различные случайные хаотические движения.
общее число этих состояний, и есть энтропия.
Энтропия - физическая величина, количественно характеризующая особенности молекулярного строения системы, от которых зависят энергетические преобразования в ней.
3.Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных.
Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать на основе первого и второго начал термодинамики.
=>
=>
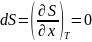