
- •Тема: «Расчет экстрактора»
- •Содержание
- •Введение
- •Государственный аграрный университет Северного Зауралья
- •Механико-технологический институт
- •Специальность 110303 – механизация переработки сельскохозяйственной продукции
- •Задание на курсовой проект
- •1. Расчет гладких обечаек нагруженных внутренним избыточным давлением
- •Расчет цилиндрических обечаек
- •1.2 Расчет конических обечаек
- •Расчет выпуклой крышки
- •2. Расчет обечаек, днищ и крышек, нагруженных наружным давлением
- •2.1 Расчет цилиндрической обечайки, нагруженной наружным давлением
- •2.2 Гладкие конические обечайки, нагруженные наружным давлением
- •3. Расчет сопряжений рубашки с корпусом
- •3.1 Сопряжение рубашки с корпусом сосуда при помощи кольца
- •3.2 Нагрузка от собственного веса.
- •4. Расчёт фланцевого соединения
- •4.9 Высота ( толщина ) фланца ориентировочно, м:
- •5. Расчёт на герметичность фланцевого соединения:
- •6. Подбор и расчёт опор
- •7. Укрепление вырезов отверстий
- •7.1 Отверстие под патрубок верхнего люка
- •Отверстие под патрубок дна сосуда
- •Отверстие под входной патрубок рубашки сосуда
- •Отверстие под выходящий патрубок рубашки сосуда
- •Заключение
- •Список литературы
4. Расчёт фланцевого соединения
4.1 Определение конструктивных параметров соединения
1. Толщина S0 втулки фланца в зависимости от его конструкции (тип фланца – свободный) принимается таким образом, что удовлетворяет условию S0 > S.
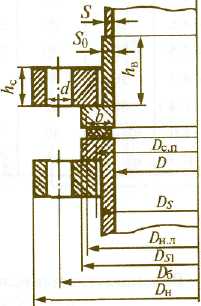
Рисунок 4 – Расчётная схема
4.2 Высота hв втулки свободного фланца:
|
|
4.3 Внутренний диаметр свободного кольца Ds принимаем .
|
|
4.4 Диаметр Dб болтовой окружности фланцев:
|
|
где u1 – нормативный зазор между гайкой и обечайкой (u1 = 8 мм);
d6 =20 мм – наружный диаметр болта
Ds – внутренний диаметр свободного кольца.
4.5 Наружный диаметр фланца:
|
|
где а – конструктивная добавка для размещения гаек по диаметру фланца
4.6 Наружный диаметр прокладки выбираем с учетом условия
|
|
где Ds1
– наружный
диаметр бурта (![]() ).
).
4.7 Средний диаметр прокладки
|
|
где b – ширина прокладки
4.8 Определяем количество болтов, необходимое для обеспечения герметичности соединения:
|
|
где tш – рекомендуемый шаг расположения болтов, выбираемый в зависимости от давления (при Pр = 0,6 –1,0 МПа tш = (4,0 · 20) dб).
Полученное значение округляем до значения, кратного четырём.
4.9 Высота ( толщина ) фланца ориентировочно, м:
|
|
где λф = 0,3.
 Sэкв
– эквивалентная
толщина втулки фланца, м.
Sэкв
– эквивалентная
толщина втулки фланца, м.
|
|
5. Расчёт на герметичность фланцевого соединения:
5.1 Определяем нагрузки в соединений при монтаже – Fб1 и в рабочих условиях - Fб2 (см. рис. 5)
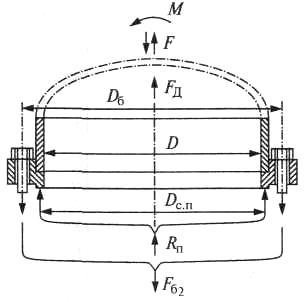
Рисунок 5 – Схема действия нагрузок на фланец в рабочих условиях
5.2 Равнодействующая от сил внутреннего давления в МН
|
|
5.3 Реакция прокладки:
|
|
где b0 – эффективная ширина прокладки, м ( при b < 15 мм b0 = b = 15 мм );
kпр – коэффициент, зависящий от материала и конструкции прокладки
|
|
5.4 Определяем усилие, возникающее от температурных деформаций
где αф, αб, αс – соответственно коэффициенты линейного расширения материала фланца, болтов и свободного кольца);
tф, tб, tс - соответственно температуры фланца, болтов, свободного кольца (табл.7);
yб, yп, yф, yс – податливости соответственно болтов, прокладки, фланцев, свободного кольца, определяемые по формулам:
|
|
где Eб – модуль упругости материала болтов (табл. 8)
fб – расчётная площадь поперечного сечения болта по внутреннему диаметру резьбы
lб – расчётная длина болта, м.
|
|
где lбо – расстояние между опорными поверхностями головки болта и гайки, определяется по формуле
|
|
где hп – высота стандартной прокладки;
d = dб – диаметр отверстия под болт, м.
Податливость прокладки
|
|
где кп = 0,09 – коэффициент обжатия прокладки из резины;
Еп – модуль упругости материала прокладки (табл. 5).
 Податливость
фланцев
Податливость
фланцев
|
|
где Е – модуль упругости материала фланца, Н/м2;
v, λф – безразмерные параметры.
|
|
|
|
где ψ1 ψ2 – коэффициенты, определяемые по формулам:
|
|
|
|
|
|
где Ес – модуль упругости материала фланца, Н/м2;
hс – высота свободного кольца, м (hс= hф ).
5.5 Коэффициент жесткости фланцевого соединения при стыковке фланцев одинаковой конструкции:
|
|
 5.6
Болтовая нагрузка в условиях монтажа
до подачи внутреннего давления:
5.6
Болтовая нагрузка в условиях монтажа
до подачи внутреннего давления:
|
|
где: F – внешняя осевая растягивающая ( + ) или сжимающая ( - ) сила ( F = 0 – в нашем случае);
М – внешний изгибающийся момент ( М = 0 );
[σ]σ20 – допускаемое напряжение для материала болта при 20º С, Н/м2
Рпр – минимальное давление обжатия прокладки, МПа.
5.7 Болтовая нагрузка в рабочих условиях:
|
|
5.8 Приведённый изгибающий момент:
|
|
5.9 Проверяем условия прочности болтов
|
|
|
|
где [σ]б = 168 МПа– допускаемое напряжение для материала болта при расчётной температуре
 5.10
Проверяем условие прочности
неметаллических прокладок:
5.10
Проверяем условие прочности
неметаллических прокладок:
|
|
где
![]() ,
,
[ Рпр ] – допускаемое давление на прокладку 18 МПа
5.11 Максимальное напряжение в сечении, ограниченном размером S0:
|
|
|
|
где σ1 – максимальное напряжение в сечение фланца, ограниченном размером Sх ,МПа,
fф – безразмерный параметр, определяемый по монограмме в зависимости от S1/S0
Тф - безразмерный параметр, находим по формуле:
|
|
5.12 Напряжение во втулке от внутреннего давления:
Тангенциальное
|
|
меридиональное
|
|
 5.13
Проверяем усилие прочности для сечения
фланца, ограниченного размером S0:
5.13
Проверяем усилие прочности для сечения
фланца, ограниченного размером S0:
|
|
где [σ]б
– допускаемое напряжение для фланца в
сечении, принимаемое при количестве
нагружении соединений 2·103
![]()
5.14 Проверяем условие прочности для свободного кольца:
|
|
где М0с – приведённый изгибающийся момент, определяемый из условия.
|
|
5.15 Допускаемое напряжения для материала свободного кольца при 20º С и расчётной температуре соответственно
[σ]с20 = σт.с.20 , |
|
[σ]с = σт.с, |
|
где σт.с.20 и σт.с.– предел текучести материала кольца соответственно при 20º С и расчётной температуре.
5.16 Проверяем условие герметичности, определяемое углом поворота свободного кольца:
|
|
где [ Q ]c = 0,026 рад – допустимый угол поворота кольца.

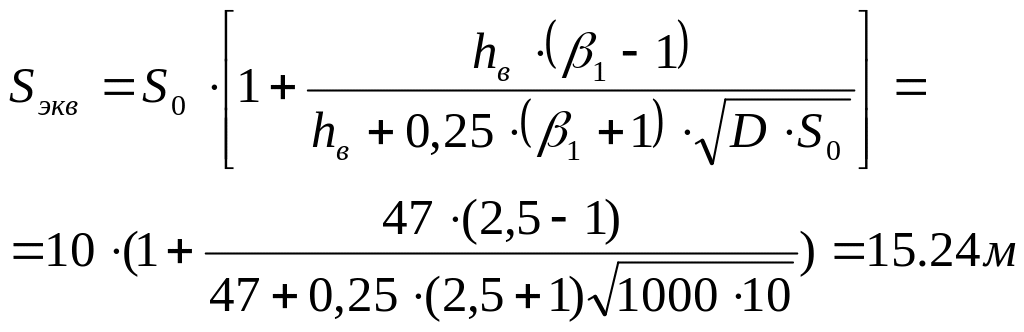
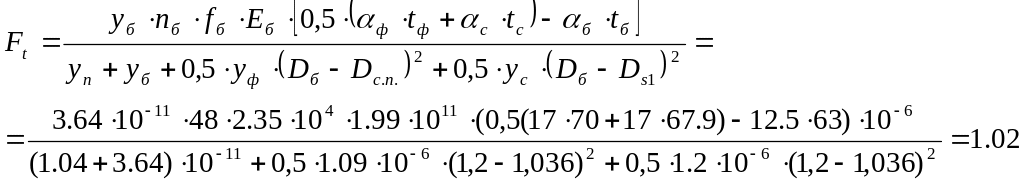
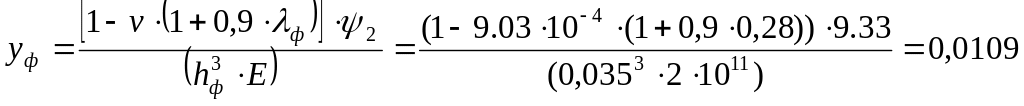 ,
,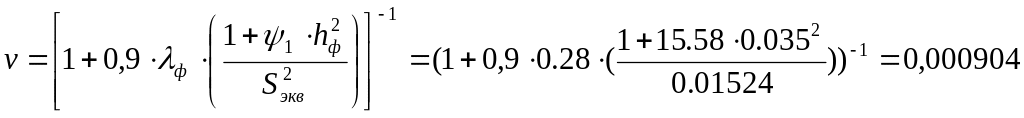 ,
,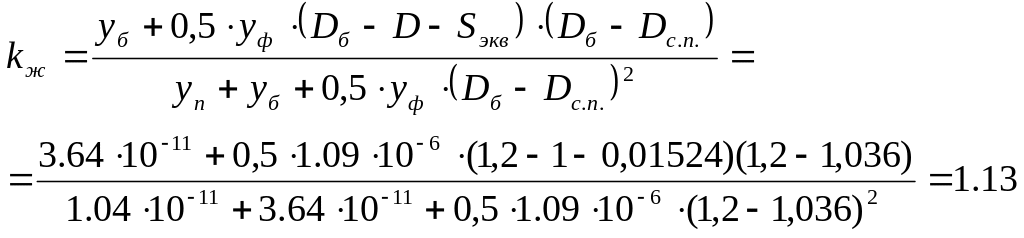 .
.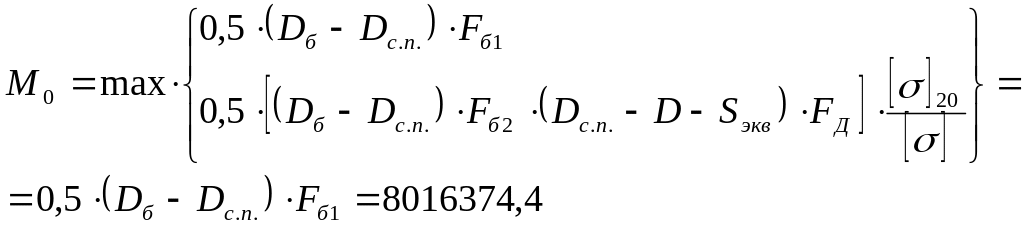
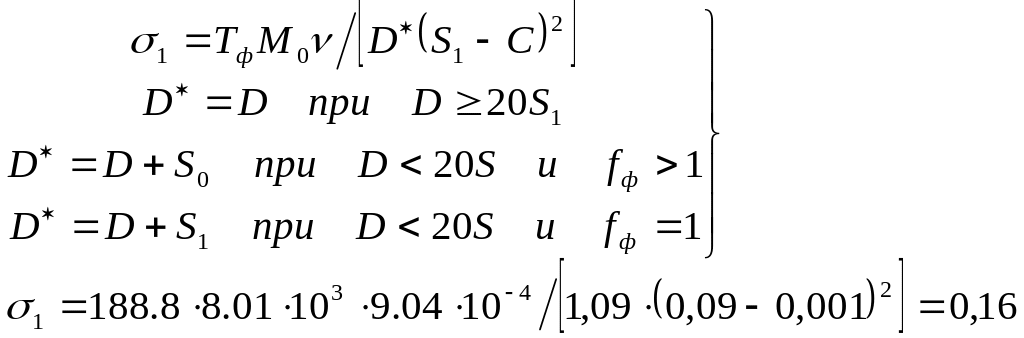 ,
,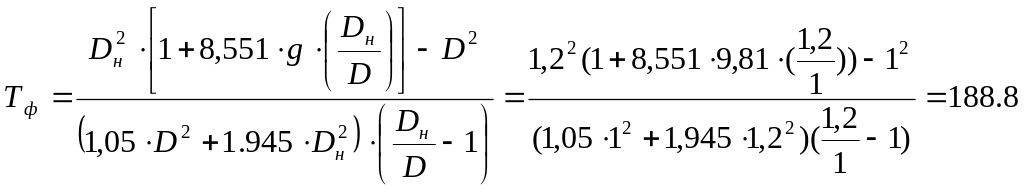 .
.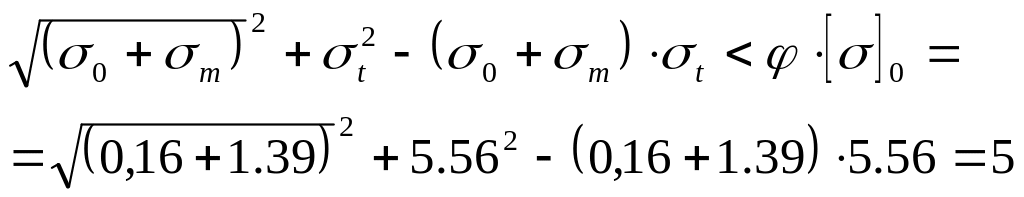
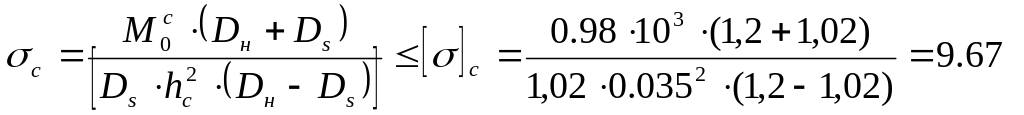 МПа,
МПа,