Дисперсия абсолютно непрерывной случайной величины

Дисперсия абсолютно непрерывной с.в. X определяется формулой:

.

Если интеграл справа сходится, то говорят, что дисперсия существует и конечна. Если же он расходится (то есть равен ), то говорят, что дисперсия не существует.

Все свойства дисперсии 1–4, в случае конечного вероятностного пространства, остаются справедливыми и для абсолютно непрерывных с.в.

Вычислим дисперсию с.в. X, равномерно распределенной на отрезке :

.

Вычислим дисперсию с.в. X, имеющей показательное распределение с параметром :

.

Вычислим дисперсию с.в. X, имеющей нормальное распределение с параметрами a и :

.

Математическая статистика Обработка результатов измерения

Предположим, что задано некоторое вероятностное пространство (,F, P). В дальнейшем оно нас не будет интересовать. Рассмотрим случайный эксперимент, который мы умеем воспроизводить в одних и тех же условиях некоторое (а лучше –неограниченное) число раз. Его свойства частично или полностью неизвестны. Пусть X:R — с.в., наблюдаемая в случайном эксперименте. Например, контролируем размеры производимой на заводе детали или делаем опрос общественного мнения. Об объекте исследования можно мыслить как о некоторой с.в. X. Проведя n раз эксперимент в одинаковых условиях, получим числа — значения наблюдаемой с.в. в первом, втором и т. д. экспериментах, называемые выборкой. Выборки производятся для того, чтобы понять свойства объекта исследования. Рассмотрим подробнее это понятие.

В серии уже произведённых экспериментов выборка — это набор чисел. До того как эксперимент проведён, имеет смысл считать выборку набором случайных величин (независимых и распределённых так же, как X). Действительно, до проведения опытов мы не можем сказать, какие значения примут элементы выборки: это будут какие-то из значений с.в. X. Поэтому имеет смысл считать, что до опыта X_k — с.в., одинаково распределённая с X, а после опыта — число x_k, которое мы наблюдаем в k-м по счёту эксперименте, т.е. одно из возможных значений с.в. X_k. В результате экспериментов мы получаем случайные величины, имеющие ту же функцию распределения, что и измеряемая величина X. Дадим более строгие определения, принятые в математической статистике.

Определение 1. Генеральной совокупностью называется совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом.

Определение 2. Выборкой объема n, измеряющего с.в. , называется набор случайных величин , удовлетворяющих следующим условиям:

1) с.в. независимы в совокупности;

2) , , .

Это равенство означает совпадение функций распределения с.в. X_k и X.

Определение 3. Реализацией выборки называют конкретные значения выборки, полученные в результате наблюдений (испытаний).

При составлении выборки после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен в генеральную совокупность или не возвращен. В связи с этим различают повторные и бесповторные выборки.

Определение 4. Повторной называется выборка, при которой отобранный объект возвращается в генеральную совокупность перед извлечением следующего объекта.

Определение 5. Бесповторной называется выборка, при которой отобранный объект не возвращается в генеральную совокупность.

Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной, то есть наиболее полно представляла изучаемые признаки генеральной совокупности. Согласно закону больших чисел условием обеспечения репрезентативности выборки является соблюдение случайности отбора, то есть все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку.
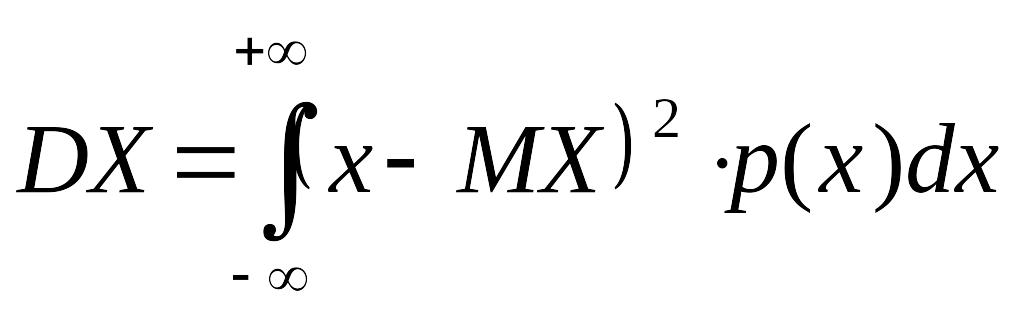