Интервальные оценки параметров распределения

Точечные оценки неизвестного параметра  хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток состоит в том, что неизвестна точность оценивания параметра. Поэтому и возникает задача о приближении параметра  не одним числом, а целым интервалом. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки некоторого параметра  справедливо неравенство , то число характеризует точность оценки. Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 20. Надёжностью (доверительной вероятностью) оценки параметра  называется вероятность  того, что выполняется неравенство .

Если заменить это неравенство двойным неравенством , то получим, что надёжность определяется как

.

Определение 21. Доверительным называется интервал, в который попадает неизвестный параметр с заданной надёжностью .

Иными словами, доверительный интервал покрывает неизвестный параметр  с заданной надёжностью . Выбор величины доверительной вероятности зависит от постановки задачи. Чаще всего берутся значения  =0,9; 0,95; 0,99; 0,997.

Построение доверительных интервалов (д.И.) нормального распределения

Пусть исследуемая с.в. XN(a, ). Значения вариант выборки - независимые с.в., каждая из которых также принадлежит N(a, ). Построим д.и. для параметров этого распределения.

1) Д.И. Для математического ожидания при известной дисперсии

Рассматривается случай, когда дисперсия DX= известна, а в роли неизвестного параметра  выступает значение MX=a. Зададимся надежностью и найдём д.и. для математического ожидания.

Интервальная оценка для математического ожидания имеет вид:

.

Значение определяется из таблиц для функции Лапласа так, чтобы .

2) Д.И. Для математического ожидания при неизвестной дисперсии

Пусть теперь параметр  нормального закона распределения признака Х генеральной совокупности неизвестен. Вычислим по оценку = параметра  =а и исправленную дисперсию 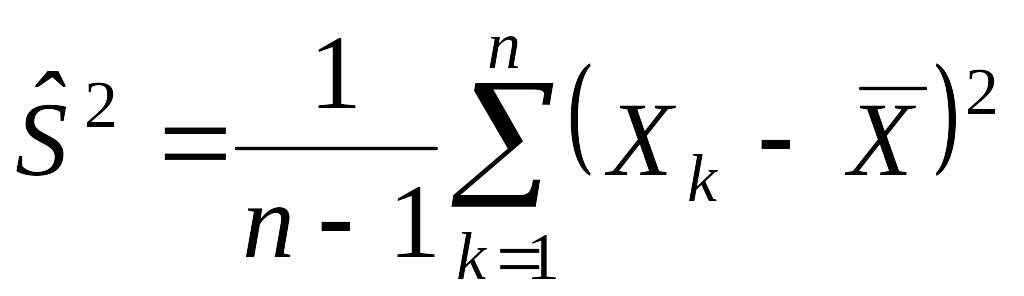, которая является точечной оценкой для дисперсии . С вероятностью можно заключить, что выборочное среднее дает значение неизвестного математического ожидания с точностью , а доверительный интервал определяется как, 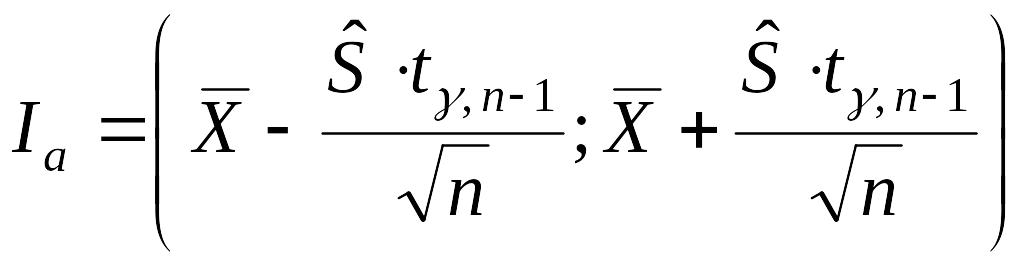, где величина распределена по закону Стьюдента с (n-1) степенями свободы (ее значения находятся по таблице).

3) Д.И. Для неизвестной дисперсии

Пусть с.в. XN(a,²), причем неизвестным параметром  является σ. Вычислим по выборочное среднее и точечную оценку дисперсии . В качестве оценки неизвестного среднего квадратического отклонения возьмем . С вероятностью можно утверждать, что интервал

накроет неизвестное среднее квадратическое отклонение .

С такой же вероятностью можно утверждать, что интервал

накроет неизвестную дисперсию . Для заданных и число, находят по таблицам - распределения.

Замечание. Если q_ > 1, то с учетом условия σ > 0 д.и. для σ будет иметь границы , то есть .
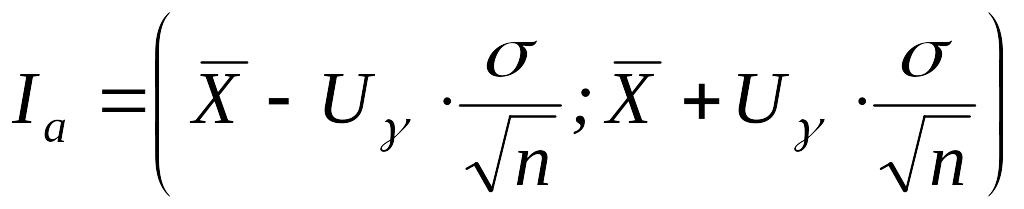