Связь линейных и угловых величин:

                               

2. Динамика материальной точки. Первый закон Ньютона. Масса. Сила. Инерциальные системы отсчета.

Тела, окружающие материальную точку (тело), способны оказать на неё определенное влияние, действие.

Влияние тел (или частиц) на движение друг друга называют взаимодействием.

Взаимодействие тел является причиной их ускорений, а ускорение - следствием их взаимодействия. Так, например, с ускорением движутся падающие на Землю тела. Действие тел друг на друга является причиной изменения формы и объёма тел (причиной деформации тел).

Взаимодействие тел характеризуется некоторой величиной, являющейся функцией положений (г) и скоростей (v) взаимодействующих тел. Мера механического воздействия на тело со стороны других тел, в результате, которого данное тело получает ускорение или деформируется, называется силой F. Под действием силы тело

- либо изменяют вектор скорости, т.е. приобретают ускорение (динамическое проявление F),

- либо изменяют свою форму и размеры, т.е. деформируются (статическое проявление F).

Сила - это векторная величина, которая характеризуется числовым значением, направлением в пространстве и точкой приложения.

ПЕРВЫЙ ЗАКОН НЬЮТОНА

Если на тело не действуют силы, то механическое состояние тела не изменяется: тело не движется (не изменяются координаты тела, тело находится в состоянии покоя) или движется с постоянной скоростью (не изменяется скорость, тело движется без ускорения).

Свободной материальной точкой называют материальную точку, которая не взаимодействует с другими телами. Если действие сил скомпенсировано, то точка - квазисвободная.

Движение свободной или квазисвободной частицы называется движением по инерции.

Закон инерции: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.

Характер движения зависит от выбора системы отсчета. Одно и то же движение в разных системах отсчета выглядит по-разному.

Существуют такие системы отсчета, в которых свободная материальная точка движется равномерно и прямолинейно из любого начального положения в любом направлении. Такие системы отсчета называются инерциальными системами отсчета (ИСО). Системы отсчета, в которых нарушается закон инерции называются неинерциальными.

Если частица свободная, то она движется с постоянной скоростью или покоится относительно инерциальной системы отсчета. Кинематическое уравнение движения для свободной материальной точки можно записать - радиус-вектор материальной точки.

Способность тел сохранять состояние покоя или равномерного прямолинейного называется инертностью. Мерой инертности тела является физическая величина, называемая массой тела.

Масса (тела) — физическая величина, являющаяся одной из характеристик материи, определяющая её инерциальные (инертная масса). Свойства инертной массы.

1. Величина инертной массы не зависит от величины и направления действия сил.

2. Масса аддитивна - масса системы тел равна сумме масс тел, входящих в систему.

Величины инертной массы не зависит от величины и направления сил.

Масса аддитивна – масса системы тел равно сумме масс тел, входящих в систему.

Первый закон Ньютона - это закон инерции. Инерция - стремление тела сохранить состояние покоя или равномерного (прямолинейного) движения.

Первый закон Ньютона формулируется следующим образом: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной системой отсчета. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Инерциальных систем существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

Первый закон Ньютона отражает то, что в инерциальных системах отсчета:

• пространство однородно и изотропно,

• время однородно.

Однородность пространства означает, что все точки пространства эквивалентны.

Изотропность пространства означает, что все направления эквивалентны (равноправны).

Однородность времени означает, что все моменты времени эквивалентны.

5. Второй закон Ньютона как уравнение движения. Третий закон Ньютона. Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). Формулировка: В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. При подходящем выборе единиц измерения, этот закон можно записать в виде формулы :a⃗ =F⃗ /m ,где a⃗ — ускорение материальной точки;F⃗ — сила, приложенная к материальной точке;m — масса материальной точки.Или в более известном виде: F⃗ =ma⃗ .

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс: В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. dp⃗ /dt=F⃗ , где p⃗ — импульс точки, p⃗ =mv⃗ , где v⃗ — скорость точки; t — время; dp⃗ /dt — производная импульса по времени. Третий закон Ньютона. Формулировка: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно.

6 . Закон всемирного тяготения. Закон тяготения, открытый в 17 в. И. Ньютоном, формулируется следующим образом. Каждые две материальные частицы притягивают друг друга с силой F, прямо пропорциональной их массам m1 и m2 и обратно пропорциональной квадрату расстояния r между ними:

(1)

с ила F направлена вдоль прямой, соединяющей эти частицы. Коэффициент пропорциональности G —гравитационная постоянная, равная6,67*10^-11 м³/(кг с²). Под "частицами" здесь подразумеваются тела, размеры которых пренебрежимо малы по сравнению с расстояниями между ними, т. е. материальные точки. Н. з. т. можно интерпретировать иначе, полагая, что каждая материальная точка с массой m1 создаёт вокруг себя поле тяготения (гравитационное поле), в котором любая другая свободная материальная точка, находящаяся на расстоянии r от центра поля, приобретает ускорение, не зависящее от своей массы, равное

(2) и направленное к центру поля. 7. Импульс. Закон сохранения импульса. Центр масс. Закон движения центра масс. Импульс тела - это физическая векторная величина, равная произведению массы тела на его скорость. Импульс это векторная величина, при этом его направление всегда совпадает с направлением скорости. Единицей импульса является килограмм на метр в секунду (1 кг*м/с). p=m*v Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. или

Центр масс-геометрическая точка, характеризующая движение тела или системы частиц как целого. Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом: где   — радиус-вектор центра масс,   — радиус-вектор i-й точки системы,   — масса i-й точки. Теорема о движении центра масс системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему. Формулировка: Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил. Формула (6) является математическим выражением теоремы о движении центра масс системы. или

8. Энергия, работа, мощность. Работа переменной силы. Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Работа силы- мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения. Если сила F численно и по направлению постоянна, а перемещение М0М1 прямолинейно (рис. 1), то работа A = F•s•cosa, где s=M0M1, a — угол между направлениями силы и перемещения. Когда a<90°, Р. силы положительна, при 180°>a>90° — отрицательна, а при a=90°, т. е. когда сила перпендикулярна перемещению А=0. Единицы измерения : джоуль (в СИ), 1 эрг=10-7 Дж и килограмм-сила на метр (1 кгс•м=9,81 Дж). Мощность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Различают среднюю мощность за промежуток времени и мгновенную мощность в данный момент времени: Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время: Работа переменной силы. В случае движения под действием переменной силы величина работы рассчитывается следующим образом. 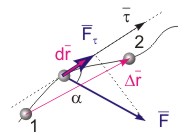Всю траекторию мысленно разбивают на отдельные участки такой малой длины |dr|, что действующую на них силу можно считать постоянной (см. рис. 7.2). Проекция силы на направление вектора элементарного перемещения dr представляет собой ее тангенциальную составляющую. Следовательно, элементарную работу на перемещении dr можно рассчитать с помощью соотношения (7.2) dA = (F, dr) = Fdr·dr = Fτ·dr. (7.2) Работа на конечном перемещении рассчитывается путем интегрирования согласно выражению (7.3): (7.3)