25. Второе начало термодинамики. Энтропия. Статистический смысл энтропии.

Второе начало термодинамики может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики может быть также сформулировано следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращения этого тепла полностью в работу.

Энтропи́я — в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния.

 Степень упорядоченности системы характеризуется ее энтропией. Поэтому между энтропией состояния и его веро­ятностью должна существовать определенная зависимость, ко­торую Л. Больцман выразил такой формулой  s=kLnp_тд, где к — постоянная Больцмана: (k=(R/N_A)= 1,37 10^-23 Дж К^-1 )p_тд — термодинамическая вероятность (число возможных микро­состояний, которыми может быть реализовано данное макросо­стояние системы). Таким образом, естественный ход энергетических превраще­ний в изолированной системе переводит ее из состояния с меньшей энтропией в состояние с большей энтропией. Такое из­менение энтропии отображает диссипацию энергии. Это поло­жение более строго сформулировано во втором начале термоди­намики.

26. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: где p — давление; V — объем T — температура; Z_r = Z_r (p,T)  — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная.

Уравнение Ван-дер-Ваальса - термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид: где  — давление,

 — молярный объём,  — абсолютная температура,  — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка   учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка   — объем молекул газа.

Для   молей газа Ван-дер-Ваальса уравнение состояния выглядит так: где  — объём,

Ван-дер-ваальсовы силы — силы межмолекулярного (и межатомного) взаимодействия с энергией 10 — 20 кДж/моль.

Ван-дер-Ваальсовы силы межатомного взаимодействия инертных газов обусловливают возможность существования агрегатных состояний инертных газов (газ, жидкость и твёрдые тела).

К ван-дер-ваальсовым силам относятся взаимодействия между диполями (постоянными и индуцированными). Название связано с тем фактом, что эти силы являются причиной поправки на внутреннее давление в уравнении состояния реального газа Ван-дер-Ваальса. Эти взаимодействия в основном определяют силы, ответственные за формирование пространственной структуры биологических макромолекул.

Ван-дер-ваальсовы силы также возникают между частицей (макроскопической частицей или наночастицей) и молекулой и между двумя частицами.

Изотермы Ван–дер–ВаальсаУравнение Ван–дер–Ваальса (6.4.3) после несложных преобразований можно представить в виде уравнения третьей степени относительно объёма: .     (6.4.4)Это уравнение имеет три корня, т.е. при данных значениях температуры и давления могут быть три значения молярного объёма или три значения плотности газа. Корни могут либо все три вещественные, либо два из них мнимые и один – вещественный. Физический смысл имеют лишь вещественные положительные корни, поэтому мнимые корни не будем рассматривать. Чтобы выяснить значение корней уравнения Ван-дер-Ваальса, рассмотрим изотермы уравнения (6.4.3) (рисунок 6.4.1) и сравним их с экспериментальными изотермами (рисунок 6.4.2). 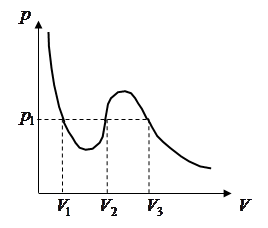Рисунок 6.4.1 – Изотермы Ван-дер-Ваальса (решение уравнения 6.4.4)