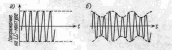2.2 Исследуемые закономерности.

Между зеемановскими под уровнями возможны самопроизвольные (спонтанные) и вынужденные (индуцированные) квантовые переходы с правилом отбора 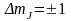. Самопроизвольные переходы происходят только в одном направлении—с более высоких уровней на низшие. Вынужденные переходы возможны только под действием внешнего источника энергии, например, внешнего электромагнитного поля. Энергия квантов поля должна совпа­дать с энергетическим зазором между соседними зеемановскими подуровнями:

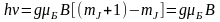(2.1)

Вынужденные переходы в отличие от спонтанных равновероятны в обоих направлениях, 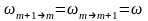. Вероятность 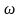таких переходов пропор­циональна плотности энергии электромагнитного поля. При переходе на более высокий уровень атом поглощает из поля квант энергии 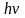, Наоборот, при переходе с высокого уровня на низший атом излучает фотон с энергией .

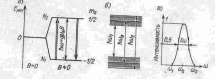
Рис 3 Зеемановские дублет уедниенного атома с J=1/2 (а), энергетические зоны в реальных образцах (б) и форма линии резонанцного индуцированого поглашения энергии (в)

На рис. 3, а, изображен зееманевский энергетический дублет (два уровня) атома с 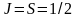(например, уровни в магнитном поле В валентного электрона натрия*). Вынужденные переходы с поглощением и излучением фотона показа­ны соответственно стрелками вверх и вниз.

В большом ансамбле атомов число их на нижнем уровне 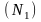и верхнем 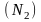неодинаково, обычно 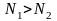. Вследствие этого число переходов с поглощением фотонов больше, нежели с излучением фотонов. Следовательно, при выполнении условия (2.1) за счет индуцированных переходов между зеемановскими подуровнями из электромагнитного поля поглощается энергия.

Эффекта резонансного поглощения ансамблем атомов энергии электромагнитного поля можно достигнуть двумя способами. Можно для заданного поля В подбирать частоту v квантов электромагнитного поля такой, чтобы обеспечивалось условие (2.1); частота резонансного поглощения составит тогда

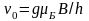(2.2)

Если частота 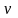фиксирована, можно изменением индукции , поля В менять энергетический зазор между зеемановскими уровнями. Резонансное значение индукции поля В составляет

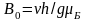(2.3)

В радиоспектроскопии используются оба метода для поиска и прохождения линий резонансного поглощения.

Пропорциональность между частотой и индукцией поля Вв со­отношениях (2.2), (2.3) используется в современной квантовой магнитометрии.

Мощность, поглощаемая ансамблем атомов при ЭПР, пропорциональна вероятности вынужденных переходов, разности заселенностей 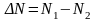соседних зеемановских уровней и энергии кванта _:

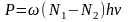
Отношение заселенностей уровней в состоянии термодинамического равновесия определяется коэффициентом Больцмана, 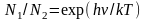_. При обычных условиях n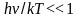 поэтому 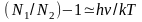. Принимая приближенно 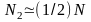(здесь 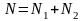— число атомов в системе), имеем 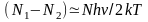, следовательно, поглощаемая при резонансе мощность

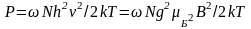(2.4)

Заметим, что мощность 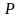пропорциональна квадрату частоты (или индукции 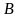), числу атомов 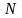, обратно пропорциональна температуре 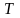. Это наиболее существенные факторы, от которых зависит интенсивность сигналов ЭПР.

Поглощение энергии при ЭПР не носит характера узкого, 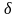-образного резонанса. Вследствие взаимодействия магнитных диполей близких атомов, неизбежной неоднородности внешнего поля В, других факторов каждый атом (или ассоциации атомов) находится во внутреннем, локальном поле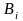 . Для реального образца зеемановские уровни у единенного атома, как на рис. 3, а, трансформируются в квази непрерывные энергетические зоны (рис. 3), и ансамбль атомов спосо­бен поглощать энергию в интервале частот .

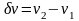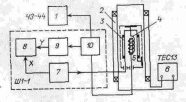
Рис 4. Лабораторная установка для исследования вынужденных электронных квантовых переходов между зеемановскими уровнями атомов в слабом магнитном поле

Резонансная линия имеет, следовательно, колоколообразный вид, как качественно показано на рис. 3, в, с шириной, оцениваемой интервалом частот . Сопоставляя интервалу частот 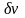неопределенность энергии атома 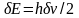, можно по соотношению Гейзенберга—Бора

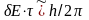(2.5)

оценить время жизни 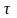атома в возбужденном (на верхнем зеемановском уровне) состоянии.

Экспериментальная установка и методика наблюдения вы­нужденного резонансного поглощения. Изучение вынужден­ных электронных переходов осуществляется здесь в слабом магнитном .поле с индукцией 10—30 Тл (1—3 мТл) на лабораторном макете спектрометра ЭПР (рис. 4). Магнитное поле В создается кольцами Гельмгольца 2 системой двух круговых катушек с током, среднее расстояние между которыми равно их среднему радиусу. Такая система создает в геометрическом центре поле с однородностью, достаточной для данного эксперимента. Индукция поля в центре колец Гельмгольца определяется формулой

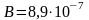
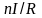(2.6)

Здесь 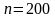- число витков на одной катушке, 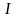- сила тока в 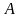, , 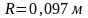средний радиус катушек; индукция дается в Тл. Кольца Гельмгольца питаются от стабилизированного регулируемого источника тока 6.

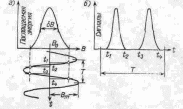
Рис 5. Динамический метод регистрации сигналов ЭПР

В работе применен динамический (в отличие от статического—снятия по точкам) метод наблюдения линии резонансного поглощения—многократное сканирование с частотой 50 Гц резонансного условия 1 (2.1), как показано на рис. 5, а. Для этого на резонансное поле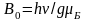 в накладывается с помощью дополнительных (модуляционных) катушек 3 модуляционное поле вида 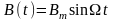причем амплитуда модуляц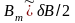ии . Из рис. 5, а видно тогда, что за период модуляции 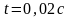с возникает дважды между временем

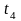и и резонансное поглощение, как пока­зано на рис. 5,б,

Электромагнитное поле частоты т создается катушкой индуктивности 4, в которой располагается исследуемый образец 5, Катушка 4 является элементом LC-контура генератора слабых колебаний 10 (автодина). В обычных условиях (вне резонанса) амплитуда колебаний автодина неизменна (рис. 6, а). При вхождении в резонанс часть энергии электромагнитного поля катушки поглощается образцом, при этом уменьшается добротность LC-контура, следовательно, уменьшается амплитуда колебаний автодина. При периодическом прохождении резонанса, как на рис. 5, напряжение на LC-контуре автодина становится модулированным (рис, 6,б). Это напряжение детектируется, усиливается (блок 9) и подается на У—вход осциллографа 8; развертка осциллографа синхронизирована с током модуляционного генератора 7. Частота автодина контролируется частотомером .

Автодин, детектор и усилитель, осциллограф и модуляционный генератор являются здесь элементами заводского прибора Ш1-1. Модуляционные катушки 3, катушка 4 с об­разцом 5 оформлены конструктивно в виде отдельного узла, экранированного от внешних помех латунным по серебренным кожухом, жестко закрепленным на основании колец Гельмгольца.

Рис 6. Напряжение на LC – контуре автодина: a – вне ЭПР , б – при периодическом прохождении ЭПР