1.4 Определители третьего порядка

Определителем матрпцв! A размера 3x3 называют число, вычисляемое по пра­вилу, изображенному на рис 2. Обозначение преяснее.

Рис. 2: Правило треугольника вычисления определителя 3-го порядка.

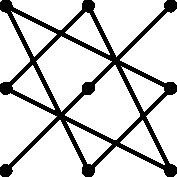
Можно указать и аналитическую формулу:

a 11 a 12 a 13 ∆ = detA= \A\ = a21 a22 a23 =

a31 a 32 a 33 = a11a22a33 + a 12a23a31 + a13a21a32 - (a13a22a31 + a12a21a33 + a 11a23a32).

Пример 8,

\A\ =

1	-2	3
1	0	6
4	-5	2

= 1 • 0 • 2 + (-2) • 6 • 4 + 3 • (-1) • (-5)-(3-0-4 + 1-6-(-5) + (-2)-(-1)-2) = = 0 - 48 + 15 - 0 + 30 - 4 = -7.

Задача 1. Вычислите определители матриц

A=

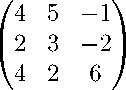
2	-3	1
4	-2	0
2	1	-

B=

Ответ: \A\ = 0, \B\ = -4.

August 31, 2013 Курбатов В.Г. 8

1.5 Свойства определителей

в этом параграфе обсуясдаются свойства определителей третьего порядка. По­лезно уясе сейчас иметь в виду, что точно такие ясе свойства имеют место и для определителей любого порядка.

Свойство 1. При транспонировании матрицы ее определитель не меняется: \A'\ = \A\.

Свойство 2. Если поменять местами две строки {или два столбца), то определитель изменит знак на нротивонолож.ный, но но абсолютной величине не изменится.

Свойство 3. Определитель, имеющей две одинаковые строки (или два одинаковых столбца), равен нулю.

Свойство 4. Если строку (столбец) определителя умнож.ить на некоторое число, то определитель умиоукится на это число. Общий множ.итель из строки (столбца) МОЖ.НО выносить за знак определителя.

Свойство 5. Определитель, имеющий две пропорциопальпые строки (или столбца) равен нулю.

Свойство 6. Если определитель имеет нулевую строку (или столбец), то он равен нулю.

Свойство 7. Если определители ∆1 я ∆2 отличаются только k-ми строками (столб­цами), то их сумма ∆1 + ∆2 равна определителю ∆, k-ая строка (столбец) которого является суммой k-х строк (столбцов) определителей ∆1 и ∆2, а остальные строки (столбцы) — такие ж:е как в определителях ∆1 и ∆2. Например, если k = 2, то

a11	a12 + a12	a13		a11	a12	a13		a11	a 12	a13
a21	a22 + a22	a23	=	a21	a22	a23	+	a21	a 22	a23
a31	a 32 + a32	a33		a31	a32	a33		a31	a 2	a33

Свойство 8. Определитель не изменится, если к какой-либо его строке (столбцу) прибавить другую строку (столбец), умнож:енную на число.

Обоснование:

a11 a12 + a11 a13

a21 a22 + a21 a23 a31 a32 + a31 a33

a11 a12 a13 a21 a22 a23 a31 a32 a33

a11 a11 a13 a21 a21 a23 a31 a31 a33

Свойство 9. Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.

Например,

5 0

7

= 3 • 5 • 7.

Свойство 10. Определитель произведения двух матриц A и B равен произведению

определителей этих матриц: \AB\ = \A\ ■ \B\.

August 31, 2013 Курбатов В.Г. 9