7.9 Гипербола

Гиперболой называют кривую, заданную уравнением

x

y² b²

1.

August 31, 2013 Курбатов В.Г.

57

Само уравнение называют каноническим уравнением гиперболы. Числа a и b на­зывают полуосями, а точки пересечения с осями — вершинами. Прямые y = ±-x называют асимптотами гиперболы. Если a = b гиперболу называют равносторон­ней. Точки с координатами (c, 0) и (—c, 0), где c = ya? + b, называют фокусами.

-a

X

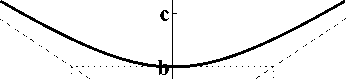
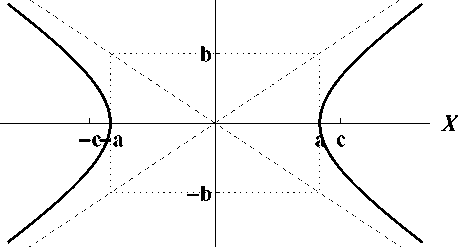
Рис. 8: Гиперболы с уравнениями ^

21

62

= 1 И

62

= 1

Правило рисования: Сначала рисуют прямоугольник с полуосями a и b, затем через его вершины проводят асимптоты, а затем — саму гиперболу.

Рис. 9: Гиперболы y = - -а y = —-

Кривая y = - является равносторонней гиперболой, повернутой но отношению к канонической на угол 45°.

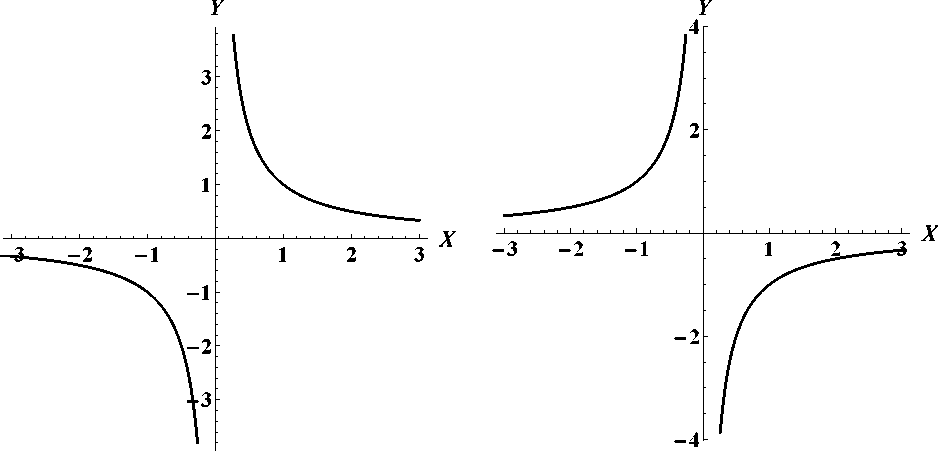
August 31, 2013 Курбатов В.Г.

58

7.10 Парабола

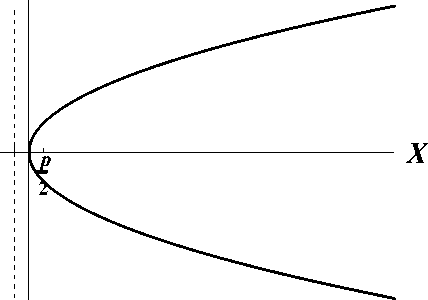
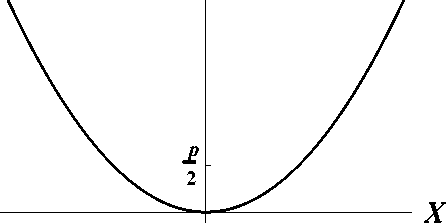
Параболой называют кривую, заданную уравнением

y² = 2px.

Само уравнение называют каноническим уравнением параболы. Число p называют параметром параболы, а точку (0,0) — вершиной. Точку с координатами (^p ₂,0) на­зывают фокусом, а прямую x = - ^p ₂ — директрисой.

Рис. 10: Параболы y2 = 2px и 2 py = x2

Задача 36. Построить кривую y = -2x2 + 6x + 3. Решение. Выделим полный квадрат:

y = -2x2 + 6x + 3,

	y = -2(x2 - 3x) + 3,
y=	/ 2 3 32 32
y=	x 2 3 32\ 9
	2/ 3\ 15
	15 / 3\ y-2 = -2 x-2).

Птак, получилась парабола y

2x ², верп1ина которой смещена в точку |, ₂

7.11 Уравнение плоскости

Общим уравнением плоскости называют уравнение вида

Ax+By +Cz +D = 0

August 31, 2013 Курбатов В.Г.

59

Рис. 11: Парабола из задачи 36

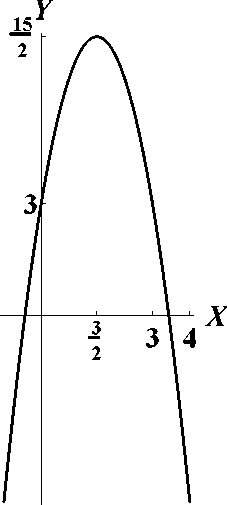
в предполоясении, что хотя бы один из коэффитщеитов A, B или C отличен от нуля. Покажем, что вектор n ¯ = (A, B, C) является перпендикулярным плоскости. Вектор n ¯ = (A, B, C) называют нормальным от слова "нормаль" вектором плоскости. Пусть точка Mo(xo,yo,zo) принадлежит плоскости, т. е.

Axо + Byо + Czo + D = 0.

Вычитая предыдущие равенства друг из друга, приходим к уравнению

A ( x - xо) + B( y - yо) + C(z - zo) = 0,

(7.3)

которое можно интерпретировать как равенство нулю скалярного произведения век­торов n ¯ = (A, B, C) и MqM = ( x - x о,y - yo,z - z q). Таким образом, уравнению удовлетворяют в точности те точки M, для которых вектор MqM нернендикулярен вектору n ¯.

Задача 37. Составить уравнение плоскости, проходящей через точку (5,7,-3) пер­пендикулярно вектору (4,-6,8).

Решение. Уравнение (7.3) является решением задачи: составить уравнение плос­кости, проходящей через точку (xo,yo,zo) перпендикулярно вектору (A, B, C). Оста­ется подставить нап1и данные:

4(x - 5) - 6(y - 7) + 8(z + 3) = 0. Далее мож;но раскрыть скобки и привести подобные.

Если хотя бы один из коэффициентов A, B или C равен нулю, то уравнение плос­кости называют неполным. Например, если C = 0, то вектор n ¯ = (A, B, 0) параллелен плоскости XY, и значит, сама прямая параллельна оси Z.

August 31, 2013 Курбатов В.Г. 60

August 31, 2013 Курбатов В.Г. 61

и условие перпендикулярности

A1·A2 + B1·B2 + C1·C2 = 0 двух плоскостей.