7.6 Кривые 2-го порядка, их общее уравнение

Уравнением 2-го порядка называют уравнение вида

a11x2 + 2a12xy + a22y2 + 2b1x + 2b2y + c = 0.

Линию, задаваемую уравнением 2-го порядка, называют кривой 2-го порядка.

При замене координат уравнение может упрощаться. Путем поворота системы координат моясно добиться того, чтобы a12 = 0, а путем сдвига, как правило, допол­нительно — чтобы b1 = b2 = 0. Получающееся уравнение называют каноническим.

Нормальным уравнением окружности называют уравнение

x

y²

R².

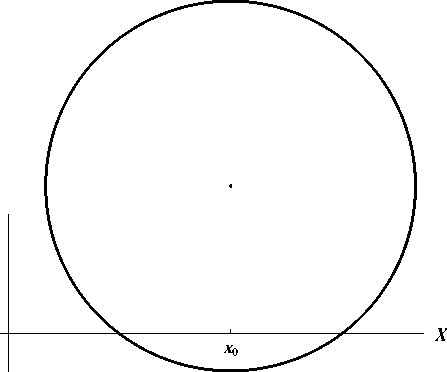
Оно задает окружность радиуса R с центром в начале координат. Сдвигая начало координат в точку ( x ₀,y ₀), получаем уравнение

( x - x ₀)2 + ( y- y ₀)² = R ².

Правило. Кривая F(x - x ₀ ,y - y ₀ ) = 0 получается из кривой F(x,y) сдвигом вправо на x ₀ и сдвигом вверх на y ₀-

Xy₀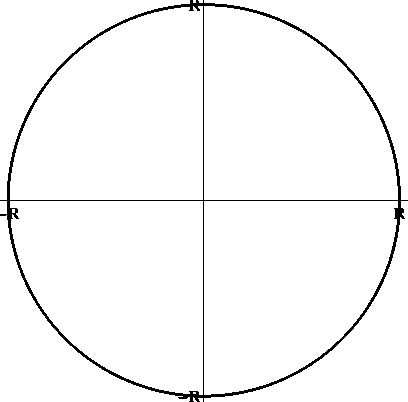

Рис. 4: Окруж;ности

August 31, 2013 Курбатов В.Г.

54

Задача 32. Изобразить кривую (x - 5)2 + (y + 3)2 = 4.

Решение. Это — окруясность, получающаяся из окружности x ² + y2 = 4 путем сдвига па вектор (5, -3). Окружность x² + y² = 4 имеет радиус 2. П

X

X

-1

-3

Рис. 5: Окруж;ности

7.7 Выделение полного квадрата

Полным квадратом называют выраж;ение

поскольку его можно преобразовать к виду (a + b)2. Выделение полного квадрата — важная процедура при построении кривых второго порядка. Например, уравнение

ax ² + ay ² + 2bix + 2b2y + c = 0,

называемое общим уравнением окружности, всегда можно привести к виду

(x - xо)2 + (y - yо)2 = R ².

Задача 33. Выделить полный квадрат в выраж;ении x2 - 6x + 5.

Решение. Имеем

x2 - 6x + 5 = x2 - 2x · 3 + 32 - 32 + 5

= (x2 - 2x · 3 + 32) - 4 = (x - 3)² - 4.

Такое преобразование удобно, например, для построения графика функции y = x2

6x + 5. -

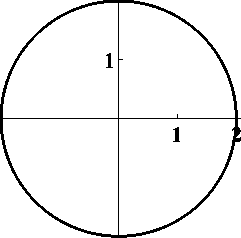
Задача 34. Построить кривую x2 - 10x + y ² + 6y + 30 = 0.

August 31, 2013 Курбатов В.Г.

55

Решение. Выделяем полные квадраты:

Получилось уравнение из задачи 32.

x² - 10x + y² + 6y + 30 = 0

x² - 2x · 5 + y² + 2y · 3 + 30 = 0

x² - 2x · 5 + 5² - 5² + y² + 2y · 3 + 3² - 3² + 30 = 0

(x² - 2x · 5 + 5²) + (y² + 2y · 3 + 3²) + 30 - 5² - 3² = 0

(x - 5)² + (y + 3)² - 4 = 0.

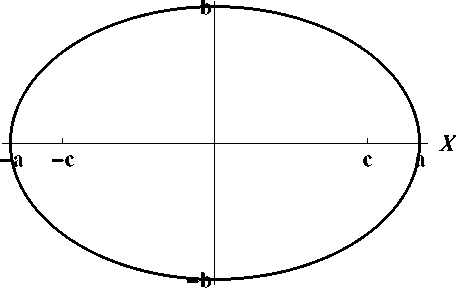
7.8 Эллипс

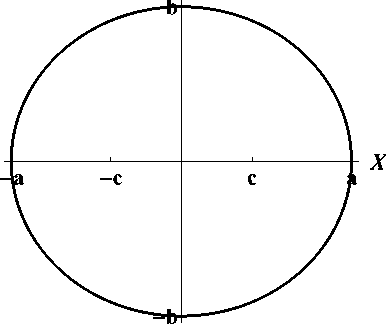
Эллипсом называют кривую, заданную уравнением

x² y²

+ a² b²

1.

А само уравнение называют каноническим уравнением эллипса. Числа a иb называ­ют полуосями, а точки пересечения с осями — вершинами.

Точки с координатами (c, 0) и (—c, 0), где c = ^a"^ — b^, называют фокусами.

Рис. 6: Эллипсы

Задача 35. Определить вид и расположение кривой x^ — 6x + 4y^ — 16y + 21 приведя ее уравнение к каноническому виду.

= 0,

August 31, 2013 Курбатов В.Г.

56

Решение. Выделяем полные квадраты:

х² -6х + 4 ² - 16у + 21 = 0

ж² - 2ж · 3 + 4(у2 - 2 · у · 2) + 21 = 0

ж2 - 2ж · 3 + 32 - 32 + 4(у2 - 2 · у · 2 + 22 - 22) + 21 = 0

(х2 -2х·3 + 32) + 4(у2 - 2 · у · 2 + 22) + 21 - 32 - 4 · 22 = 0

(ж-3)2 + 4(у-2)2-4 = 0

22 12

Получился эллипс с центром в точке (3,2) и полуосями 2 и 1. В качестве вспомо­гательного построения сначала рисуем прямоугольник с нужными полуосями. П

X

Рис. 7: Эллине из задачи 35