Глава 7

Элементы аналитической геометрии

7.1 Уравнение линии на плоскости

с интуитивной точки зрения линия — это след, оставляемый двиясущейся точкой.

Уравнением линии называют уравнение, которому удовлетворяют координаты каясдой точки, нринадлеясащей данной линии, но не удовлетворяют координаты лю­бой точки, не иринадлеясатдей данной линии. Например, y = x"^, x^ + y^ = 1.

Правило: Чтобы проверить, иринадлеясит ли точка липни, надо координаты точки подставить в уравнение линии.

Различают два тина уравнений:

y = f(x), (7.1)

F(x,y) = 0. (7.2)

Примеры таких уравнений:

y = e^x, x^ + y^ = 1.

В уравнении (7.1) неизвестная y явно выраясена через x. Такой способ задания назы­вают явным. Чтобы, зная x, с помощью уравнения (7.2) найти y, надо это уравнение решить. Такой способ задания называют неявным.

Правило: чтобы найти точку (точки) пересечения двух линий, надо выписать систему, состоящую из уравнений этих линий, и решить ее.-*-)

7.2 Уравнение прямой с угловым коэффициентом

Уравнением прямой с угловым коэффициентом называют уравнение вида

y = kx + b.

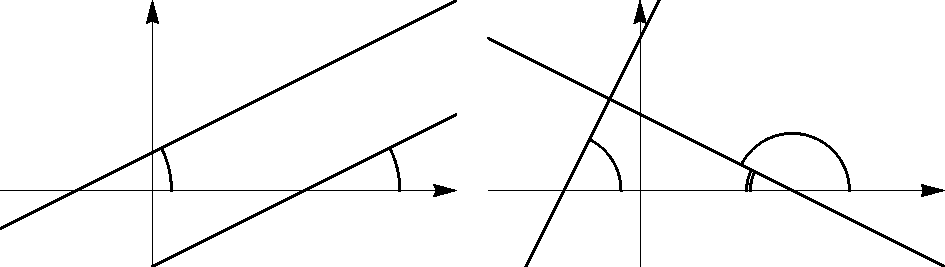
В нем коэффициент k имеет геометрический смысл тангенса угла меясду осью X и прямой.^) Число k называют угловым коэффициентом прямой. Если k > 0, то

August 31, 2013 Курбатов В.Г.

50

Рис. 1: Слева: k > 0; справа k < 0

график прямой возрастает. А если k < 0, то график прямой убывает. Число b имеет геометрический смысл координаты точки пересечения прямой с осью Y.

Правило: Угловой коэффициент — это то, па что умножается x в явном уравне­нии прямой. Примеры: 2y + 4x = 6 и y = —2x + 3.

■•■^Часто это правило формулирует не виолне корректно: надо приравнять у. Это путь можно реализовать только при условии, что оба уравнения являются явными. ■^Ютсчитываемого в нанравлении от оси к прямой.

August 31, 2013 Курбатов В.Г.

51

Задача 29. Составьте уравнение прямой, проходящей через заданную точку ( xо,yо) с заданным угловым коэффициентом k.

Решение. Ответом является уравнение

y - y₀ = k(x - x₀).

Эту формулу надо знать наизусть.

7.3 Общее уравнение прямой

Не все прямые можно задать уравнением с угловым коэффициентом. А именно, исключением является вертикальная прямая (см. рис. 2):

x = a.

Общим уравнением прямой называют уравнение

Ax + By + C = 0

в предположении, что хотя бы одно из чисел A, B не равно нулю. Это уравнение охватывает все типы прямых.

Рис. 2: Вертикальная прямая

7.4 Уравнение прямой,

проходящей через две заданные точки

Задача 30. Составьте уравнение прямой, проходящей через две заданные точки ( xо,yо) и (xi,yi).

August 31, 2013 Курбатов В.Г.

52

Решение. Ответом является уравнение

y -y₀

x-x₀

y₁ -y₀ x₁ -x₀

Универсальный способ построения прямых: надо нарисовать две точки, лежащие на прямой, и провести через них прямую.

7.5 Условие параллельности

и перпендикулярности прямых

Теорема 38. Пусть даны две прямые y = kix + bi и y = k2x + b ₂- Для того чтобы эти прямые были параллельны, необходимо и достаточно, чтобы

k₁ =k₂.

Для того, чтобы прямые были перпеидикуляриы, необходимо и достаточно, чтобы

k₁k₂

1.

Рис. 3: Идея доказательства теоремы 38

Задача 31. Дана прямая 2y + 3x —7 = 0. Составьте уравнения двух прямых, проходя­щих через точку (5,9), одна из которых параллельна, а другая — перпендикулярна исходной.

Решение. Выясним, какой угловой коэффициент у исходной прямой: (Угловой ко­эффициент — это то, на что умножается x в явном уравнении прямой.)

37 y = -2x + 2,

k₁ =

Выпишем уравпепие параллельной прямой (используя задачу 29: y — yо = k( x

xо)):

y - 9 = -2(x - 5).

August 31, 2013 Курбатов В.Г.

53

Выпишем уравнение иернендикулярной прямой (используя условие перпендикуляр­ности k1k2 = -1):

2 y-9 = -( x-5).

П