Глава 4

Арифметическое векторное пространство

4.1 Основные понятия

Если в трехмерном пространстве фиксированы декартовы координаты, его при­нято обозначать символом М.^. Аналогичным образом плоскость называют двумер­ным пространством и обозначают Е². Одномерное пространство Е^ — это ось. В этом параграфе мы рассмотрим абстрактное n-мерпое пространство Мⁿ, обобщающее Е^ Е2 и Е^

Упорядоченный набор из n чисел (xi; x2;... ;x_n) называют n-мерным (арифме­тическим) вектором, или просто вектором, или точкой и обозначают x ¯. Арифме­тический вектор обычно записываются в виде столбца или строки. Таким образом, арифметический вектор мояспо представлять себе как матрицу-столбец или матрицу-строку. Числа xi, i = 1,2,... ,n, называют компонентами или координатами векто­ра. Мпож;ество всех n-мерпых векторов называют n-мерным арифметическим про­странством, и обозначают Еⁿ.

Следующие определения совпадают с аналогичными определениями для матриц. Векторы x ¯ = (xi; x2;...; x_n ) и y ¯ = (yi; y2;...; y_n ) называют равными, если xi = yi, x2 = y2, ..., x_n = y_n- Суммой векторов x ¯ я y ¯ называют вектор x ¯ + y ¯ = (xi + yi; x2 + y2; . . .; x_n + y_n)- Аналогично определяют разность. Произведением числа λ и вектора x ¯ называют вектор λx ¯ = x ¯λ= (λxi; λx2;...; λx_n). Ср. с теоремой 11.

Нулевым называют вектор ¯0 = (0; 0;...; 0), имеющий пулевые координаты. Оче­видны тождества x ¯ — x ¯ = ¯0,x ¯ + 0 = x ¯ — 0 = x ¯, λ ¯0 = ¯0, 0-x ¯ = ¯0.

Теорема 18. Операции слоукеиия и умноукения на число обладают свойствами:

1. x ¯ + y ¯ = y ¯ + x ¯.

2. ( x ¯ + y ¯) + z = x ¯ + ( y ¯ + z).

1. Имеется такой вектор ¯0, что x ¯ + ¯0 = x ¯ для всех x ¯.

2. Для любого x ¯ существует такой вектор —x ¯, что x ¯ + (—x ¯) = ¯0.

3. 1x ¯ = x ¯.

4. α( βx ¯) = (αβ)x ¯.

5. (α + β)x ¯ = αx ¯ + βx ¯.

6. α( x ¯ + y ¯) = αx ¯ + αy ¯.

August 31, 2013 Курбатов В.Г. 37

Оказывается, подавляющее большинство свойств пространства Мⁿ является след­ствием только этих 8 свойств. Более того, имеется много других примеров мноясеств X, на которых определены операции слоясепия и умножения на число, для которых эти свойства выполняются. Например, мпоясество всех многочленов или множество всех функций с общей областью определения. Всякое такое множество X называ­ют векторным (линейным) пространством, а эти 8 свойств — аксиомами липейпого пространства. Для любого линейного пространства имеет смысл вся дальнейшая тео­рия.

4.2 Линейная независимость

Возьмем в линейном пространстве X систему из k векторов x ¯₁, x ¯2, ..., x ¯k- Всякий вектор вида

α1x ¯₁ + α2x ¯2 + · · · + αkx ¯k,

где α1, α2,.. ■, αk — числа, называют линейной комбинацией векторов x ¯1, x ¯2, ..., x ¯k-

Систему векторов называют линейно зависимой, если можно подобрать числа α1,

α2,..., α_k так, чтобы пе все опи были равны нулю и ири этом выполнялось равенство

α1x ¯₁ + α2x ¯2 +···+ αkx ¯k = 0. (4.1)

Для системы, состоящей из двух геометрических векторов, линейная зависимость означает, что векторы коллипеарны. Для системы, состоящей из трех геометриче­ских векторов, липейпая зависимость означает, что векторы леж;ат в одной или па параллельных плоскостях.

Систему векторов называют линейно независимой, если она не является линейно зависимой, т. е. если равенство (4.1) возможно только при условии, что α1 = α2 =

= α_k = 0. Эти определения дословно переносятся на матрицы-строки и матрицы-···лбцы.

Теорема 19. Система векторов x ¯1, x ¯2,..., x ¯k линейно зависима тогда и только тогда, когда один из векторов системы моукно представить в виде линейной комбинации остальных векторов.

Теорема 20. Ранг матрицы равен максимальному числу ее линейно независимых строк {столбцов).

Задача 24. Найти (максимальное) число линейно независимых среди следующих век-торов: (1,0,1), (2,1,3), (3,-1,2), (4,2,6).

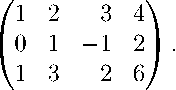
Из примера 14: ранг этой матрицы равен 2. Поэтому в ней два линейно независимых столбца. П

Решение. Составим из этих векторов матрицу:

August 31, 2013 Курбатов В.Г.

38