3.3 Декартова система координат

Декартовой}-> {прямоугольной) системой координат в пространстве называют

■"■^Декарт знаменит, например, своим высказыванием: "Я мыслю, значит, я существую".

August 31, 2013 Курбатов В.Г.

31

Рис. 3: Проекция вектора на ось

систему, состоящую из начальной точки O, трех взаимно ортогональных осей X, Y и Z, проходящих через точку O, и единичного отрезка, являющегося эталоном измерения. Аналогично определяется декартова система координат па плоскости.

Координатами вектора ¯ a относительно декартовой системы координат называют числовые проекции x, y и z вектора a ¯ на оси X, Y я Z соответственно, x называют абсциссой, y — ординатой иz — аппликатой.

Рассмотрим в пространстве произвольную точку A (см. рис. 4). Вектор ¯ a = O A называют радиус-вектором точки A. Координатами точки A называют координаты радиус-вектора O A .

Координаты вектора принято записывать через знак равенства, а координаты точки — около точки: ¯ a = (x; y; z), A(x; y; z).

Теорема 11. Пусть a ¯ = (a1; a2; a3) и¯ b = (b1; b2; b3)- Тогда

1. ¯ a + ¯ b= (a1 + b1; a2 + b2; a ₃ + b ₃);

1. λa ¯ = (λa1; λa2; λa ₃).

Доказательство. Вытекает из теоремы 10. Докажем, к примеру (а). Пусть c ¯ = a ¯ + ¯ b. Имеем x_c = пр_X c ¯ = пр_X(a ¯ + ¯ b) = пр_X a ¯ + пр_X b = a1 + b1. Аналогично y_c = a2 + b2

и zc = a ₃ + b ₃- □

Замечание 3. Геометрически очевидно, что векторы a ¯ = (a1; a2; a3) и ¯ b = (b1; b2; b ₃) параллельны (коллинеарны), если для некоторого λ выполняется равенство a ¯ = λ ¯ b. Пли в координатной форме:

(a1; a2; a ₃) = (λb ₁; λb2; λb ₃). Для существования такого λ необходимо и достаточно, чтобы совпали три числа:

a1

a2

a3

b ₃ .

August 31, 2013 Курбатов В.Г.

32

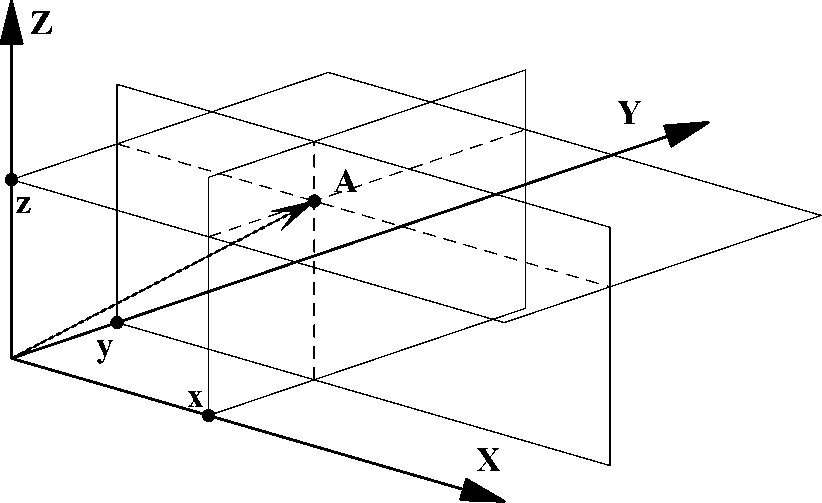
Рис. 4: Нахождение координат точки A в декартовой системе координат.

Это равенство называют условием параллельности векторов.

Задача 13. Являются ли векторы a ¯ = (2; 1; 3) и ¯ b = (—3; 3; 1) параллельными?

Решение. В силу замечания 3 для параллельности векторов должны выполняться

равенства

2 = 1 = 3

^31 . Видно, что это не так. Следовательно, векторы a ¯ и ¯ b не являются коллинеарными. П

Ортами или базисными векторами^ соответствующими данной декартовой систе­ме координат, называют единичные векторы ¯ i, j и k ¯, имеющие те же направления, что и оси координат X, Y и Z, соответственно. Очевидно, что ¯ i = (1; 0; 0), j = (0; 1; 0) и k ¯= (0;0;1).

Теорема 12. Любой вектор a ¯ = (x; y; z) моукно представить в виде суммы

a ¯ = x ¯ i + yj + zk. (3.1)

Эту формулу называют разложением вектора a ¯ по базисным векторам i, j, k ¯.

Доказательство. Действительно, xi + yj + zk = x(1; 0; 0) + y(0; 1; 0) + z(0; 0; 1) = ( x; 0; 0) + (0; y; 0) + (0; 0; z) = ( x; y; z) = a ¯. П

August 31, 2013 Курбатов В.Г. 33

3.4 Скалярное произведение

Скалярным произведением двух векторов a ¯ и b называют число, равное произве­дению длин векторов иа косин¯с угла между ними. Скалярное ироизведеиие векторов a ¯ и b обозначают символом a ¯ ■ b или {a ¯, ¯ b). Таким образом,

(a ¯, b) = |a ¯| ■ \¯\ cosω.

Замечание 4. Учитывая, что нр_{¯ b} ¯ a = |a|cosω и нр_{a ¯} ¯ b = |b|cosω, скалярное произве­дение моясно такясе определить, используя проекции. А именно,

(a ¯, ¯ b) = |¯ a| пр_{a ¯} ¯ b = |¯ b| нр_{¯ b} a ¯. (3.2)

Перечислим основные свойства скалярного произведения.

Ф (a ¯, ¯ b) = (¯ b, a ¯),

Ф (a ¯, ¯ b + c ¯) = (¯ a, ¯ b) + (¯ a, c ¯),

Ф (a ¯,λ ¯ b) = (λ¯ a,¯ b) = λ(¯ a,¯ b).

Ф Если векторы a ¯и¯ b ненулевые, то (a ¯, ¯ b) =0 тогда и только тогда, когда векторы ¯ a и¯ b ортогональны.

Напомним, что векторы a ¯и¯ b называют ортогональными^ если угол меясду ними равен π/2.

3.5 Выраж:ение скалярного произведения через координаты

Лемма 13. Для всевозмож.ных скалярных произведений базисных векторов i, j и k ¯

имеем i-i=j-j = k-k=1Hi-j = i-k ¯ = j-k = 0.

Теорема 14. Скалярное произведение двух векторов a ¯ = (a1; a2; a3) и¯ b= (b1; b2; b ₃) мож.ет быть вычислено но формуле

{a ¯, b) = a1b1 + a2b2 + a3b3.

Задача 14. Найти скалярное произведение векторов a ¯ = (1; 2; -3) и ¯ b = (0; 1; 2). Решение. В силу теоремы 14 имеем (a ¯, ¯ b) = 1 • 0 + 2 • 1 + (-3) -2 = 2-6 = -4. П Следствие 15. Длина вектора ¯ a = (a1; a2; a3) моукет быть вычислена но формуле

|a ¯| = a²₁ + a ²2 + a²₃.

Задача 15. Найти длину |a ¯| вектора a ¯ = (2; -2; 1).

Решение. В силу следствия 15 длина |a ¯| вектора ¯ a = (2; -2; 1) равна -\/4 + 4+1 = V9 = 3. П

August 31, 2013 Курбатов В.Г. 34

Задача 16. Найти длину вектора 3a ¯ - 2¯ b, где a ¯ = (1; 2; 3), b = (4; -5; 0). Решение. Сначала найдем координаты вектора 3a ¯ - 2¯ b:

3¯ a - 2b =3 • (1; 2; 3) - 2 • (4; -5; 0) = (3; 6; 9) - (8; -10; 0) =(3 - 8; 6 + 10; 9 - 0) = (-5; 16; 9).

Тенерв найдем длину этого вектора в соответствии со следствием 15:

|3¯ a - 2b| =Ja²₁ + a²₂ + a²

= (-5)² + 162 + 92 = V25 + 256 + 81 = л362 ^ 19. П

Пусть дан ненулевой вектор a ¯. Рассмотрим вектор e ¯ = _| ^a _a|. Покаясем, что он имеет длину, равную 1. Действительно, |e ¯| = |_| ^a_{a |}| = |_a ¹_||¯ a| = 1- Очевидно, вектор e ¯ имеет то же направление, что и вектор a ¯. Переход от вектора ¯ a к вектору e ¯ = _| ^a _a| называют нормированием вектора a ¯.

Задача 17. Нормируйте вектор a ¯ = (5; -6; 7).

Решение. Имеем

|a ¯| = л/52 + (-6)2 + 72 = V25 + 36 + 49 = v110.

Поэтому

e ¯= a ¯ = (5;-6; 7) = ^ 5 -6 ; 7 ч ^

|a ¯| ^110 v110 ;v110v110 .

Следствие 16. Расстояние меукду точками A(a1;a2;aз) и B(b1;b2;bs) моукет быть вычислено по формуле

|AB| = х/(b1 - a1)2 + (b2 - a2)2 + (bз - aз)2. (3.3)

Доказательство. Пусть a ¯ = AB. Тогда a ¯ = OB - OA = (b ₁ - a1; b2 - a2; bз - aз). Отсюда

|AB| = |¯ a| = л( b ₁ - a1)2 + (b2 - a2)2 + (bз - aз)2.

П Задача 18. Найти длину |AB| отрезка AB, где A(1; 0; 3) и B(0; 2; 1). Решение. В силу формулы (3.3) имеем

|AB| = v/(0-1)2+ (2-0)2+ (1-3)2 = 3. П

Задача 19. Даны векторы ¯ a = (2; -1; 3), ¯ b = (4; 0; -3). Найти (а) ¯ a- ¯ b, (Ь) |3a ¯ - 2¯ b|, (с) нормировать векторы ¯ a и ¯ b.

Ответ: (а) -1; (Ь) v/238; (с) e ¯ _a = (-²₁, ^, -^), e ¯ _b^ = (0, 8; 0; -0, 6).

August 31, 2013 Курбатов В.Г.

35

3.6 Угол меж:ду двумя векторами

Теорема 17. Косинус угла ω меукду

a ¯ = (a1; a2; a3) и b = (b1; b2; b ₃) мож.ет быть найден по формуле

векторами

(3.4)

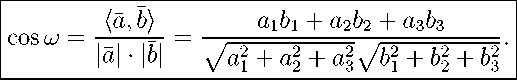
Замечание 5. Если ¯ a • ¯ b = 0, то из формулы (3.4) видно, что cosω = 0. Поэтому равенство

a1b1 + a2b2 + a3b3 = 0

называют условием перпендикулярности (ортогональности) векторов. Ср. со свой­ством 4 скалярного произведения.

Задача 20. Найти угол между векторами a ¯ = (1; 2; 5) и ¯ b = (-1; 3; 0).

Решение. Воспользуемся формулой (3.4). Имеем

1-(-1) + 2-3 + 5-0 5 1

cos ω

V1+ 4 +25 V1+ 9 + 0 V300 2V3

ω

arctg

1

2V3

Задача 21. Найти косинус угла ABC треугольника ABC, где A(2;-3;0), B(3; 1; 2), C(1;-2;4).

Решение. Угол ABC можно интерпретировать как угол между векторами a ¯ = BA = (2; -3; 0) - (3; 1; 2) = (2 - 3; -3 - 1; 0 - 2) = (-1; -4; -2), b = BC = (1; -2; 4) - (3; 1; 2) = (1 - 3; -2 - 1; 4 - 2) = (-2; -3; 2).

Косинус угла меж;ду векторами найдем но формуле (3.4):

(¯ a,b) (-1).(-2) + (-4).(-3) + (-2).2

cosω =

¯ a ■ \b\ ^(-1)2 + (-4)2 + (-2)2^(-2)2 + (-3)2 + 22 2 + 124 10 10

V1

16 + 4V4 + 9 + 4 V21 • 17 V357

Задача 22. Являются ли векторы a ¯ = (2; 1; 3) и ¯ b = (-3; 3; 1) перпендикулярными?

Решение. Воспользуемся замечанием 5 и найдем скалярное произведение:

(¯ a, b) = 2 • (-3) + 1-3 + 3-1 = -6 + 3 + 3 = 0.

Следовательно, векторы a ¯ и ¯ b нернендикулярпы. П

Задача 23. Составить уравнение прямой, проходящей через точку (x ₀,y ₀) нерненди-кулярно вектору (A, B).

Решение. Ответ задается формулой

A( x - x ₀) + B( y - y ₀) = 0.

Действительно, это равенство означает нерпендикулярпость вектора ( x - x ₀,y - y ₀), лежащего на прямой, вектору (A, B). П