Конспект по линейной алгебре

Виталий Геннадьевич Курбатов

31 августа 2013 г.

_{Оглавление}

1 Матрицы и определители 3

1. Матрицы 3

2. Операции над матрицами 4

3. Определители второго порядка 6

4. Определители третьего порядка 7

5. Свойства определителей 8

6. Символ суммирования 9

7. Миноры и алгебраические донолнепия 9

8. Определители гг-го порядка 10

9. Метод элементарных преобразований вычисления определителя .... 10

10. Ранг матрицы 11

11. Метод элементарных преобразований вычисления ранга 12

12. Обратная матрица и ее нахоясдение методом ирисоединенной матрицы 13

2 Системы линейных уравнений 15

1. Основные понятия 15

2. Метод Крамера 16

3. Матричная запись системы линейных уравнений 18

4. Метод обратной матрицы 19

5. Матричные уравнения 20

6. Метод Гаусса 20

7. Несовместная система 24

8. Неопределенная система 25

9. Система линейных однородных уравнений 27

10. Понятие о модели Леонтьева 28

3 Векторы в трехмерном пространстве 29

1. Основные понятия 29

2. Числовая проекция вектора 30

3. Декартова система координат 30

4. Скалярное произведение 33

5. Выраж;ение скалярного произведения через координаты 33

6. Угол меясду двумя векторами 35

4 Арифметическое векторное пространство 36

1. Основные понятия 36

2. Линейная независимость 37

August 31, 2013 Курбатов В.Г. 2

3. Размерность и базис 38

4. Скалярное произведение в гг-мерном иространстве 39

5. Ортогональные векторы 40

5 Линейные операторы 41

1. Понятие линейного оператора 41

2. Матрица линейного оператора 41

3. Собственные значения и собственные векторы 43

6 Квадратичные формы 45

1. Определение квадратичной формы, ее матрица 45

2. Канонический вид и закон инерции 46

3. Знакоонределенные квадратичные формы 47

7 Элементы аналитической геометрии 49

1. Уравнение линии на плоскости 49

2. Уравнение прямой с угловым коэффициентом 49

3. Общее уравнение прямой 51

4. Уравнение прямой, проходящей через две заданные точки 51

5. Условие параллельности и нернендикуляриости прямых 52

6. Кривые 2-го порядка, их общее уравнение 53

7. Выделение полного квадрата 54

8. Эллипс 55

9. Гипербола 56

10. Парабола 58

11. Уравнение плоскости 58

12. Уравнение прямой 61

Глава 1

Матрицы и определители

1.1 Матрицы

Матрицей называют прямоугольную таблицу, состоящую из чисел. Для краткого обозначения матриц обычно используют латинские буквы A,B,C,.... Например,

1. 2 14 7' A= \ -1 2 -3 -2

1. 8 9 0,5

В матрицах выделяют строки и столбцы.

Когда говорят о произвольной матрице, ее обычно записывают в виде

A=

a11 a12 . . . a1n a21 a₂₂ . . . a2_n

am1 am2 . . . a_mn

Числа aij называют элемеитами матрицы. Заметим, что элементы матрицы a_{i 1}, a_{i 2}, имеющие одинаковый первый индекс i, образуют i-ю строку матрицы. Аналогично, элементы a1j, a2j, . . ., amj образуют j-ый столбец. Таким образом, первый индекс i в обозначении a_ij совпадает с номером строки, а второй j — с номером столбца.

Если хотят подчеркнуть, что матрица A состоит из элементов a_ij, то пишут A = {aij}.

Выраж;еиие-'-) m × n называют размером матрицы. Например, у матрицы

/ 1 2 14 7' A= -1 2 -3 -2 \ 2 8 9 0,5

размер 3×4.

Две матрицы A = {aij} и B = {b_ij} считают равными, если совпадают их размеры и равны соответствующие элементы, т. е. a_ij = b_ij для всех i я j.

^^ Говоря "выражение" вместо "число", имеют в виду, что умножение в конструкции т×п остается невыполненным.

August 31, 2013 Курбатов В.Г.

Если m = n, то матрицу называют квадратной, а если m = n , то — просто прямоугольной.

Пусть A — квадратная матрица. Ее главной диагональю или просто диагональю называют множество элементов a₁₁, a22, •••, a_nn, имеющих одинаковые индексы, т. е. главная диагональ идет из левого верхнего угла в правый нижний, а побочная диагональ — из левого ниж;него угла в правый верхний.

Квадратную матрицу называют диагональной, если все ее элементы, стоящие вне главной диагонали, равны пулю:

fd1 0 ... 0\ 0 d ₂ ... 0

00

d

Например,

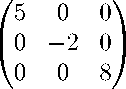
Если все di равны 1, то матрицу называют единичной и обозначают буквой E, а если все di равны О, то — нулевой и обозначают буквой O:

0 0

E=

10 01

0 0 ... 1

O=

0 0

0 0 0 0

0 0

Например,

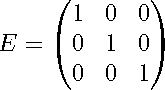
E=

10 01

Матрицу называют треугольной (или, подробнее, верхне-треугольной), если все ее элементы, стоящие ниж;е главной диагонали, равны нулю:

a11 a12 0a₂₂

a1n a2n

0

0

Например,