Системы координат. Определение положения точки на Земной поверхности .

Для определения положения точки на земной поверхности математического описания гравитационного поля Земли используют в основном две системы координат :

1. Геоцентрическая .

Положение точки М на поверхности эллипсоида Красовского определяют две координаты :

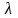(долгота) –угол между плоскостью Гринвичского меридиана и плоскостью местного меридиана ,проходящего через точку М .

Долготы точек расположенные восточнее Гринвичского меридиана принято считать положительными ,а западнее – отрицательными .

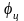(геоцентрическая широта) – угол между экватором и радиусом проведенным из центра эллипсоида через точку М .

Широты лежащие выше экватора (северные) – положительные , а южные – отрицательные .

2. Геодезическая .

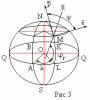В этой системе положение точки на поверхности эллипсоида Красовского также определяются по двум координатам :

(долгота) – определяется аналогична предыдущей .

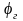(геодезическая широта) – плоскостью экватора и нормалью к поверхности эллипсоида в точке М .

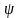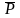Геодезическим азимутом направления L называется угол , отсчитываемый по часовой стрелке от северного направления геодезического меридиана от данной точки до заданного направления .

и связаны между собой следующим соотношением :

где е – эксцентриситет меридионального эллипса и общего земного эллипсоида .

Гравитационное поле Земли .

Согласно второму закону Ньютона (закон тяготения) каждая частица массой М притягивает другую частицу массой m силой гравитационного притяжения (тяготения) G_т , определяемой следующей зависимостью :

Где f – гравитационная постоянная ;

г – расстояние между частицами .

Если эту формулу применить к Земле , то 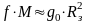- для приближенных расчетов .

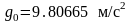- ускорение земного притяжения

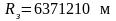
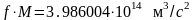
При полете ЛА , на них действуют силы притяжения Земли и других небесных тел . При полете ЛА на небольшом расстоянии от Земли действие небесных тел (Луна , Солнце и т.д.) незначительно или ими пренебрегают . Сила притяжения Земли консервативна , т.е. имеет силовую функцию .

G – зависит географической точки расположения (от долготы и широты) . Для удобства расчетов принимаем , что сила притяжения Земли G=const .

Атмосфера .

При полете ЛА на небольшом расстоянии от Земли , на него кроме силы тяжести действуют аэродинамические силы . Величина этих сил зависит от конструкции ЛА , а также от состояния параметров атмосферы (температура , плотность , давление) .

Параметры атмосферы в свою очередь зависят от :

• географической широты места полета ;

• времени суток ;

• времени года ;

• и т.д. (активности Солнца) .

При расчете траектории ЛА при его проектировании используются значения стандартной атмосферы ( СА ) , которые некоторые средние значения параметров спокойной атмосферы в зависимости от высоты полета . СА 1981 г. или ГОСТ 4401-81 даны параметры до высоты 200 км . В СА за нулевую отметку принят уровень моря . На нулевой отметке давление равно 760 мм.рт.ст. или 1.101 МПа , температура – 288⁰К (+15⁰С) . При этих условиях массовая плотность воздуха равна .

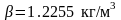Зависимость СА от высоты подобрана таким образом , что СА ближе всего подходит к средним широтам северного полушария в летнее время .

Отклонение параметров атмосферы от стандартных значений , а также ветер представляют собой атмосферные возмущения , которые влияют на полет ЛА .

При проектировании ЛА необходимо знать диапазоны возможных отклонений этих параметров , знать статистические зависимости между случайными отклонениями каждого параметра на разных высотах от времени года , географической широты и т.д.