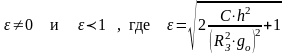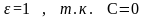- •Теория полета . Введение.
- •Движение , форма и гравитационное поле Земли . Движение Земли .
- •Форма Земли .
- •Системы координат. Определение положения точки на Земной поверхности .
- •Геоцентрическая .
- •Геодезическая .
- •Гравитационное поле Земли .
- •Атмосфера .
- •Уравнение движения точки переменной массы .
- •Теорема об изменении количества движения системы материальных точек .
- •Формула Циалковского .
- •Система координат .
- •Стартовая система координат
- •С коростная система координат (поточная)
- •Косинусы углов между связанными и скоростными осями .
- •Силы и моменты действующие на ракету в полете . Аэродинамические силы .
- •Особенности аэродинамических характеристик .
- •Аэродинамические моменты .
- •Положение центра давления .
- •Демпфирующий момент .
- •Управляющие силы и моменты .
- •Органы управления . Управляющие моменты .
- •Основные типы органов управления баллистических ракет .
- •В оздушные рули .
- •Комбинированные органы управления .
- •Сила реактивной тяги .
- •Реактивный момент .
- •Аэродинамические схемы ла .
- •Возмущающие силы и моменты .
- •Атмосферные возмущения .
- •Требования к траектории .
- •Расчет активного участка траектории бр методом последовательных приближений .
- •Метод последовательных приближений .
- •Поделим левую и правую часть уравнения 3 на массу m
- •Для решения необходимо сделать это уравнение с разделенными переменными
- •Рассмотрим выполнение программного угла θ .
- •Расчет пассивного (эллиптического) участка траектории . Постановка задачи .
- •Уравнение траектории пассивного участка .
- •З апишем уравнение энергии
- •Подставим в это уравнение
- •Уравнение с разделенными переменными
- •Уравнение эллиптического участка траектории . Частные случаи .
- •Время полета ракеты на эллиптической траектории .
- •Определение оптимального угла траектории в конце активного участка .
- •Рассмотрим п.1
- •Теория полета космических кораблей . Орбитальные движения тел . Законы Кеплера .
- •Движение тел , при таких условиях носит название орбитальное .
- •Первый закон Кеплера .
- •Второй закон Кеплера .
- •Третий закон Кеплера .
- •Вывод искусственного спутника Земли (исз) на орбиту без учета сопротивления атмосферы .
- •Кинематические уравнения , связанные с движением исз .
- •Исключим из уравнений (8) , (9) , (10) скорость Va и параметр р
- •Траектория полета космических кораблей . Общие замечания .
- •Оптимальные перемещения кк с одной круговой орбиты на другую .
- •Определение характеристической скорости двух импульсного оптимального маневра .
- •Двух импульсный перелет между компланарными круговыми орбитами . Формула Циалковского .
- •Методы наведения зенитных управляемых ракет (зур) .
- •Основные требования к методам наведения .
- •Э то такой метод наведения , при котором линия “ракета-цель” в течении всего времени полета ракеты остается параллельной самой себе .
Уравнение траектории пассивного участка .
Используем два полученных интеграла для вывода уравнений траектории пассивного участка .
Если точка движется в декартовой системе координат ОXY , то траектория имеет вид :
Y=f(x) , а в полярной системе координат : r =f(λ)
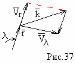

З апишем уравнение энергии
Запишем
момент количества движения
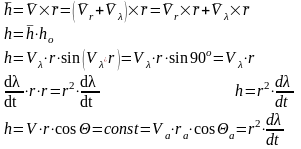
Имеется несколько неизвестных величин : r , t , λ .
Чтобы получить уравнение траектории нужно избавиться от величины t .
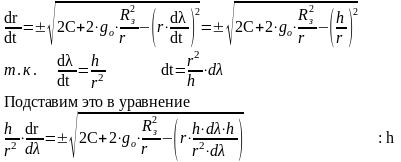
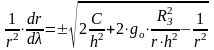 - дифференциальное
уравнение траектории пассивного участка
.
- дифференциальное
уравнение траектории пассивного участка
.
Выбор знака “ ± “ зависит от выбора направления отсчета угла λ .
Если угол λ отсчитывается по часовой стрелке , то ставится знак “ - “ и наоборот . Так на рис.36 угол λ по часовой стрелке , следовательно при расчете нужно ставить знак “ – “ .
Чтобы решить это уравнение нужно ввести новую переменную :

Тогда получим :
`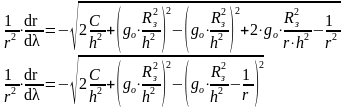
Подставим в это уравнение
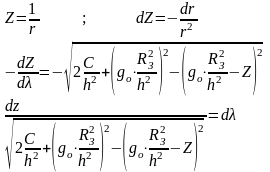
Уравнение с разделенными переменными
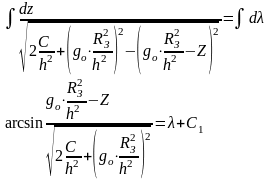
т.к. λ – это угол , то и С1 тоже угол . Обозначим φ=С1 .
Избавимся от arcsin и от дроби :
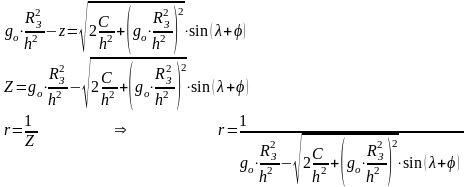
Извлечем
из под радикала выражение:
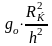 и поделим знаменатель на эту величину.
и поделим знаменатель на эту величину.
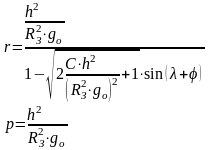
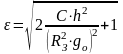 - эксцентриситет
траектории ;
- эксцентриситет
траектории ;
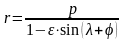 Можно
выбрать такое начальное положение
плоскости n-n
чтобы
Можно
выбрать такое начальное положение
плоскости n-n
чтобы
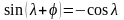
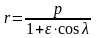 - уравнение
траектории полета ракеты на пассивном
участке.
- уравнение
траектории полета ракеты на пассивном
участке.
С точки зрения математики это уравнение которое образуется при пересечении конуса плоскостью (уравнение кривой).
Уравнение эллиптического участка траектории . Частные случаи .
Рассмотрим несколько случаев :
Плоскость перпендикулярна оси конуса .
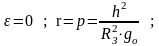
В сечении будет окружность , следовательно точка движется по окружности .
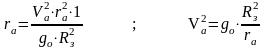
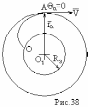
Необходимая скорость , которую должна получить ракета в точке А , чтобы она могла двигаться по орбите вокруг Земли , эту скорость принято называть первой космической скоростью.
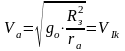 .
.
Это уравнение эллипса или эллиптическая траектория . В этом случае С<0 . Для этого случая запишем уравнение энергии :

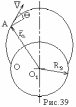 -
необходимое условие для получения
эллипса .
-
необходимое условие для получения
эллипса .
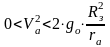 -
траектория эллипса .
-
траектория эллипса .
Случаи :
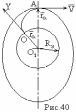 -
эллиптическая траектория ракеты класса
“Земля – Земля” (рис.39) .
-
эллиптическая траектория ракеты класса
“Земля – Земля” (рис.39) .
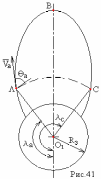
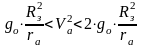 -
это орбитальный эллипс и его вытянутость
зависит от величины скорости в точке
А (рис.40) .
-
это орбитальный эллипс и его вытянутость
зависит от величины скорости в точке
А (рис.40) .
Уравнение энергии
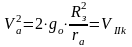 -
вторая космическая скорость .
-
вторая космическая скорость .
Приближенно можно считать , что VIk≈8 км/с , а VIIk≈11.2 км/с .
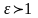 -
это траектория гиперболы при С>0 .
-
это траектория гиперболы при С>0 .
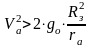
 -
гиперболическая скорость (третья
космическая скорость) .
-
гиперболическая скорость (третья
космическая скорость) .
Время полета ракеты на эллиптической траектории .
Уравнение траектории движения ракеты на эллиптическом участке
Запишем уравнение для момента количества движения точки единичной массы :
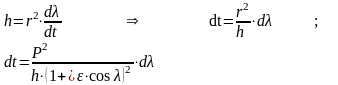
Проинтегрируем
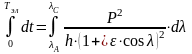
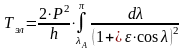 - время полета
ракеты на эллиптическом участке
траектории .
- время полета
ракеты на эллиптическом участке
траектории .
Добавляем “2” и интегрируем до π потому , что берем только половину траектории .
Это уравнение можно решить аналитическим методом или методом численного интегрирования .
Расчет участка снижения .
Допущения в расчетах :
масса спускаемого аппарата постоянна mСА=сonst ;
п
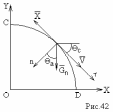 ренебрегаем
кривизной Земли и рассматриваем движение
в прямоугольных координатах ;
ренебрегаем
кривизной Земли и рассматриваем движение
в прямоугольных координатах ;ускорение свободного падения постоянно g=go=const ;
угол атаки равен нулю α=0 , следовательно и подъемная сила равна нулю
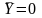 .
.
При расчете пассивного участка траектории мы должны получить дальность полета , время , коэффициенты перегрузок (продольные) .
yc=ya – высота
Θс=-Θа
Vc=Va
Xc=0 ( Xc=Xa+Lэл )
Уравнение движения ракеты будет :
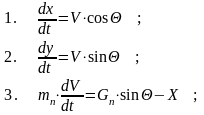

Эта система решается любым численным методом .