---------------------------------------------------------------------------------------------------------------------
ВОПРОС №13
Методы решения нелинейных уравнений. Метод хорд, условие его сходимости. Реализация методов в MATLAB.
---------------------------------------------------------------------------------------------------------------------
Методы решения нелинейных уравнений.
Методы решения нелинейных уравнений делятся на прямые и итерационные.
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений. Для решения же большинства встречающихся на практике уравнений используются методы последовательных приближений, т.е. итерационные методы.
Они предполагают, что известны достаточно малые окрестности, в каждой из которых имеется только один корень уравнения. Принимая за начальное приближение одну из точек этой окрестности, можно вычислить искомый корень с заданной точностью.
Таким образом, задача приближенного вычисления корней уравнения распадается на две:
отделение корней уравнения, то есть отыскание достаточно тесных промежутков, в каждом из которых содержится только один корень уравнения;
уточнение корней, то есть вычисление корня с заданной точностью, если известно некоторое начальное его приближение в области, не содержащей других корней.
Метод хорд.
Метод основан на замене функции f(x) на каждом шаге поиска хордой, стягивающей значения функции на концах отрезка [a,b]. Её пересечение с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b;
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a.
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой, получаемой из подобия треугольников:
для
случая а)
для
случая б)
Процесс поиска продолжается до тех пор, пока не выполнится условие
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и её кривизны f"(z) совпадают. Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.
Реализация метода:
Вот вам блок- схема
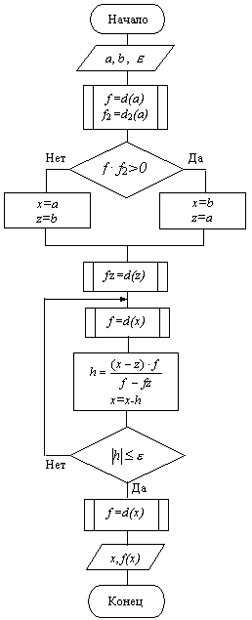
, да прибудет с вами сила)
--------------------------------------------------------------------------------------------------------------------ВОПРОС №14
Методы решения нелинейных уравнений. Метод Ньютона (метод касательных), условие его сходимости. Реализация методов в MATLAB.
Методы решения нелинейных уравнений.
Методы решения нелинейных уравнений делятся на прямые и итерационные.
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений. Для решения же большинства встречающихся на практике уравнений используются методы последовательных приближений, т.е. итерационные методы.
Они предполагают, что известны достаточно малые окрестности, в каждой из которых имеется только один корень уравнения. Принимая за начальное приближение одну из точек этой окрестности, можно вычислить искомый корень с заданной точностью.
Таким образом, задача приближенного вычисления корней уравнения распадается на две:
отделение корней уравнения, то есть отыскание достаточно тесных промежутков, в каждом из которых содержится только один корень уравнения;
уточнение корней, то есть вычисление корня с заданной точностью, если известно некоторое начальное его приближение в области, не содержащей других корней.
Метод Ньютона(касательных).
Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.
Он основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня.
Выберем начальную точку x0=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x1.
x1 = x0 – h0, f΄(x0) = tg(α), тогда
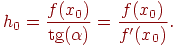
Поэтому
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой
(2)
Процесс
поиска продолжаем до тех пор, пока не
выполнится условие:
(1)
Подставим в условие (1) уравнение (2). Получим:
Метод обеспечивает быструю сходимость, если выполняется условие:
т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x0) и ее кривизны f"(x0) совпадают
а вот и блок- схема:
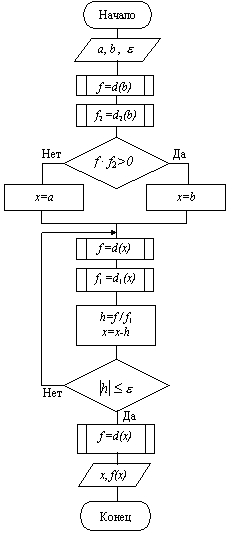
--------------------------------------------------------------------------------------------------------------------ВОПРОС №15
Методы решения нелинейных уравнений. Модифицированный метод Ньютона(метод секущих), условие его сходимости. Метод одной касательной. Реализация методов в MATLAB.
--------------------------------------------------------------------------------------------------------------------
Методы решения нелинейных уравнений.
Методы решения нелинейных уравнений делятся на прямые и итерационные.
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений. Для решения же большинства встречающихся на практике уравнений используются методы последовательных приближений, т.е. итерационные методы.
Они предполагают, что известны достаточно малые окрестности, в каждой из которых имеется только один корень уравнения. Принимая за начальное приближение одну из точек этой окрестности, можно вычислить искомый корень с заданной точностью.
Таким образом, задача приближенного вычисления корней уравнения распадается на две:
отделение корней уравнения, то есть отыскание достаточно тесных промежутков, в каждом из которых содержится только один корень уравнения;
уточнение корней, то есть вычисление корня с заданной точностью, если известно некоторое начальное его приближение в области, не содержащей других корней.
Метод Ньютона(секущих).
В этом методе производная на каждом шаге поиска вычисляется приближённо по результатам двух предыдущих итераций:
и рекуррентная формула имеет вид:
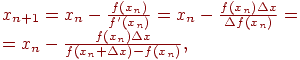
Выход из итерационного процесса по условию:
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приёмом Гарвика: выбирают некоторое εx и ведут итерации до выполнения условия
|xn+1-xn|≤ εx . Затем продолжают расчет, пока убывает |xn+1-xn| . Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.
Метод одной касательной.
Заметим, что в методе секущих удобно было бы фиксировать наиболее подходящее для первого шага значение
,
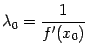при котором все секущие параллельны
касательной, проведённой к графику
y
= f(x)
при х = х0.
При
таком выборе метод секущих называется
методом одной касательной.
Итерационная формула этого метода имеет вид:
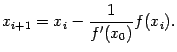
Как видно из этой формулы, производную придётся вычислить только один раз, а затем на каждом шаге использовать значение
или,
что то же,
.
При
таком выборе
в точке х0
выполнено равенство
и
если отрезок, на котором отделён корень
и выбрано начальное приближение х0
достаточно мал, а производная
непрерывна,
то значение
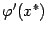будет
не сильно отличаться от
и,
следовательно, график y
= f(x)
будет пересекать прямую
y = x , идя почти горизонтально. А это будет давать нам быстрое приближение итераций к корню.
---------------------------------------------------------------------------------------------------------------------ВОПРОС №16
Методы решения нелинейных уравнений. Метод простых итераций, условие сходимости. Реализация методов в MATLAB.
---------------------------------------------------------------------------------------------------------------------
Методы решения нелинейных уравнений.
Методы решения нелинейных уравнений делятся на прямые и итерационные.
Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений. Для решения же большинства встречающихся на практике уравнений используются методы последовательных приближений, т.е. итерационные методы.
Они предполагают, что известны достаточно малые окрестности, в каждой из которых имеется только один корень уравнения. Принимая за начальное приближение одну из точек этой окрестности, можно вычислить искомый корень с заданной точностью.
Таким образом, задача приближенного вычисления корней уравнения распадается на две:
отделение корней уравнения, то есть отыскание достаточно тесных промежутков, в каждом из которых содержится только один корень уравнения;
уточнение корней, то есть вычисление корня с заданной точностью, если известно некоторое начальное его приближение в области, не содержащей других корней.
Метод простых итераций.
Пусть с точностью ε необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.
Для применения этого
метода исходное уравнение f(x)=0 должно
быть приведено к виду
.
Это преобразование можно сделать по разному и получить различного вида функции, в зависимости от вида f(x). Например, можно положить φ(x) = x + b * f(x)
где b = const, при этом корни исходного уравнения не изменятся. В качестве начального приближения 0 выбираем любую точку интервала [a,b]. Далее итерационный процесс поиска корня строится по схеме:
xn= φ(xn-1)
Процесс поиска
прекращается, как только выполняется
условие
или число итераций превысит заданное
число N.
Для того, чтобы
последовательность х1,
х2,…, хn
приближалась к искомому корню,
необходимо, чтобы выполнялось условие
сходимости:
При этом принято различать три вида сходимости:
|φ΄(x)|< 0,1 – хорошая сходимость;
0,1<|φ΄(x)|< 0,5 – удовлетворительная сходимость;
0,5<|φ΄(x)|< 1,0 – плохая сходимость.
---------------------------------------------------------------------------------------------------------------------ВОПРОС №17
Решение систем нелинейных уравнений. Метод простых итераций, условие сходимости итерационного процесса. Возможности MATLAB для решения систем нелинейных уравнений.
---------------------------------------------------------------------------------------------------------------------
Решение систем нелинейных уравнений.
В
отличие от систем линейных уравнений
для систем нелинейных уравнений
неизвестны прямые методы решения. При
решении систем нелинейных уравнений
используются итерационные методы.
Эффективность всех итерационных методов
зависит от выбора начального приближения
(начальной точки), т.е. вектора
.
Приступая к задаче решения системы нелинейных уравнений, необходимо убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение.
в случае системы двух уравнений с двумя неизвестными это можно сделать, построив графики функций в удобных координатах.
В случае сложных функций можно посмотреть поведение полиномов, их аппроксимирующих.
Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.
Метод простых итераций(условие сходимости итерационного процесса).
Для применения этого метода исходная система (1) должна быть преобразована к виду
Или
Далее,
выбрав начальное приближение
приближение
и используя систему, строим итерационный
процесс поиска по схеме:
т.е.
на каждом k-ом шаге поиска вектора
переменных находим
,
используя значения переменных, полученные на шаге (k-1).
Итерационный процесс поиска прекращается как только выполнится условие
При этом оно должно выполняться одновременно по всем переменным. Метод простых итераций используется для решения таких систем нелинейных уравнений, в которых выполняется условие сходимости итерационного процесса поиска, а именно:
т.е. сумма абсолютных величин частных производных всех преобразованных уравнений системы (2) по j-ой переменной меньше единицы. В более общей форме достаточное условие сходимости: метод простых итераций сходится к решению системы (2), если какая-либо норма матрицы Якоби, построенной по правым частям системы (2), меньше 1 на каждой итерации. Метод Зейделя имеет аналогичные условия сходимости.
Блок- схема:
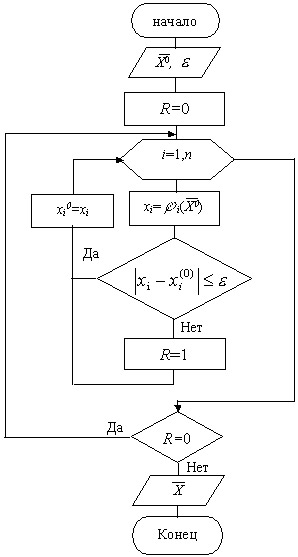
Возможности matlab для решения систем нелинейных уравнений.
Решение нелинейных уравнений и систем выполняется с помощью функции fsolve.
>> fsolve(< имя функции>, <начальное значение>,<опции>),
Где < имя функции> - имя М-функции, которая определяет левую часть уравнения f(x)=0 или системы уравнений F(x)=0: она должна принимать на входе вектор аргументов и возвращать вектор значений; <начальное значение> - вектор приближений, относительно которого будет осуществляться поиск решения.
Где <опции> - дополнительные параметры управления вычислительным процессом. Их можно определить с помощью функции
optimset (<вид контроля>, <значение>).
---------------------------------------------------------------------------------------------------------------------
ВОПРОС №18
Решение систем нелинейных уравнений методом Ньютона. Возможности MATLAB для решения систем нелинейных уравнений.
---------------------------------------------------------------------------------------------------------------------Решение систем нелинейных уравнений.
В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора .
Приступая к задаче решения системы нелинейных уравнений, необходимо убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение.
в случае системы двух уравнений с двумя неизвестными это можно сделать, построив графики функций в удобных координатах.
В случае сложных функций можно посмотреть поведение полиномов, их аппроксимирующих.
Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.
Метод Ньютона.
Дана система:
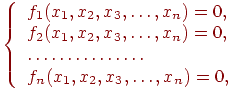
Метод Ньютона - наиболее распространенный метод решения систем нелинейных уравнений. Он обеспечивает более быструю сходимость по сравнению с методом итераций.
В основе метода Ньютона лежит идея линеаризации всех нелинейных уравнений системы Сообщим всей системе малые приращения hj и разложим каждое уравнение системы в ряд Тейлора:
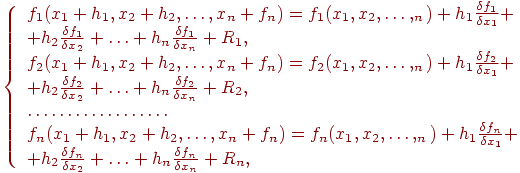
где
hj-
приращение по каждой xj;
Ri
- остаточные нелинейные члены второго
и более высоких порядков каждого ряда
Тейлора. Если приращения hj
таковы, что переменные xj
принимают значения близкие к корню, то
будем считать, что левые части уравнений
системы обращаются в нули. Тогда отбросив
Ri
сведем задачу решения системы нелинейных
уравнений к решению системы линейных
уравнений, в которой неизвестными
являются приращения hj,
.
(7)
Это
система линейных уравнений с неизвестными
hj
,
.
Запишем ее в матричной форме
где :
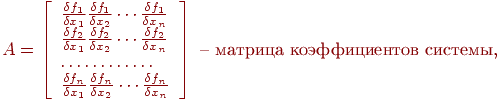
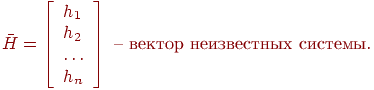
Матрица А, составленная из частных производных называется матрицей Якоби, а её определитель - Якобианом.
Ну
и блок – схема:
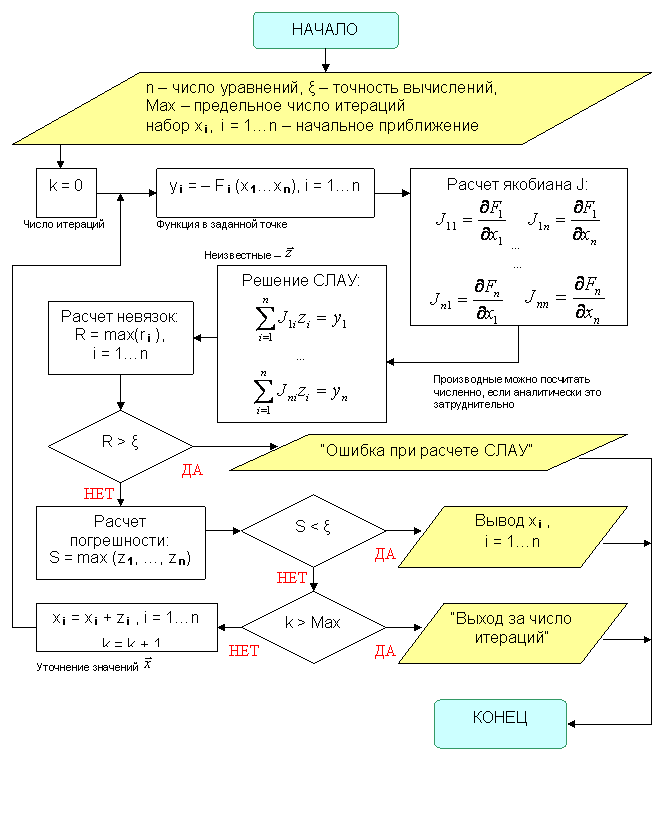
Возможности matlab для решения систем нелинейных уравнений.
Решение нелинейных уравнений и систем выполняется с помощью функции fsolve.
>> fsolve(< имя функции>, <начальное значение>,<опции>),
Где < имя функции> - имя М-функции, которая определяет левую часть уравнения f(x)=0 или системы уравнений F(x)=0: она должна принимать на входе вектор аргументов и возвращать вектор значений; <начальное значение> - вектор приближений, относительно которого будет осуществляться поиск решения.
Где <опции> - дополнительные параметры управления вычислительным процессом. Их можно определить с помощью функции
optimset (<вид контроля>, <значение>).
---------------------------------------------------------------------------------------------------------------------
ВОПРОС №19
Интерполирование функций каноническими полиномами, оценка погрешности. Реализация интерполяции в MATLAB.
---------------------------------------------------------------------------------------------------------------------