
Логит-модели
а) метод оценки коэффициентов;
Оценивается методом максимального правдоподобия (ММП) не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является наилучшим.
Оценки максимального правдоподобия при больших n, состятельны и асимптотически нормальны и асимптотически эффективны.
Альтернативный
подход к построению аналога коэффициента
для моделей бинарного выбора.

Поскольку для оценивания таких моделей используется метод максимального правдоподобия, то естественным представляется сравнение максимумов функций правдоподобия (или максимумов логарифмических функций правдоподобия) для выбранной и тривиальной моделей.
Пусть
– максимум функции правдоподобия для выбранной модели, а L1
– максимум функции правдоподобия для тривиальной модели L0
При этом L0 ≤ L1 ≤ 1 так что и lnL0 ≤lnL1 ≤ 0
б) формальная запись модели
F(z)=
в) показатели качества модели
Pseudo = 1-
McFadden
=1-
– максимум функции правдоподобия для выбранной модели, а L1
– максимум функции правдоподобия для тривиальной модели L0
При этом L0 ≤ L1 ≤ 1 так что и lnL0 ≤lnL1 ≤ 0
Модели множественного выбора:
а) метод оценки коэффициентов;
Функции не линейны по параметрам и оцениваются ММП.
ММП не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является наилучшим.
Оценки максимального правдоподобия при больших , состятельны и асимптотически нормальны и асимптотически эффективны.
б) формальная запись модели
Логит- и пробит-модели множественного выбора представляют собой обобщение моделей бинарного выбора.
Предполагается,
что существует некоторая количественная
латентная
(скрытая) переменная
zt,
связанная с факторами
![]()
Yt=1, когда zt превосходит некоторое пороговое значение (например 0)
Yt=0, когда меньше порогового значения
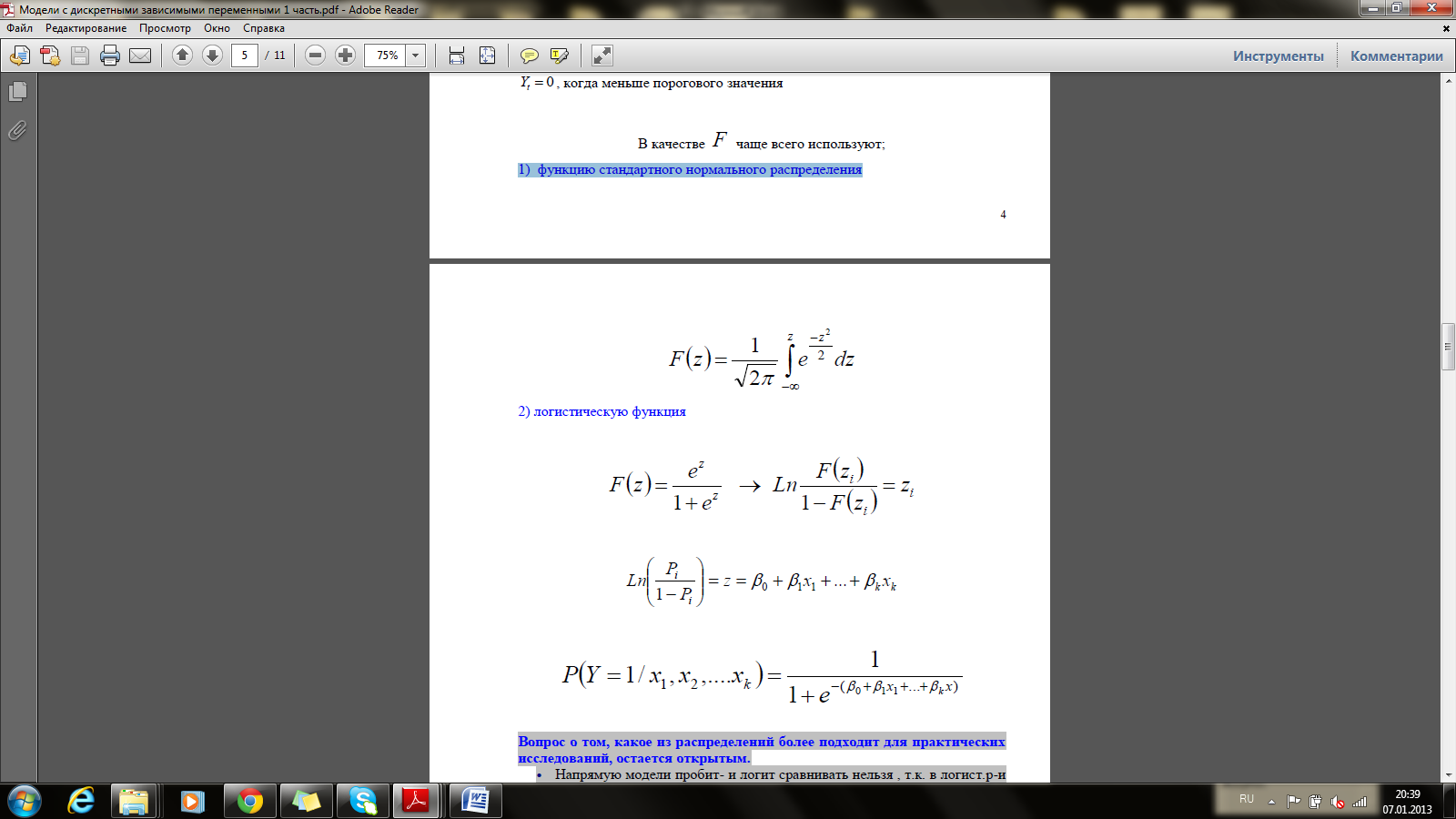
В качестве F чаще всего используют;
1) функцию стандартного нормального распределения
2) логистическую функцию
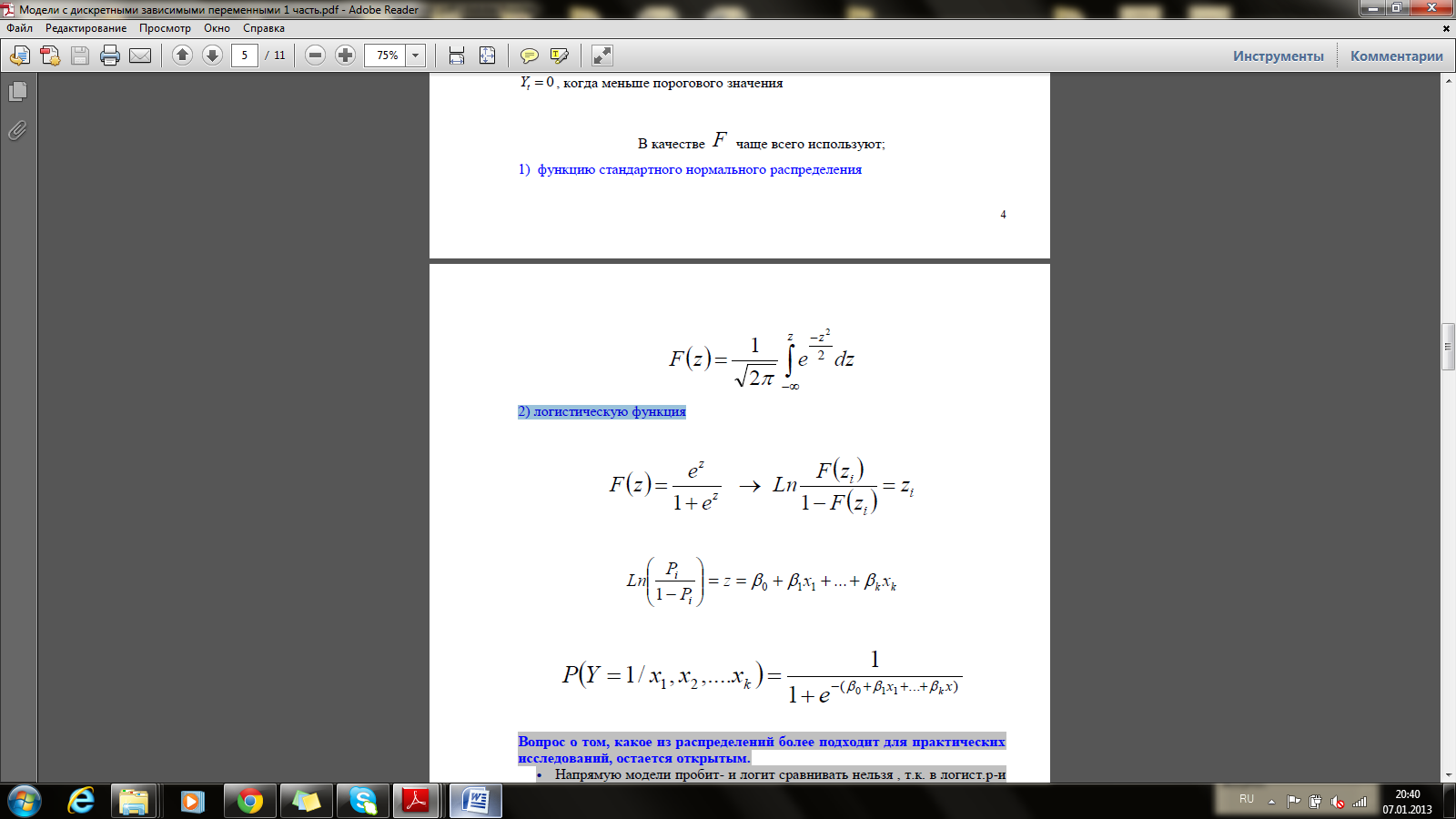
Вопрос о том, какое из распределений более подходит для практических исследований, остается открытым.
Практика показывает, что при отсутствии существенного преобладания одной альтернативы над другой, а также для выборок с небольшим разбросом переменных, выводы, полученные на основе probit- и logit- моделей, как правило, совпадают.
в) показатели качества модели
1.Для упорядоченных альтернатив-дискретная зависимая переменная является порядковой, то есть альтернативы естественным образом упорядочены.
Модели основываются на введении латентной переменной u, изменяющейся от минус бесконечности до плюс бесконечности и порождающей зависимую переменную y.
Качество модели и значимость коэффициентов оцениваются ММП
2.Для неупорядоченных альтернатив-каждая альтернатива имеет случайный уровень полезности и выбирается альтернатива, приносящая наибольшую полезность. такие модели – модели случайной полезности.
Качество модели можно оценить, рассчитав процент верных прогнозов.
Для проверки значимости модели в целом используется тест отношения правдоподобия LR.
