2. Эконометрическая модель, основные этапы построения эконометрической модели. Основное отличие эконометрических моделей от других видов моделей заключается в обязательном включении в модель случайной ошибки. Случайная ошибка характеризуется следующими свойствами:

1) математическое ожидание случайной ошибки при всех значениях эндогенной переменной равно нулю;

2) дисперсии случайной ошибки удовлетворяют свойству гомоскедастичности, т. е. постоянства дисперсий.

Отличительные особенности э.м.:

-учитывает вероятностный характер

-носит конкретный характер

-включает влияние случайных факторов Пример эконометр. Модели: y_i=a-bx_i+ε_i– пример эконометрической модели

1-й этап (постановочный) - определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли;2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез; 3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными; 4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей; 5-й этап (идентификация модели) – статистич. анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели (корректную процедуру оценивания неизвестных параметров модели по имеющимся исходным данным);6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.

3. Парная линейная регрессия.

Классические предположения модели. Классическая модель множественной регрессии.

Как известно, явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, то есть эти явления многофакторны. Между факторами существуют слож­ные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить меру влияния на исследуемый результатив-ный показатель каждого из включенных в модель (уравнение) факто­ров при фиксированном положении (на среднем уровне) ос­тальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретиче­ское значение этого показателя. Важным условием является от­сутствие между факторами функциональной или сильно корреляционной связи.

Математически задача формулируется следующим образом. Требуется найти аналитическое выражение, наилучшим образом отражающее установленную теоретическим анализом связь не­зависимых признаков с результативным, то есть функцию вида:

y_i=f(х₁, х₂, …, х_n) + ε_i (1)

Данное выражение является классической нормальной моделью множественной регрессии.

Применяя ЭВМ, выбор аппроксимирующей математической функции осуществляется перебором решений, наиболее часто используемых в анализе и решении корреляционно-регрессионных уравнений.

После выбора типа аппроксимирующей функции приступают к многофакторному корреляционному и регрессионному анализу, задачей которого является построение уравнения множественной регрессии и нахождение его неизвестных параметров а₀, а₁, а₂, …, а_n.

Параметры уравнения множественной регрессии, как и в случае парной регрессии, находят по способу наименьших квадратов. Затем с помощью корреляционного анализа осуществляют про­верку адекватности полученной модели. Адекватную модель эко­номически интерпретируют.

Частным случаем выражения (1) является уравнение множест­венной линейной двухфакторной регрессии вида

ŷ_х1…хi = a₀ + a₁·х₁ + a₂·x₂ (2)

где ŷ_х1…хi– расчетные значения зависимой переменной (результа­тивного признака); х₁, x₂ – независимые переменные (факторные признаки); а₀, а₁и а₂ – параметры уравнения.

Для расчета параметров уравнения (2) применяется следующая система линейных уравнений:

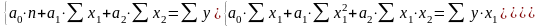(3)

Для решения уравнения множественной регрессии с n-факторами

ŷ_х1…хi = a₀ + a₁·х₁ + a₂·x₂ + …+ a_n·x_n (4)

применяется следующая система нормальных уравнений:

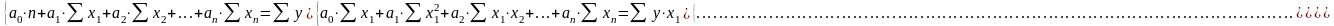(5)

Вручную целесообразно выполнять построение и анализ только двух-, максимум трехфакторных моделей. Для n>3 все расчеты рекомендуется осуществлять на компьютерах по специальным программам, предусматривающим исчисление параметров уравнения и показателей, используемых для проверки его адекватности.

• МНК (система нормальных уравнений, формулы для расчета коэффициентов).

Наименьших квадратов метод – решение, для которого минимизируется сумма квадратов отклонений между наблюдаемыми и предполагаемыми значениями; в факторном анализе – метод получения первоначального факторного решения.

• Свойства оценок.

Каждая случайная величина полностью определяется своей функцией распределения.При решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Аналогичные формулы справедливы для функций дискретной случайной величины:

, 

Основные свойства математического ожидания:

математическое ожидание константы равно этой константе, Mc=c ;

математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )².Легко показать, что Dx = M(x - Mx )²= Mx ² - M(x )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

Основные свойства дисперсии:

дисперсия любой случайной величины неотрицательна, Dx   0;

дисперсия константы равна нулю, Dc=0;

для произвольной константы D(cx ) = c²D(x );

дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ±h ) = D(x ) + D (h ).

• Проверка качества парной линейной регрессии:

- значимость параметров t-тест: а) тестируемая гипотеза, б) формула для расчета критической статистики; В линейной регрессии оценивается так4же значимость параметров. С этой целью по каждому из параметров вычисляется стандартная ошибка.

S- остаточная сумма квадратов на одну степень свободы или остаточная дисперсия. Величина стандартной ошибки совместна с t- распределением стьюдента, поэтому для оценки существенности параметра b его величина сравнивается со стандартной ошибкой и вычисляется значение  и оно сравнивается см табличным значением t критерия. Выводы такие же как при использовании f критерия. Доверительный интервал для коэффициента регрессии в этом случае определяется следующим образом  стандартная ошибка параметра a

Процедура оценивания существенности параметра ф аналогично процедуре оценивания параметра b. Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции. фактическое значение t-критерия стьюдента.

- коэф. детерминации формула и интерпретация Коэффициент детерминации (  - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру связи одной случайной величины от множества других.

- F-тест: а) тестируемая гипотеза, б) формула для расчета критической статистики;

F- статистика (F- statistics) – критерий для проверки существенности уравнения регрессии. Если расчетное значение критерия больше табличного (с уровнем значимости  и степенями свободы 1 и (n – m) ), то можно считать, что уравнение регрессии значимое.

После того, как найдено уравнение регрессии проводится оценка значимости его параметров, а также уравнения в целом. Оценка значимости уравнений проводится с помощью F критерия Фишера. Для этого выдвигается гипотеза Но, которая говорит, что b=0, что при Х не оказывае6т влияние на У.Непосредственно расчету критерия предшествует анализ дисперсии. Центральное место в этом анализе занимает разложение общей суммы квадратов на 2 составляющие: объясненную и необъясненную.

первая сумма-общая сумма квадратов отклонений результативного признака от среднего уровня. Вторая сумма – сумма квадратов отклонений, объясненная регрессией (факторная).третья сумма- остаточная сумма отклонений, необъясненная часть.

3. Множественная линейная регрессия.

• Классические предположения. Теорема Гаусса- Маркова.

Если модель правильно специфицирована, то есть зависимость вида

действительно существует.

- являются детерминированными величинами и не равны все между собой.

При этом:

1. Математическое ожидание регрессионных остатков равно 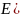0.

)=0

2. Дисперсия остатков постоянна и конечна для всех значений Х, т.е.

)=

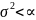
3. Остатки являются статистически независимыми друг от друга, т.е.

)=0

4. Регрессионные остатки и объясняющие переменные независимы друг от друга, т.е.

)=0

5. В случае множественной регрессии – отсутствие мультиколлинеарности.

Тогда МНК оценки ,
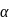