8. Вязкость - внутреннее трение, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой

Уравнение Ньютона: F = (dv/dx)Sη.

Коэффициент вязкости - Коэффициент пропорциональности, зависящий от сорта жидкости или газа. Число, служащее для количественной характеристики свойства вязкости. Коэффициент внутреннего трения.

Неньютоновской жидкостью называют жидкость, при течении которой её вязкость зависит от градиента скорости, течение которых подчиняется уравнению Ньютона. (Полимеры, крахмал, жидкое мыло кровь)

Ньютоновская - Если в движущейся жидкости её вязкость зависит только от её природы и температуры и не зависит от градиента скорости. (Вода и дизельное топливо)

9. Метод Стокса, В основе  метода Стокса лежит формула для силы сопротивления, возникающей при движении шарика в вязкой жидкости, полученная Стоксом:  Fc = 6 π η V r. Чтобы косвенно измерить  коэффициент вязкости  η следует рассмотреть равномерное движение шарика в вязкой жидкости и применить условие равномерного движения: векторная сумма всех сил, действующая на шарик равна  нулю.

. mg + F_A + F_с=0 (всё в векторной форме!!!)

Теперь следует выразить силу тяжести (mg) и силу Архимеда (Fа) через известные величины. Приравнивая величины mg = Fа+Fс   получаем выражение для вязкости:                            

 η = (2/9)*g*(ρ_т - ρ_ж)* r² / v  = (2/9) * g *(ρ_т- ρ_ж)* r²* t / L. Непосредственно измеряются микрометром радиус шарика r (по диаметру), L - путь шарика в жидкости, t- время прохождения пути L. Для измерения вязкости по методу Стокса путь L берется не от поверхности жидкости, а между отметками 1 и 2.  Это вызвано следующим обстоятельством. При выводе рабочей формулы для коэффициента вязкости по методу Стокса использовалось условие равномерного движения. В самом начале движения (начальная скорость шарика равна нулю) сила сопротивления  также равна нулю и шарик имеет некоторое ускорение. По мере набора скорости сила сопротивления увеличивается, равнодействующая трех сил  - уменьшается!  Только после некоторой отметки движение можно считать равномерным  (и то,  - приблизительно).

10. Вискозиметр Освальда представляет своеобразную пипетку с расширением в виде шарика чуть выше тонкого капилляра - левое рабочее колено. В правое вспомогательное колено набирается жидкость (сначала с известной, потом с неизвестной вязкостью). Затем эта жидкость засасывается в шарик, и измеряется время  ее истечения  через капилляр.   Как показывает опыт время истечения одинакового объема различной  жидкости - разное. Это объясняется формулой Пуазейля, записанной для объема протекающей через капилляр жидкости:

 V  = πr ⁴ ΔP*t / 8ηL  - чем больше коэффициент вязкости η, тем больше время истечения  этой жидкости t.

 Для получения рабочей формулы следует заменить в  формуле Пуазейля разность давлений ΔP на гидростатическое давление ρgh (h = L). Тогда получится:

V  = πr⁴ρg t / 8η. Записав эту формулу для двух одинаковых объемов - эталонной и исследуемой жидкости, приравняв правые части каждой формулы и заменив ρ/η=1/v, где v кинематическая вязкость, получили v=v₀t/t₀ , где v₀ и t₀ кинематич.вязкость и время прохождения воды.

11. Формула Пуазёйля: При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.

Гидравлическое сопротивление

Х = 8ηl / (πR⁴)

12. Последовательное соединение.

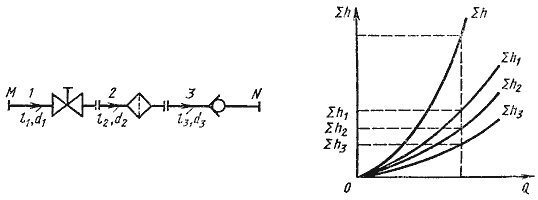
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:Q₁ = Q₂ = Q₃ = Q Σ^h_M-N ⁼ Σ^h₁ ⁺ Σ^h₂ ⁺ Σ^h₃

Параллельное соединение

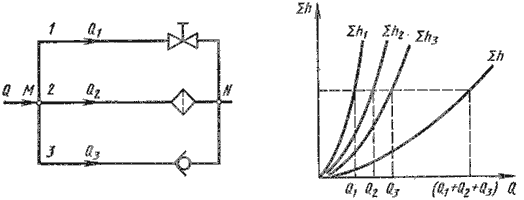
Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.Очевидно, что расход жидкости в основной магистрали

Q = Q1 = Q2 = Q3, Σh1 = HM - HN; Σh2 = HM - HN;Σh3 = HM – HN, Σh1 = Σh2 = Σh3

т.е. потери напора в параллельных трубопроводах равны между собой

13. Пов натяжение жидкости заключается в стремлении вещества уменьшить избыток своей потенциальной энергии на границе раздела с др фазой (пов энергию). На пов-тях раздела жид-ти и ее насыщ пара, двух несмешиваемых жид-й, жид-ти и тв тела возникает сила, обусловленная различным межмолекулярным взщаимодействием граничащих сред.Силы пов натяжения направлены по касательной к поверхности жидкости, перпендикулярно к участку контура на котор они действуют и пропорциональныдлине этого участка.

Коэф-т пов натяжения α=F/l=A/S

Капиллярность-физ явление, заключающееся в способности жидкостей изменять уровень в

трубках, узких каналах произвольной формы, пористых телах. Поднятие – в случае смачивания.

14. Закон Гука - связь между величиной упругой деформации и силой, действующей на тело. F= -K X

-1- величина абсолютной деформации пропорциональна величине деформирующей силы с коэффициентом пропорциональности равным жесткости деформируемого образца;  -2- сила упругости, возникающая в деформированном теле, пропорциональна величине деформации с коэффициентом пропорциональности равным жесткости деформируемого образца;  -3- упругое напряжение, возникающее в теле, пропорционально относительной деформации этого тела с коэффициентом пропорциональности равным модулю упругости.

М одуль упругости - коэффициент, характеризующий сопротивление материала к растяж. Сжат.

ОА-упр деф.В предел упругости СД предел текучести.Д предел прочности.

15.Закон Ома для переменного тока

Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

U = U0eiωt — напряжение или разность потенциалов,

I — сила тока,

Z = Re−iδ — комплексное сопротивление (импеданс),

R = (Ra2 + Rr2)1/2 — полное сопротивление,

Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),

Rа — активное (омическое) сопротивление, не зависящее от частоты,

δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.

Реактивное сопротивление – это сопротивление катушек индуктивности (дросселей) и конденсаторов. Величина реактивного сопротивления уже зависит от частоты тока. Так на постоянном токе реактивное сопротивление конденсатора устремляется к бесконечности, а дросселя наоборот – к нулю (без учета активной составляющей сопротивления провода).

С изменением частоты тока электрическое сопротивление конденсатора изменяется, по закону:

Xc = 1/2pfC2

где Xc – сопротивление, Ом; f – частота, Гц; С – емкость, Ф.

Электрическое сопротивление конденсатора переменному току можно измерить. Зная сопротивление и частоту тока, легко по формуле вычислить емкость. Кроме того, если в электрической цепи стоит конденсатор происходит сдвиг фаз напряжения и тока. Причем ток опережает напряжение на величину 90°.

Реактивное сопротивление катушки индуктивности с увеличением частоты возрастает:

XL = 2pfL

где XL – сопротивление катушки, Ом; f – частота, Гц; L – индуктивность, Гн.

Индуктивность дросселя легко вычисляется по известному сопротивлению и заданной частоте тока. При этом фазы напряжения и тока на катушке индуктивности сдвигаются относительно друг друга, и теперь ток отстает от напряжения на 90°.

Для измерения реактивного сопротивления емкости и индуктивности потребуется, прежде всего, переменный ток синусоидальной формы. С задачей программного генератора с легкостью может справиться звуковая плата компьютера. Другая проблема – определение величины электрического сопротивления измеряемого элемента. Но оказывается и эту задачу можно решить программным путем, с помощью той же звуковой платы, не прибегая к специальным аналого-цифровым преобразователям