1 Способ:

. В условиях задачи

P(4,5<

2 Способ:

По формуле:

_, a=4,5; b=7

Тогда:

г) Математическое ожидание и дисперсия

Математическое ожидание находим по формуле:

М

Дисперсию вычисляем по формуле:

д )Строим графики и :

Тренинг умений: [2] №№262,267,275,280,295.

Задача 2.3

Случайные величины имеют геометрическое, биноминальное и пуассоновское распределения соответственно. Найти вероятности , если математические ожидания , а дисперсия .

Решение:

1. Случайная величина имеет геометрическое распределение, если её возможные значения 1,2,3,4…. , а вероятности этих значений .

Известно, что ; тогда ; так как , тогда

Вычислим:

2. Случайная величина имеет биноминальное распределение, если она принимает значения 0,1,2,3… с вероятностями:

Известно, что:

тогда, решая эту систему получим:

Вычислим:

=

3. Случайная величина имеет распределение Пуассона, если ее возможные значения 0,1,2…, а соответствующие вероятности вычисляются по формуле:

, где

Тогда:

Задача 2.4

Случайные величины имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности , если у этих случайных величин математические ожидания и среднее квадратические отклонения равны 3.

Решение:

,

Надо найти

1. Для равномерно распределенной на отрезке [a,b] случайной величины функция плотности имеет вид.

Математическое ожидание вычисляется по формуле:

Дисперсия:

Отсюда, среднее квадратическое отклонение (

По условию задачи имеем:

При эта система равносильна системе:

,

решая которую, получаем:

Отсюда: .

Значит, функция плотности имеет вид:

Найдем вероятность по формуле попадания значений случайной величины с функцией плотности в :

2. Непрерывная случайная величина имеет показательное распределение, если ее плотность вероятности:

где параметр распределения,

Функция распределения показательного распределения имеет вид:

Известно, что , отсюда

Тогда:

Вычислим :

3. Пусть случайная величина, подчиняющаяся нормальному закону распределения. Основные параметры случайной величины имеющей нормальный закон распределения X : математическое ожидание, среднее квадратическое отклонение. По условию задачи , .Так как вероятность попадания случайной величины в распределенной по нормальному закону, вычисляется по формуле

где Ф(x) – функция Лапласа (значения ее берутся из таблицы), то по условию задачи:

Тренинг умений: [2] №№315,328,350,367.

Математическая статистика.

Тема 3: численная обработка данных одномерной выборки.

Выборка X объемом N = 100 измерений получится в виде таблицы

где рассчитаны по формуле:

,

Объем выборки -

Примечание.Для расчетов и рекомендуется перейти к условным значениям , взяв за ложный нуль С_х значение с наибольшей частотой, использовать суммы и .

Задача 3.1

Построить полигон относительных частот .

Решение:

Для построения полигона вычислим по формуле относительные частоты:

Контроль:

(полигон получен соединением отрезками ломаной точек с координатами:( , )) .

Задача 3.2

Вычислим среднее выборочное , выборочную дисперсию и среднее квадратическое отклонение .

Решение:

Возьмём за ложный нуль и перейдем к условным вариантам (выбрано с наибольшей частотой )

(в знаменателе )

Распределение условных вариант (значений):

Вычислим:

По формуле ,

получим средняя выборочная

Вычислим:

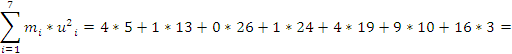
По формуле:

вычислим:

выборочная дисперсия.Так как , то ,

значит среднее квадратическое отклонение.

Задача 3.3

По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости

Решение:

Численным методом оценки того, принадлежит ли данная выборка генеральной совокупности с нормальным законом распределения с параметрами М(Х)= , является метод применения критерия (критерий К. Пирсона – один из критериев согласия). По этому методу наблюдаемое эмпирическое распределение выборки сравнивается с гипотетическим теоретическим распределением соответствующей генеральной совокупности. Для этого необходимо:

1. Вычислить , где N – объем выборки, - шаг (разность между двумя соседними измерениями), , – табличное значение функции Гаусса.

Составим расчетную таблицу 1. Значения получены из таблицы значений функции Гаусса ;

Таблица 1.

2. Сравнить эмпирические и теоретические частоты с помощью критерия. Составим расчетную таблицу 2, из которой найдем наблюдаемые значения критерия

Таблица 2.

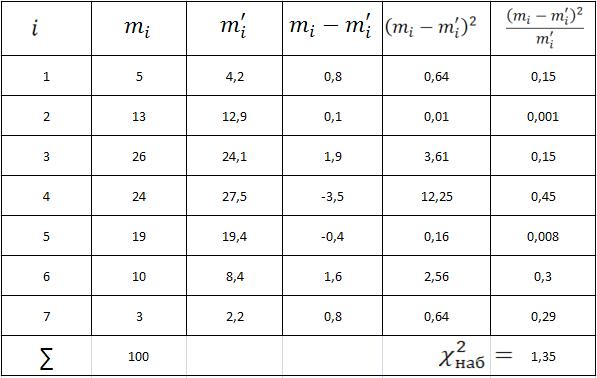
3. По таблице критических точек распределения по уровню значимости и числу степеней свободы найдем критическую точку правосторонней критической области . Так как нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, то есть эмпирические и теоретические частоты различаются незначимо (случайно).

Тренинг умений: [2] №№443,446,453,466,501,506,510,635

ІV. Задания к контрольной работе