3.2 Машинные эксперименты с разработанными программами
Непосредственные результаты работы программы с исходными данными на курсовую работу можно увидеть на рисунке 3.1.
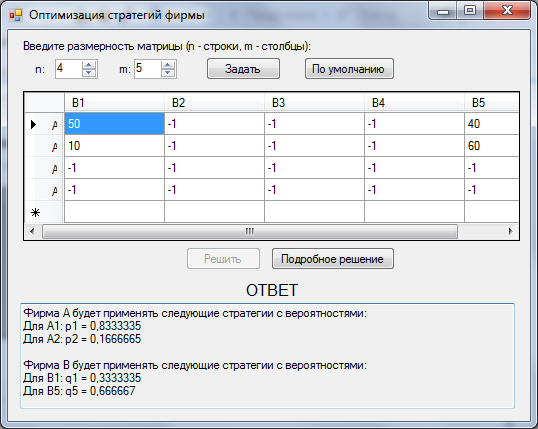
Рисунок 3.1- Результаты работы программы
Точность результатов можно увеличить, задав в программе большее значение переменной z, отвечающей за точность округления. В примере, изображенном выше, z=8, т.е. округление происходит до 8 цифры после запятой.
3.3 Сравнение результатов ручного и машинного расчетов
В результате ручных расчетов получены вероятности применения стратегий фирмами.
Фирма А будет использовать следующие стратегии:
А1 с вероятностью 0,8333;
А2 с вероятностью 0,1667.
Стратегии А3 и А4 использоваться не будут.
Фирма В будет использовать следующие стратегии:
В1 с вероятностью 0,3333;
В5 с вероятностью 0,6667.
Стратегии В2, В3 и В4 использоваться не будут.
Вычислительные эксперименты с отлаженной программой дали аналогичные результаты. Кроме того, все промежуточные расчёты, производимые при ручной реализации алгоритма, полностью соответствуют таковым в программе.
Заключение
В ходе выполнения курсовой работы были получены и закреплены навыки в решении задач теории игр. Также было разработан программный продукт для решения задачи об оптимизации стратегий фирм.
Он позволяет пользователю самому ввести данные для решения необходимой ему задачи (но для наглядности в памяти приложения сохранен контрольный пример) и получить её решение в краткой или подробной форме с описанием каждого шага решения.
Применение данного программного продукта на практике позволит оптимизировать выбор стратегий реализации товаров фирмами .
Список литературы
Черноморов Г.А. Теория принятия решений: Учебное пособие / Юж.-Рос. гос. техн. ун-т Новочеркасск: Ред. журн. “Изв. вузов Электромеханика”, 2002, 276с.
Wikipedia [Электронный ресурс]. 2013. URL: http://ru.wikipedia.org (Дата обращения: 5.12.2013).
Джо Майо. Microsoft Visual Studio 2010. Самоучитель. Изд.БХВ-Петербург 2010 г.
Приложение а Листинг программы
Содержание файла DetailSolutionForm.cs:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace TPR_Kurs
{
public partial class DetailSolutionForm : Form
{
public DetailSolutionForm(int n, int m)
{
InitializeComponent();
for (int i = 0; i < n; i++)
{
sourceGrd.Columns.Add("", "B" + (i + 1));
sourceSimpleGrd.Columns.Add("", "B" + (i + 1));
simpleGrd.Columns.Add("", "B" + (i + 1));
}
for (int j = 0; j < m; j++)
{
sourceGrd.Rows.Add();
sourceGrd.Rows[j].HeaderCell.Value = "A" + (j + 1);
sourceSimpleGrd.Rows.Add();
sourceSimpleGrd.Rows[j].HeaderCell.Value = "A" + (j + 1);
simpleGrd.Rows.Add();
simpleGrd.Rows[j].HeaderCell.Value = "A" + (j + 1);
}
for (int j = 0; j < n; j++)
for (int i = 0; i < m; i++)
{ sourceGrd[j, i].Value = Data.sourceA[i, j];
sourceSimpleGrd[j, i].Value = Data.a1[i, j];
simpleGrd[j, i].Value = Data.a2[i, j];
}
textBox1.Text = Data.solText;
textBox2.Text = Data.answer;
}
}
}
Содержание файла MainForm.cs:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace TPR_Kurs
{
public partial class MainForm : Form
{
int z = 8; // точность округления
public MainForm()
{
InitializeComponent();
// матрица по умолчанию
int[,] a = new int[4,5] { { 50, 80, 70, 50, 40 }, {10,10,50,50,60 }, {20,40,30,60,20 }, {30,50,40,40,30 } };
for (int i = 0; i < 5; i++) exampleGrd.Columns.Add("", "B" + (i + 1));
for (int j = 0; j < 4; j++) { exampleGrd.Rows.Add();
exampleGrd.Rows[j].HeaderCell.Value = "A" + (j + 1); }
for (int j = 0; j < 5; j++)
for (int i = 0; i < 4; i++)
exampleGrd[j, i].Value = a[i, j];
}
// // Обработка нажатия кнопки "Задать"
private void razmerBtn_Click(object sender, EventArgs e)
{
Data.solText = " ";
textBox1.Clear();
textBox2.Clear();
exampleGrd.AutoResizeColumns();
exampleGrd.Columns.Clear();
int n = int.Parse(ntxt.Text);
int m = int.Parse(mtxt.Text);
for (int i = 0; i < m; i++)
{
exampleGrd.Columns.Add("", "B"+(i+1));
}
for (int j = 0; j < n; j++)
{
exampleGrd.Rows.Add();
exampleGrd.Rows[j].HeaderCell.Value = "A"+(j+1);
}
detailSolBtn.Enabled = false;
solutionBtn.Enabled = true;
}
// Обработка нажатия кнопки "Решить"
private void solutionBtn_Click(object sender, EventArgs e)
{
int i = 0, j = 0;
// размер исходной матрицы
int n = exampleGrd.ColumnCount; // столбцы
int m = exampleGrd.RowCount - 1; // строки
Data.n = n;
Data.m = m;
float[,] a = new float[m, n]; // матрица
float[,] sourceA = new float[m, n];
//------------------------------------------------------------------------------
//--------------------------- ШАГ 1 ------------------------------------
//------------------------------------------------------------------------------
textBox1.Text += "\tШАГ 1:\r\nРазмерность: n=" + n + " m=" + m + "\r\nИсходная матрица:\r\n";
for (j = 0; j < m; j++)
{
for (i = 0; i < n; i++)
{
a[j, i] = Convert.ToInt32(exampleGrd[i, j].Value);
sourceA[j, i] = a[j, i];
textBox1.Text += a[j, i].ToString() + " ";
}
textBox1.Text += " \r\n";
}
Data.sourceA = sourceA; Data.a = Data.a1=Data.sourceA;
solution(a, Data.n, Data.m);
}
// Функция основного алгоритма программы
public void solution( float[,] a, int n, int m)
{
int i = 0, j = 0, k = 0, optA = 0, optB = 0;
float alpha = 0, beta = 0, min = 0;
float[,] sourceSimpleA = new float[m, n];
float[] Bn = new float[n]; // оптиммальные стратегии для B
float[] Am = new float[m]; // оптиммальные стратегии для А
// вычисление минимальных элементов строк
textBox1.Text += "\r\nМинимальные элементы строк: ";
for (i = 0; i < m; i++)
{
Am[i] = a[i, 0];
for (j = 1; j < n; j++)
if (a[i, j] < Am[i])
Am[i] = a[i, j];
textBox1.Text += Am[i] + " ";
}
alpha = Am[0]; optA = 1;
for (i = 1; i < m; i++)
{
if (Am[i] > alpha)
{ alpha = Am[i]; optA = i + 1; }
}
textBox1.Text += "\r\nalpha=" + alpha;
// вычисление максимальных элементов слобцов
textBox1.Text += "\r\nМаксимальные элементы стролбцов: ";
for (j = 0; j < n; j++)
{
Bn[j] = a[0, j];
for (i = 1; i < m; i++)
{
if (a[i, j] > Bn[j])
Bn[j] = a[i, j];
}
textBox1.Text += Bn[j] + " ";
}
beta = Bn[0]; optB = 1;
for (i = 1; i < n; i++)
{
if (Bn[i] < beta)
{ beta = Bn[i]; optB = i + 1; }
}
textBox1.Text += "\r\nbeta=" + beta;
if (alpha == beta)
textBox1.Text += "\r\nИгра имеет седловую точку. Игра решается в чистых стратегиях. " +
"Оптимальная стратегия для фирмы А: A" + optA + ", а для В - B" + optB;
else // решение в смешанных стратегиях
{
textBox1.Text += "\r\nИгра не имеет седловой точки. Игра решается в смешанных стратегиях. Переходим ко 2 шагу.\r\n";
//-----------------------------------------------------------------------
//--------------------------- ШАГ 2 ------------------------------
//-----------------------------------------------------------------------
// поиск минимального элемента массива
textBox1.Text += "\r\n\tШАГ 2";
min = a[0, 0];
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
if (min > a[i, j])
min = a[i, j];
min = (float)Math.Round(min, z);
textBox1.Text += "\r\nМинимальный элемент матрицы " + min.ToString();
if (min < 0)
{
textBox1.Text += "\r\nМинимальный элемент матрицы отрицательный. Необходимо преобразовать матрицу, добавив к каждому её элементу значение минималльного элемента.\r\n";
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
{
a[i, j] += Math.Abs(min);
sourceSimpleA[i, j] = a[i, j];
exampleGrd[j, i].Value = a[i, j];
}
Data.a1 = a;
}
else
textBox1.Text += "\r\nМинимальный элемент матрицы положительный.Матрица не требует преобразований.\r\n";
// Объявление переменных для упрощения матрицы
int[] Astr, Bstr, Acount, Bcount; // Astr и Bstr массивы с доминирующими стратегиями. Сначала все 1.
// Acount и Bcount - промежуточные переменные для опреления доминирующих стратегий
bool Aflag = false, Bflag = false; // Флаги для цикла - если в ходе итерации не удалили ни одной строки или столбца - выйти из цикла
Astr = new int[m]; Bstr = new int[n]; Acount = new int[m]; Bcount = new int[n];
for (i = 0; i < m; i++)
{
Astr[i] = 1; Acount[i] = 0;
}
for (i = 0; i < n; i++)
{
Bstr[i] = 1; Bcount[i] = 0;
}
// Упрощение матрицы
textBox1.Text += "\r\n\tУпрощение матрицы";
while (Aflag == false || Bflag == false)
{
Aflag = true; Bflag = true;
for (i = 0; i < m; i++)
{
if (Astr[i] == 1)
{
for (j = 0; j < n; j++)
{
for (k = 0; k < m; k++)
if ((i != k) & (a[i, j] < a[k, j])) Acount[k]++;
}
// Удаление строк - в нашем случае заполнение их значением -1
for (k = 0; k < m; k++)
if ((k != i) & (Acount[k] == 0) & (Astr[k] == 1))
{
textBox1.Text += "\r\nСтратегия А" + (i + 1) + " доминирует над стратегией А" + (k + 1) + ". Удаляем А" + (k + 1) + ".";
Astr[k] = 0;
Aflag = false;
for (j = 0; j < n; j++)
{
a[k, j] = -1;
exampleGrd[j, k].Value = a[k, j];
}
}
for (k = 0; k < m; k++) Acount[k] = 0;
}
}
// удаление столбцов
for (i = 0; i < n; i++)
{
if (Bstr[i] == 1)
{
for (j = 0; j < m; j++)
{
for (k = 0; k < n; k++)
if ((i != k) & (a[j, i] > a[j, k])) Bcount[k]++;
}
// Удаление столбцов - в нашем случае заполнение их значением -1
for (k = 0; k < n; k++)
if ((k != i) & (Bcount[k] == 0) & (Bstr[k] == 1))
{
textBox1.Text += "\r\nСтратегия B" + (i + 1) + " доминирует над стратегией B" + (k + 1) + ". Удаляем B" + (k + 1) + ".";
Bstr[k] = 0;
Bflag = false;
for (j = 0; j < m; j++)
{
a[j, k] = -1;
exampleGrd[k, j].Value = a[j, k];
}
}
for (k = 0; k < n; k++) Bcount[k] = 0;
}
}
} // Конец while
Data.a2 = a;
int x = 0, y = 0; // Размерность упрощенной матрицы: x - строки, y - столбцы
int d = 0;
for (j = 0; j < m; j++)
if (Astr[j] == 1) x++;
for (i = 0; i < n; i++)
if (Bstr[i] == 1) y++;
// Упрощенная матрица
float[,] aSimple = new float[x, y]; // для А
float[,] bSimple = new float[y, x]; // для В
int[] AOptStr = new int[x];
int[] BOptStr = new int[y];
textBox1.Text += "\r\nОставшиеся стратегии фирм\r\n";
for (j = 0; j < m; j++)
if (Astr[j] == 1) { AOptStr[d] = j; d++; textBox1.Text += "А" + (j + 1) + " ,"; }
d = 0;
for (i = 0; i < n; i++)
if (Bstr[i] == 1) { BOptStr[d] = i; d++; textBox1.Text += "B" + (i + 1) + " ,"; }
// Заполнение упрощенной матрицы А
textBox1.Text += "\r\nУпрощенная матрица:\r\n";
for (i = 0; i < x; i++)
{
for (j = 0; j < y; j++)
{
aSimple[i, j] = a[AOptStr[i], BOptStr[j]];
textBox1.Text += aSimple[i, j] + " ";
}
textBox1.Text += "\r\n";
}
// Заполнение упрощенной матрицы B
textBox1.Text += "\r\n";
for (i = 0; i < x; i++)
for (j = 0; j < y; j++)
bSimple[j, i] = aSimple[i, j];
//-----------------------------------------------------------------------
//--------------------------- ШАГ 3, 4 и 5 ------------------------
//-----------------------------------------------------------------------
textBox1.Text += "\t ШАГ 3, 4:\r\nРешение двойственной задачи линейного программирования.\r\n";
int s = y, p = x;
float[] b1 = new float[p]; // для А
float[] answerA = new float[p];
float[,] temp1 = new float[p, s + 1]; // для А
float[,] answerB = new float[1,s];
float[] b2 = new float[s]; // для В
float[,] temp2 = new float[s, p + 1]; // для В
// для А
for (j = 0; j < p; j++)
for (i = 0; i < s; i++)
temp1[j, i] = aSimple[j, i];
for (j = 0; j < p; j++)
{
temp1[j, s] = 1;
b1[j] = 1;
}
// для В
for (j = 0; j < s; j++)
for (i = 0; i < p; i++)
temp2[j, i] = bSimple[j, i];
for (j = 0; j < s; j++)
{
temp2[j, p] = 1;
b2[j] = 1;
}
simplexMethod(bSimple, aSimple, p,s,ref answerA, ref answerB);
textBox1.Text += "\r\nРешение двойственной задачи ЛП:";
for (i = 0; i < p; i++)
{
answerA[i] = (float)Math.Round(answerA[i], z);
textBox1.Text += "\r\nx" + (i + 1) + " = " + answerA[i];
}
for (i = 0; i < s; i++)
{
answerB[0,i] = (float)Math.Round(answerB[0,i], z);
textBox1.Text += "\r\ny" + (i + 1) + " = " + answerB[0,i];
}
textBox1.Text += "\t ШАГ 5:\r\n Определение цены игры и вероятности применения стратегий фирм \r\n";
// Определим цену игры
float nu1 = 0, znamNu = 0;
for (i = 0; i < p; i++)
znamNu += answerA[i];
nu1 = 1 / znamNu;
nu1 = (float)Math.Round(nu1, z);
textBox1.Text += "\r\nЦена игры Y1 = " + nu1;
// Определим вероятности применения стратегий фирмой А
float[] pStr = new float[p];
textBox1.Text += "\r\nВероятности применения стратегий фирмой А:\r\n";
textBox2.Text += "Фирма А будет применять следующие стратегии с вероятностями:\r\n";
for (i = 0; i < p; i++)
{
pStr[i] = nu1 * answerA[i];
pStr[i] = (float)Math.Round(pStr[i], z);
textBox1.Text += "Для A" + (AOptStr[i] + 1) + ": p" + (AOptStr[i] + 1) + " = " + pStr[i] + "\r\n";
textBox2.Text += "Для A" + (AOptStr[i] + 1) + ": p" + (AOptStr[i] + 1) + " = " + pStr[i] + "\r\n";
}
// Определим вероятности применения стратегий фирмой В
float[] qStr = new float[s];
textBox1.Text += "\r\nВероятности применения стратегий фирмой B:\r\n";
textBox2.Text += "\r\nФирма В будет применять следующие стратегии с вероятностями:\r\n";
for (i = 0; i < s; i++)
{
qStr[i] = nu1 * answerB[0,i];
qStr[i] = (float)Math.Round(qStr[i], z);
textBox1.Text += "Для В" + (BOptStr[i] + 1) + ": q" + (BOptStr[i] + 1) + " = " + qStr[i] + "\r\n";
textBox2.Text += "Для В" + (BOptStr[i] + 1) + ": q" + (BOptStr[i] + 1) + " = " + qStr[i] + "\r\n";
}
// Определим истинную цену игры
float nu;
if (min < 0)
nu = nu1 - Math.Abs(min);
else nu = nu1;
textBox1.Text += "\r\nИстинная цена игры Y = " + nu;
//}
detailSolBtn.Enabled = true;
solutionBtn.Enabled = false;
}
Data.solText = textBox1.Text;
Data.answer = textBox2.Text;
}
//_________Функция расчёта определителя_______
public float detMatr(float[,] b, int n)
{
float x,s;
int i,j,k;
for (i=0; i<n-1; i++)
for (k=i+1; k<n; k++)
{
x=b[k,i]/b[i,i];
for (j=i; j<n; j++) b[k,j]=b[k,j]-b[i,j]*x;
}
s=1;
for (i=0; i<n; i++) s=s*b[i,i];
return s;
}
// Функция для решения ЗЛП двойственным симплекс-методом
public void simplexMethod(float[,] sourceA, float[,] sourceB, int n, int m, ref float[] AnswerA, ref float[,] AnswerB)
{
bool flagPol = false;
bool flagOpt = false;
bool flagNoSol = false;
int count = 0;
int i = 0, j = 0, k = 0, h = 0, masMinPosCol = 0, masMinPosRow = 0;
float[,] tempA1 = new float[m, n + 1];
float[] bA = new float[m];
//float[] bA = new float[] {-6,8,12};
float[] bB = new float[n];
float[] fA = new float[n + m + 1];
float[] X = new float[n + m];
float[] Y = new float[m];
float valueFA = 0;
float valueFB = 0;
int[] basisA = new int[m];
int[] XnamesA = new int[n + m];
float[,] C = new float[1, m];
// индвидуально и сделано для матричной игры
for (i = 1; i <= n; i++)
fA[i] = -1;
// для А
for (j = 0; j < m; j++)
for (i = 0; i < n; i++)
{
tempA1[j, i] = -sourceA[j, i];
sourceA[j, i] = -sourceA[j, i];
}
for (j = 0; j < m; j++)
{
tempA1[j, n] = 1;
bA[j] = -1; //индвидуально и сделано для матричной игры
basisA[j] = n + j + 1; // заполнение названий базисных переменных
}
// Добавляем базисные переменные
float[,] A = new float[m, n + m];
for (j = 0; j < m; j++)
{
for (i = 0; i < n; i++)
A[j, i] = sourceA[j, i];
A[j, n + j] = 1;
}
// Итоговая первая таблица
int x = m + 1, y = n + m + 1;
float[,] tab = new float[x, y];
float[,] tabTemp = new float[x, y];
for (i = 0; i < x - 1; i++)
{
for (j = 0; j < y - 1; j++)
tab[i, j + 1] = A[i, j];
tab[i, 0] = bA[i];
}
for (i = 0; i < y; i++)
tab[x - 1, i] = fA[i];
textBox1.Text += "\r\nИмеем таблицу\r\n";
for (i = 0; i < x; i++)
{
for (j = 0; j < y; j++)
{
textBox1.Text += tab[i, j] + " ";
}
textBox1.Text += "\r\n";
}
while (!flagPol & !flagNoSol)
{
//Проверка на допустимость
count = 0;
foreach (float el in bA)
if (el >= 0) count++;
if (count != m)
{
// проверка на разрешимость
count = 0;
for (i = 0; i < x - 1; i++)
if (tab[i, 0] < 0)
{
for (j = 1; j < y; j++)
if (tab[i, j] < 0) count++;
if (count == 0)
{
textBox1.Text += "Задача неразрешима";
flagPol = true;
flagNoSol = true;
goto Lable;
}
}
textBox1.Text += "План не допустимый";
// Определение новой свободной переменной
minimum(bA, ref masMinPosRow);
textBox1.Text += "\r\nНаибольший отрицательный элемент в столбце свободных членов = " + bA[masMinPosRow] +
"\r\nВедущей будет " + (masMinPosRow + 1) + " строка, а переменную х" + basisA[masMinPosRow] + " следует вывести из базиса";
for (i = 0; i < y - 1; i++)
X[i] = tab[masMinPosRow, i + 1];
// Определение новой базисной переменной
minimumA(X, fA, ref masMinPosCol);
textBox1.Text += "\r\nМинимальное значение соответствует = " + (masMinPosCol + 1) + " столбцу, т.е. переменную х" + (masMinPosCol + 1) +
" необходимо ввести в базис.\r\nНа пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный " + X[masMinPosCol];
basisA[masMinPosRow] = masMinPosCol + 1;
textBox1.Text += "\r\nСписок базисных переменных";
foreach (int c in basisA) textBox1.Text += c + " ";
// Пересчет симплексной таблицы методом Жордано-Гаусса
for (i = 0; i < y; i++)
tabTemp[masMinPosRow, i] = tab[masMinPosRow, i] / X[masMinPosCol];
for (i = 0; i < x; i++)
for (j = 0; j < y; j++)
if (i != masMinPosRow)
{
tabTemp[i, j] = tab[i, j] - (tab[masMinPosRow, j] * tab[i, masMinPosCol + 1] / tab[masMinPosRow, masMinPosCol + 1]);
}
print(tabTemp, x, y);
// Переопределение полей
for (i = 0; i < x; i++)
for (j = 0; j < y; j++)
tab[i, j] = tabTemp[i, j];
for (i = 0; i < x - 1; i++) bA[i] = tab[i, 0];
for (i = 0; i < y; i++)
fA[i] = tab[x - 1, i];
Lable: ; // сюда попадаем, если задача неразрешима.
}
else
{
textBox1.Text += "План допустимый";
flagPol = true;
flagOpt = true;
}
}
if (flagOpt)
{
while (flagOpt & !flagNoSol)
{
// проверка задачи на оптимальность
count = 0;
for (i = 1; i < y; i++)
if (fA[i] > 0) count++;
if (count != 0)
{
// проверка на ограниченность функции
count = 0;
for (i = 1; i < y; i++)
if (fA[i] > 0)
{
for (j = 0; j < x - 1; j++)
if (tab[i, j] < 0) count++;
if (count == (x - 1))
{
textBox1.Text += "Нет решения";
flagNoSol = true;
goto Label2;
}
}
textBox1.Text += "Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.";
// Определение новой базисной переменной.
maximum(fA, ref masMinPosCol);
textBox1.Text += "\r\nВ качестве ведущего выберем столбец, соответствующий переменной x" + masMinPosCol + ", так как это наибольший коэффициент = " + fA[masMinPosCol];
for (i = 0; i < x - 1; i++)
Y[i] = tab[i, masMinPosCol];
// Определение новой свободной переменной.
minimumA2(bA, Y, ref masMinPosRow);
textBox1.Text += "\r\nВычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее положительное. \r\n "
+ "Оно соответствует " + (masMinPosRow + 1) + " строке. \r\nРазрешающий элемент равен " + Y[masMinPosRow] + " и находится на пересечении ведущего столбца и ведущей строки.";
textBox1.Text += "\r\nФормируем следующую часть симплексной таблицы. \r\nВместо переменной x" + basisA[masMinPosRow] + " в план войдет переменная x" + masMinPosCol;
basisA[masMinPosRow] = masMinPosCol;
textBox1.Text += "\r\nСписок базисных переменных";
foreach (int c in basisA) textBox1.Text += c + " ";
// Пересчет симплексной таблицы методом Жордано-Гаусса
for (i = 0; i < y; i++)
tabTemp[masMinPosRow, i] = tab[masMinPosRow, i] / Y[masMinPosRow];
for (i = 0; i < x; i++)
for (j = 0; j < y; j++)
if (i != masMinPosRow)
{
tabTemp[i, j] = tab[i, j] - (tab[masMinPosRow, j] * tab[i, masMinPosCol] / tab[masMinPosRow, masMinPosCol]);
}
print(tabTemp, x, y);
// Переопределение полей
for (i = 0; i < x; i++)
for (j = 0; j < y; j++)
tab[i, j] = tabTemp[i, j];
for (i = 0; i < x - 1; i++) bA[i] = tab[i, 0];
for (i = 0; i < y; i++)
fA[i] = tab[x - 1, i];
}
else
{
flagOpt = false;
textBox1.Text += "\r\nСреди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи." +
"\r\nОкончательный вариант симплекс-таблицы:";
print(tab, x, y);
textBox1.Text += "\r\nОптимальный план можно записать так:\r\n";
for (j = 0; j < n; j++)
for (i = 0; i < m; i++)
if (basisA[i] == j + 1)
{
AnswerA[j] = bA[i];
C[0, i] = 1;
}
for (i = 0; i < n; i++)
textBox1.Text += "x" + (i + 1) + " = " + AnswerA[i] + "\r\n";
textBox1.Text += "\r\nF(X)=";
for (i = 0; i < n; i++)
{
valueFA += 1 * AnswerA[i];
textBox1.Text += "1 * " + AnswerA[i] + "+";
}
textBox1.Text += "= " + valueFA;
textBox1.Text += "\r\n\nСоставим двойственную задачу к прямой задаче:";
print(sourceB, n, m);
textBox1.Text += "\r\nИспользуя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи."
+ "\r\nИз теоремы двойственности следует, что Y = C*A^(-1). "
+ "\r\nСоставим матрицу A из компонентов векторов, входящих в оптимальный базис." +
"\r\nА=(";
for (i = 0; i < m; i++)
textBox1.Text += "A" + basisA[i] + ", ";
textBox1.Text += ")=";
float[,] matrA = new float[m, m];
h = 0;
bool flagMatr = false;
for (i = 0; i < m; i++)
{
flagMatr = false;
for (j = 0; j < n; j++)
if (basisA[i] == j + 1)
{
for (k = 0; k < m; k++) matrA[k, h] = sourceB[j, k];
h++;
flagMatr = true;
}
if (!flagMatr)
{
for (k = 0; k < m; k++) matrA[k, h] = tab[k, basisA[i]];
h++;
}
}
print(matrA, m, m);
textBox1.Text += "Определив обратную матрицу А^(-1) по методу Жордано-Гаусса, получим:";
float[,] obr = new float[m, m];
obr = obrMatrFunction(matrA, m);
print(obr, m, m);
textBox1.Text += "Как видно из последнего плана симплексной таблицы, обратная матрица A^(-1) " +
"расположена в столбцах дополнительных переменных.\r\nТогда Y = C*A^(-1)= \r\n(";
for (i = 0; i < m; i++)
textBox1.Text += C[0, i] + ", ";
textBox1.Text += ")X";
print(obr, m, m);
AnswerB = multiplication(C, obr);
textBox1.Text += "=(";
for (i = 0; i < m; i++)
textBox1.Text += AnswerB[0, i] + ", ";
textBox1.Text += ")\r\nОптимальный план двойственной задачи равен:\r\n";
for (i = 0; i < m; i++)
textBox1.Text += "y" + (i + 1) + " = " + AnswerB[0, i] + "\r\n";
textBox1.Text += "\r\nZ(Y)=";
for (i = 0; i < m; i++)
{
valueFB += 1 * AnswerB[0, i];
textBox1.Text += "1 * " + AnswerB[0, i] + "+";
}
textBox1.Text += "= " + valueFB;
textBox1.Text += "\r\nКритерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y)," +
"то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно.";
};
Label2: ;
}
}
else textBox1.Text += "задача неразрешима";
}
// Функция для определения максимального элемента в массиве
public void maximum(float[] arr, ref int arrmaxpos)
{
int i;
float arrmax;
arrmax = arr[1];
arrmaxpos = 1;
for (i = 1; i < arr.Length; i++)
if (arr[i] > arrmax)
{
arrmax = arr[i];
arrmaxpos = i;
}
}
// Функция для определения минимельного элемента в массиве
public void minimum(float[] arr, ref int arrminpos)
{
int i;
float arrmin;
arrmin = arr[0];
arrminpos = 0;
for (i = 0; i < arr.Length; i++)
if (arr[i] < arrmin)
{
arrmin = arr[i];
arrminpos = i;
}
}
// Функция для определения минимельного элемента в строке
public void minimumA(float[] arr, float[] f, ref int arrminpos)
{
int i;
float arrmin;
arrmin = 9999999;
arrminpos = 0;
for (i = 0; i < arr.Length; i++)
if ((arr[i] < 0) & (f[i + 1] != 0) & (f[i + 1] / arr[i] < arrmin))
{
arrmin = f[i + 1] / arr[i];
arrminpos = i;
}
}
// Функция для определения минимельного элемента в столбце
public void minimumA2(float[] b, float[] a, ref int arrminpos)
{
int i;
float arrmin;
arrmin = 9999999;
arrminpos = 0;
for (i = 0; i < a.Length; i++)
if ((b[i] / a[i] < arrmin) & ((b[i] / a[i] > 0)))
{
arrmin = b[i] / a[i];
arrminpos = i;
}
}
// Функция вычисления обратной матрицы методом Жордано-Гаусса
public float[,] obrMatrFunction(float[,] matrA, int m)
{
int i = 0, j = 0, k = 0;
float[,] matrAx2 = new float[m, 2 * m];
float[,] tempMatrAx2 = new float[m, 2 * m];
float[,] obrMatrA = new float[m, m];
float[,] matrB = new float[m, m];
for (i = 0; i < m; i++)
for (j = 0; j < m; j++)
matrB[i, j] = matrA[i, j];
float det;
det = detMatr(matrB, m);
textBox1.Text += det;
if (det != 0)
{
for (i = 0; i < m; i++)
for (j = 0; j < m; j++)
{
matrAx2[i, j] = matrA[i, j];
if (i == j)
matrAx2[i, j + m] = 1;
}
print(matrAx2, m, 2 * m);
// Пересчет симплексной таблицы методом Жордано-Гаусса
for (k = 0; k < m; k++)
{
for (i = 0; i < 2 * m; i++)
tempMatrAx2[k, i] = matrAx2[k, i] / matrAx2[k, k];
for (i = 0; i < m; i++)
for (j = 0; j < 2 * m; j++)
if (i != k)
{
tempMatrAx2[i, j] = matrAx2[i, j] - (matrAx2[k, j] * matrAx2[i, k] / matrAx2[k, k]);
}
for (i = 0; i < m; i++)
for (j = 0; j < 2 * m; j++)
matrAx2[i, j] = tempMatrAx2[i, j];
print(tempMatrAx2, m, 2 * m);
}
print(tempMatrAx2, m, 2 * m);
for (i = 0; i < m; i++)
for (j = m; j < 2 * m; j++)
obrMatrA[i, j - m] = matrAx2[i, j];
print(obrMatrA, m, m);
return obrMatrA;
}
else
{
textBox1.Text += "Определитель равен 0. Матрица имеет бесконечное множество решений";
return null;
}
}
// Функция умножения матриц
public float[,] multiplication(float[,] a, float[,] b)
{
if (a.GetLength(1) != b.GetLength(0)) throw new Exception("Матрицы нельзя перемножить");
float[,] r = new float[a.GetLength(0), b.GetLength(1)];
for (int i = 0; i < a.GetLength(0); i++)
{
for (int j = 0; j < b.GetLength(1); j++)
{
for (int k = 0; k < b.GetLength(0); k++)
{
r[i, j] += a[i, k] * b[k, j];
}
}
}
return r;
}
// Обработка нажатия кнопки "Подробное решение"
private void button1_Click(object sender, EventArgs e)
{
DetailSolutionForm f = new DetailSolutionForm( Data.n, Data.m);
f.ShowDialog();
}
// Обработка нажатия кнопки "По умолчанию"
private void defaultBtn_Click(object sender, EventArgs e)
{
// матрица по умолчанию
Data.solText = " ";
Data.answer = " ";
textBox1.Clear();
textBox2.Clear();
exampleGrd.Columns.Clear();
int[,] a = new int[4, 5] { { 50, 80, 70, 50, 40 }, { 10, 10, 50, 50, 60 }, { 20, 40, 30, 60, 20 }, { 30, 50, 40, 40, 30 } };
for (int i = 0; i < 5; i++) exampleGrd.Columns.Add("", "B" + (i + 1));
for (int j = 0; j < 4; j++)
{
exampleGrd.Rows.Add();
exampleGrd.Rows[j].HeaderCell.Value = "A" + (j + 1);
}
for (int j = 0; j < 5; j++)
for (int i = 0; i < 4; i++)
exampleGrd[j, i].Value = a[i, j];
exampleGrd.AutoResizeColumns();
detailSolBtn.Enabled = false;
solutionBtn.Enabled = true;
}
// Функция для определения вывода данных массива
public void print(float[,] mas, int x, int y)
{
int i = 0, j = 0;
textBox1.Text += "\r\n";
for (i = 0; i < x; i++)
{
for (j = 0; j < y; j++)
{
textBox1.Text += mas[i, j] + " ";
}
textBox1.Text += "\r\n";
}
}
}
// Статический класс, который доступен из всех наследуемых форм приложения
static class Data
{
public static string solText { get; set; }
public static string answer { get; set; }
public static float[,] sourceA { get; set; }
public static float[,] a { get; set; }
public static float[,] a1 { get; set; }
public static float[,] a2 { get; set; }
public static int n { get; set; }
public static int m { get; set; }
}
}