1 Итерация

1) Проверка критерия оптимальности

План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.

2) Определение новой свободной переменной

Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 1-ая строка, а переменную x₃ следует вывести из базиса.

3) Определение новой базисной переменной

Минимальное значение θ соответствует 1-му столбцу, т.е. переменную x₁ необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-50) (табл. 3.7).

Таблица 3.7 – Определение разрешающего элемента при первой итерации

Базис	B	x1	x2	x3	x4
x3	-1	-50	-10	1	0
x4	-1	-40	-60	0	1
F(X0)	0	-1	-1	0	0
θ	0	-1 : (-50) = 1/50	-1 : (-10) = 1/10	-	-

4) Пересчет симплекс-таблицы

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса (табл. 3.8).

Таблица 3.8 – Итоговая таблица после первой итерации

Базис	B	x1	x2	x3	x4
x1	1/50	1	1/5	-1/50	0
x4	-1/5	0	-52	-4/5	1
F(X0)	1/50	0	-4/5	-1/50	0

Представим расчет каждого элемента в таблице 3.9:

Таблица 3.9 – Таблица с расчетами для каждого элемента

B	x 1	x 2	x 3	x 4
-1 : -50	-50 : -50	-10 : -50	1 : -50	0 : -50
-1-(-1 • -40):-50	-40-(-50 • -40):-50	-60-(-10 • -40):-50	0-(1 • -40):-50	1-(0 • -40):-50
0-(-1 • -1):-50	-1-(-50 • -1):-50	-1-(-10 • -1):-50	0-(1 • -1):-50	0-(0 • -1):-50

2 Итерация

1. Проверка критерия оптимальности

План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец.

2) Определение новой свободной переменной

Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 2-ая строка, а переменную x₄ следует вывести из базиса.

3) Определение новой базисной переменной

Минимальное значение θ соответствует 2-му столбцу, т.е. переменную x₂ необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-52) (табл. 3.10).

Таблица 3.10 – Определение разрешающего элемента при второй итерации

Базис	B	x1	x2	x3	x4
x1	1/50	1	1/5	-1/50	0
x4	-1/5	0	-52	-4/5	1
F(X0)	1/50	0	-4/5	-1/50	0
θ	0	-	-4/5 : (-52) = 1/65	-1/50 : (-4/5) = 1/40	-

4) Пересчет симплекс-таблицы

Выполняем преобразования симплексной таблицы методом Жордано-Гаусса (табл. 3.11).

Таблица 3.11 – Итоговая таблица после первой итерации

Базис	B	x1	x2	x3	x4
x1	1/52	1	0	-3/130	1/260
x2	1/260	0	1	1/65	-1/52
F(X1)	3/130	0	0	-1/130	-1/65

В базисном столбце все элементы положительные.

Переходим к основному алгоритму симплекс-метода.

1) Проверка критерия оптимальности

Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.

Окончательный вариант симплекс-таблицы (табл. 3.12):

Таблица 3.12 - Окончательный вариант симплекс-таблицы

Базис	B	x1	x2	x3	x4
x1	1/52	1	0	-3/130	1/260
x2	1/260	0	1	1/65	-1/52
F(X1)	3/130	0	0	-1/130	-1/65

Оптимальный план можно записать так:

x₁ = ¹/₅₂

x₂ = ¹/₂₆₀

F(X) = 1•¹/₅₂ + 1•¹/₂₆₀ = ³/₁₃₀

Составим двойственную задачу к прямой задаче:

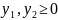
Используя последнюю итерацию прямой задачи, найдем оптимальный план двойственной задачи.

Из теоремы двойственности следует, что

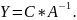
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Определив обратную матрицу по методу Жордано-Гаусса, получим:

Как видно из последнего плана симплексной таблицы, обратная матрица расположена в столбцах дополнительных переменных.

Тогда

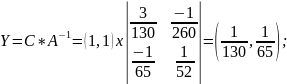
Оптимальный план двойственной задачи равен:

y₁ = ¹/₁₃₀

y₂ = ¹/₆₅

Z(Y) = 1•¹/₁₃₀ + 1•¹/₆₅ = ³/₁₃₀

Так как F(x) = Z(y), то решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно.

Шаг 5. Определим цену игры и вероятности применения стратегий фирм.

Цена игры:

Вероятности применения стратегий A₁, A₂, A₃, A₄ фирмой А:

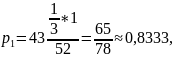
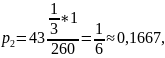
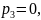
Цена игры:

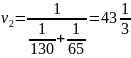
Вероятности применения стратегий B₁, B₂, B₃, B₄, B₅ фирмой B:

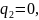
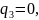
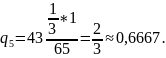
Истинная цена игры: .
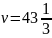