2.4 Проектирование сценария диалога

Подсистема диалога реализует основные функции по управлению программой пользователем, ввод данных задачи (количество стратегий для фирм А и В, платежная матрица), отображение результатов в виде ответа и подробного решения. Формы программы, реализующие перечисленные функции изображены на рисунках 2.1 – 2.4.

Пользователь может выбирать количество стратегий для фирм А и В и задавать платежную матрицу, а может воспользоваться контрольным примером, нажав кнопку “По умолчанию” (рис. 2.3). Для того чтобы получить решение задачи, необходимо нажать кнопку «Решить». Результат можно увидеть на рисунке 2.2. Для получения подробного решения необходимо нажать кнопку «Подробное решение» (рис. 2.4).

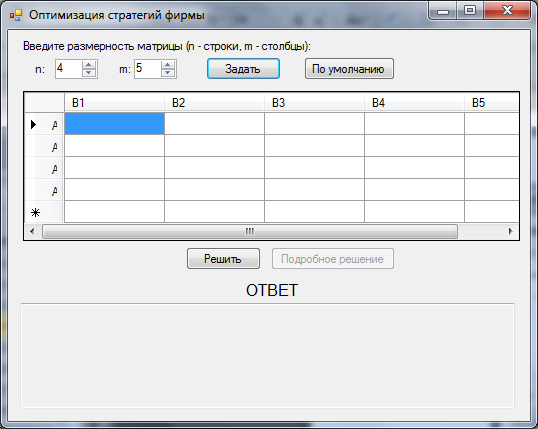
Рисунок 2.1 – Основное окно программы при вводе данных

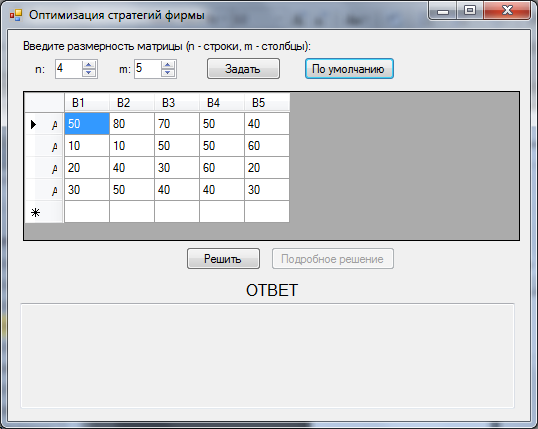
Рисунок 2.2 – Основное окно программы при задании данных по умолчанию

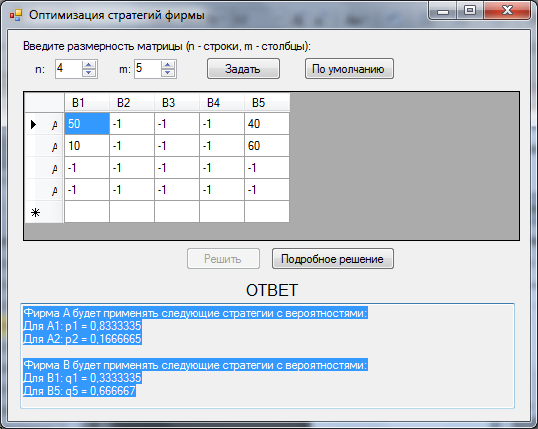
Рисунок 2.3 – Основное окно программы после решения задачи

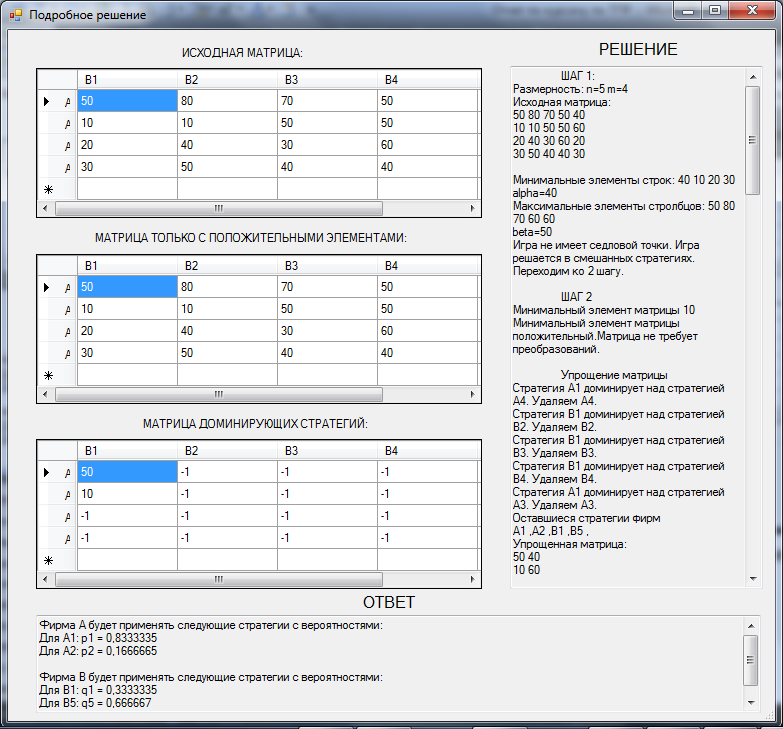
Рисунок 2.4 – Окно программы с подробным решением задачи

2.5 Описание структур данных

Программа состоит из 3 классов, описанных ниже:

• MainForm – форма WindowsFrom основного окна программы;

• DetailSolutionForm – форма WindowsFrom окна программы с подробным решением;

• Data – класс для хранения и использования глобальных переменных программы.

В таблице 2.2 приведено описание методов класса MainForm.

Таблица 2.2 – Описание методов классов

Название метода	Описание метода
razmerBtn_Click	Обработчик события по нажатию кнопки "Задать"
solutionBtn_Click	Обработчик события по нажатию кнопки "Решить"
button1_Click	Обработчик события по нажатию кнопки “Подробное решение”
defaultBtn_Click	Обработчик события по нажатию кнопки “ По умолчанию”
solution	Функция, реализующая основной алгоритм программы
detMatr	Функция расчёта определителя матрицы
simplexMethod	Функция для решения ЗЛП двойственным симплекс-методом
maximum	Функция для определения максимального элемента в массиве
minimum	Функция для определения минимельного элемента в массиве
minimumA	Функция для определения минимельного элемента в строке
minimumA2	Функция для определения минимельного элемента в столбце
obrMatrFunction	Функция вычисления обратной матрицы методом Жордано-Гаусса
multiplication	Функция умножения матриц
print	Функция для определения вывода данных массива

Листинг программы представлен в приложении A.

2.6 Структура программной системы

Структурная схема программной системы приведена на рисунке 2.5.

Рисунок 2.5 – Структурная схема основного алгоритма

2.7 Структурная схема алгоритма сценария диалога и описание его программной реализации.

Структурная схема основного алгоритма программы приведена на рисунке 2.6.

Рисунок 2.6 – Структурная схема основного алгоритма

2.8 Структурная схема функциональных алгоритмов и описание их программной реализации

Структурная схема алгоритма двойственного симплекс-метода представлена на рисунке 2.7.

Рисунок 2.7 – Структурная схема алгоритма двойственного симплекс-метода

3 ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

3.1 Ручная реализация алгоритма решения задачи

Исходные данные:

Две конкурирующие фирмы А и В выпускают однотипные товары. Для обеспечения наибольшей прибыли обе фирмы разработали стратегии реализации своих товаров. Фирма А разработала четыре стратегии: А1, А2, А3, А4. Фирма В – пять стратегий: В1, В2, В3, В4, В5. Доход фирмы А от реализации Ai своих стратегий при стратегиях фирмы В – Bj равен Cij. Найти оптимальную стратегию для фирмы А (табл. 3.1).

Таблица 3.1 – Доход фирмы А

Стратегии	В1	В2	В3	В4	В5
А1	50	80	70	50	40
А2	10	10	50	50	60
А3	20	40	30	60	20
А4	30	50	40	40	30

Решение задачи:

Шаг 1. Определим минимальную прибыль фирмы А при каждой своей стратегии и максимальный убыток фирмы В при этом (табл. 3.2).

Таблица 3.2 - Возможные минимальные прибыли и максимальные убытки фирм

Стратегии	В1	В2	В3	В4	В5	Минимальная прибыль фирмы А
А1	50	80	70	50	40	40
А2	10	10	50	50	60	10
А3	20	40	30	60	20	20
А4	30	50	40	40	30	30
Максимальный убыток фирмы В	50	100	70	60	60

Нижняя цена игры (гарантированный минимальный доход фирмы А) составит α = 40, а верхняя цена игры (минимально возможный убыток, который понесет фирма В) составит β = 50. Так как α ≠ β, то игра не имеет седловой точки и, следовательно, не решается в чистых стратегиях.

Шаг 2. Решаем игру в смешанных стратегиях. Для этого в таблице (платежной матрице) находится минимальный элемент, равный 10. Так как он положительный, то матрица не требует преобразований. Переходим к её упрощению.

Строка (стратегия) А1 является доминирующей по отношению к строке (стратегии) А4 , так как содержит элементы, большие соответствующих элементов строки А4 . Соответственно строка А4 является поглощаемой и из дальнейшего рассмотрения удаляется (табл. 3.3).

Таблица 3.3 - Первый шаг упрощения таблицы

Стратегии	В1	В2	В3	В4	В5
А1	50	80	70	50	40
А2	10	100	50	50	60
А3	20	40	30	60	20

Первый столбец является доминирующим по отношению ко второму, третьему и четвертому столбцам (поглощаемым). Поступаем аналогично (табл. 3.4).

Таблица 3.4 - Второй шаг упрощения таблицы

Стратегии	В1	В5
А1	50	40
А2	10	60
А3	20	20

Еще раз рассматриваем строки. Первая строка поглощает третью строку. Поглощаемые строки (столбцы) содержат самые плохие стратегии. Окончательно получим (табл. 3.5).

Таблица 3.5 – Третий шаг упрощения таблицы

Стратегии	В1	В5
А1	5	4
А2	1	6

Шаг 3. Для преобразованной платежной матрицы формируется задача линейного программирования для фирмы А:

Шаг 4. Решим прямую задачу линейного программирования двойственным симплексным методом, с использованием симплексной таблицы.

Приведем систему ограничений к системе неравенств смысла ≤, умножив соответствующие строки на (-1).

Определим минимальное значение целевой функции F(X) = x₁ + x₂ при следующих условиях-ограничениях.

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄.

-50x₁-10x₂ + 1x₃ + 0x₄ = -1

-40x₁-60x₂ + 0x₃ + 1x₄ = -1

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных: x₃, x₄.Полагая, что свободные переменные равны 0, получим первый опорный план (табл. 3.6):

X1 = (0,0,-1,-1)

Базисное решение называется допустимым, если оно неотрицательно.

Таблица 3.6 – Первая итерация

Базис	B	x1	x2	x3	x4
x3	-1	-50	-10	1	0
x4	-1	-40	-60	0	1
F(X0)	0	-1	-1	0	0