2 Алгоритмизация решения задачи

2.1 Анализ методов решения задачи

Для вычисления значений смешанных стратегий можно использовать метод линейного программирования либо итерационный метод.

Итерационный метод позволяет получить приближенное решение матричной игры в смешанных стратегиях. Суть метода состоит в том, что произ­водится имитация игры, предполагающая последовательный выбор стратегий ка­ждым из игроков. Выбор стратегии игроком А основан на достижении макси­мального выигрыша, а игрок В исходит из условия выбора той стратегии, которая обеспечивает минимизацию проигрыша. Каждому игроку поочередно предостав­ляется право выполнить ход, совокупность двух ходов противников образует пар­тию, по окончанию каждой из партии вычисляются статистические оценки ниж­ней и верхней цен игры, а также среднее значение цены игры. По окончании итерационного процесса производится расчет оценок вероятностей применения стратегий.

При решении матричной игры также можно перейти к задаче линейного программирования. Решив её и подставив полученные значения в соответствующие формулы, можно найти вероятности применения стратегий каждым из игроков.

2.2 Выбор и описание метода

В данной курсовой работе решение матричной игры в смешанных стратегиях производится с помощью перехода к задаче линейного программирования. Выбор в пользу этого метода был сделан потому, что при использовании итерационного метода для получения более-менее точного итогового результата необходимо произвести большое количество итераций.

Метод линейного программирования же позволяет найти точный результат, вычисления при ручном расчете получаются не такими громоздкими, и шанс ошибиться в расчетах уменьшается.

Саму задачу линейного программирования удобно решать с помощью двойственного симплекс-метода.

Решение матричной игры в смешанных стратегиях с помощью перехода к задаче линейного программирования.

Предположим, что цена игры положительна ( > 0). Если это не так, то всегда можно подобрать такое число μ, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами и, следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.

Свойство 1. Тройка (хо, yо, ) является решением игры G = (Х,Y,А) тогда и только тогда, когда (хо, yо, к +а) является решением игры G(Х,Y,кА+а), где а – любое вещественное число, к > 0.

Свойство 2. Для того, чтобы х_о = ( ) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры , необходимо и достаточно выполнение следующих неравенств

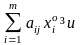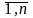(j = ) (2.2.1)

Аналогично для игрока 2: чтобы y_о = (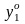 , ..., , ...,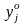 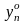) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:

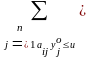(i = ) (2.2.2)

Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, y) и  решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (2.2.1) и (2.2.2). С другой стороны, найдя неотрицательные решения неравенств (2.2.1) и (2.2.2) совместно со следующими уравнениями

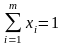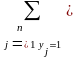, (2.2.3)

получим решение матричной игры.

Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 2 оптимальные смешанные стратегии х = (х1, ..., хm), y = (y1, ..., yn) соответственно игроков 1 и 2 и цена игры  должны удовлетворять соотношениям.

(2.2.4)

(2.2.5)

Разделим все уравнения и неравенства в (2.2.4) и (2.2.5) на  (это можно сделать, т.к. по предположению  > 0) и введём обозначения:

, ,

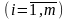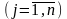Тогда (2.2.1) и (2.2.2) перепишется в виде:

, , , ,

, , , .

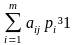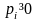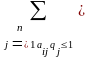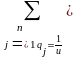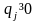Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i , чтобы цена игры  была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений p_i , при которых

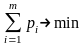, . (2.2.6)

Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена игры  была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений q_j, , при которых

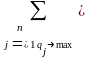, . (2.2.7)

Формулы (2.2.6) и (2.2.7) выражают двойственные друг другу задачи линейного программирования (ЛП).

Решив эти задачи, получим значения p_i, , q_j, и . Тогда смешанные стратегии, т.е. xi и yj получаются по формулам:

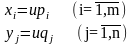(2.2.8)