Функция регрессии

Если функциональная зависимость между двумя показателями неизвестна, обычно пытаются установить тесноту их связи, измерить степень их зависимости. При этом прибегают к методамкорреляционно-регресионного анализа.

Пусть х – независимая переменная, у – зависимая переменная.

Зависимость х от у называется функциональной, если каждому значению х соответствует единственное значение у (при этом и х и у могут быть как детерминированными, так и случайными).

Если каждому фиксированному значению х соответствует множество у, мы имеемстохастическую зависимость. Среднее значение (групповое генеральное среднее) этого множества (при х = х) называется математическим ожиданием случайной величины у, вычисленным при условии, что  х = х.

Таким образом, необходимо выяснить, изменяются или нет при изменении х условные математические ожидания М(У/Х=х). Если изменяются, то имеет место корреляционная зависимость у от х, если нет, то отсутствует.

Функция регрессии. Функция f(x) = M(У/Х=х), описывающая изменение условного математического ожидания случайной переменной У при изменении значений х переменной Х, называется функцией регресии.

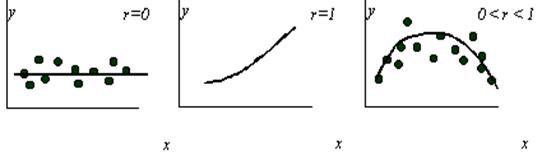
Обычно используют коэффициент парной корреляции или генеральное корреляционное отношение, который может изменяться от 0 до 1 или от –1 до 1 (коэффициент парной корреляции).

Коэффициент корреляции может отличаться от 0 в следующих случаях:

1)      У причинно зависит от Х;

2)      Х причинно зависит от У;

3)      У и Х непосредственно не влияют друг на друга, но совместно зависят от одного или нескольких факторов, причинно влияющих на Х и У;

4)      Имеет место простое совпадение согласованности изменений х и у.

Само по себе установление причинно-следственных связей является важной задачей. Используются различные способы формирования связей между внешними факторами и показателями системы. Например, может быть использован экспертный метод с привлечением коллективов экспертов разных специальностей.

Корреляционный анализ занимается степенью связи между двумя случайными величинами Х и Y.

Корреляционный анализ экспериментальных данных для двух случайных величин заключает в себе следующие основные приемы:  1. Вычисление выборочных коэффициентов корреляции.  2. Составление корреляционной таблицы.  3. Проверка статистической гипотезы значимости связи.

ОПРЕДЕЛЕНИЕ. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии.

Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости оценить ее силу по величине коэффициента регрессии. Например, ясно, что корреляционная зависимость возраста Y учеников средней школы от года Х их обучения в школе является, как правило, более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возраcте, чем у школьников одного и того же класса.

Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции, определяемого формулой:

 (7)

где σ_X и σ_Y выборочные средние квадратические отклонения величин Х и Y, которые вычисляются по формулам:

 (8)

Следует отметить, что основной смысл выборочного коэффициента линейной корреляции r_B состоит в том, что он представляет собой эмпирическую (т.е. найденную по результатам наблюдений над величинами Х и Y) оценку соответствующего генерального коэффициента линейной корреляции r: r=r_B(9)

Принимая во внимание формулы:

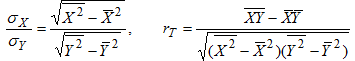
видим, что выборочное уравнение линейной регрессии Y на Х имеет вид:

 (10)

где  . То же можно сказать о выборочном уравнений линейной регрессии Х на Y:

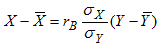 (11)