5.3.2. Апериодический регулятор повышенного порядка
Если увеличить конечное время установления на один такт с m до m + 1, то можно заранее определить начальное значение управляющей переменной u(0). Поскольку этот сигнал обычно имеет максимальную величину, его можно ограничить, задав допустимое значение u(0) при синтезе регулятора.
Добавим еще один член в уравнения (5.40) и (5.41), тогда уравнения (5.42) и (5.43) примут вид
,
(5.61)
(5.62)
Приравнивая коэффициенты этих полиномов коэффициентам из уравнения (5.49), получим
(5.63)
Это равенство справедливо только в том случае, когда его правая часть содержит общий корень в числителе и знаменателе.
Таким образом,
.
(5.64)
После деления на q1'0, получим связь между коэффициентами уравнения (5.64) и (5.63):
(5.65)
Теперь выпишем параметры полных полиномов числителя и знаменателя уравнения (5.64) и, приравнивая коэффициенты в правых частях уравнений (5.63) и (5.64), получим следующие соотношения:
(5.66)
Из уравнения (5.43) имеем
,
(5.67)
а из уравнений (5.61) или (5.42) получим
p1 + … + pm+1 = 1.
Наконец, из уравнений (5.66) и (5.65) следует, что
.
(5.68)
Теперь на основании уравнений (5.67) и (5.68) можно записать соотношения для определения параметров регулятора:
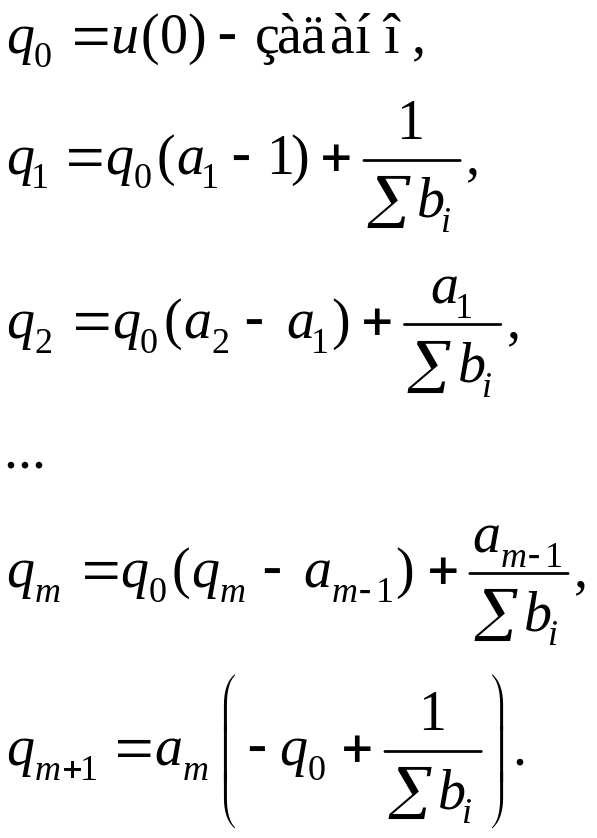(5.69)
(5.70)
По аналогии с уравнением (5.50) запишем передаточную функцию регулятора
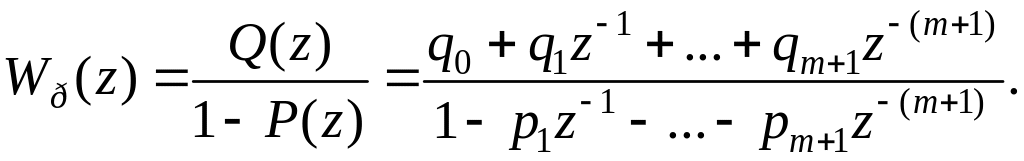(5.71)
Однако в отличие от регулятора, описываемого выражением (5.50), в данном случае начальное значение управляющей переменной u(0) задано. Второе значение управляющей переменной в соответствии с уравнениями (5.43) и (5.69) будет равно
.
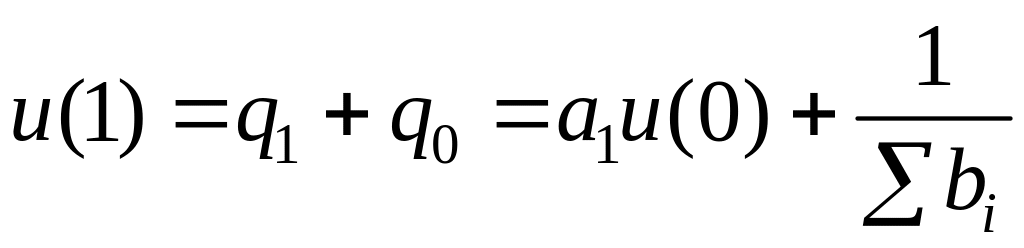(5.72)
Значение u(0) не следует задавать слишком малым, так как при этом u(1) > u(0), что в большинстве случаев нежелательно.
Для выполнения условия u(l) u(0) необходимо, чтобы удовлетворялось соотношение
.
(5.73)
Выполнение условия u(l) u(0) вовсе не гарантирует, что |u(k)| < < |u(0)| для k 2. Поскольку расчет параметров регулятора достаточно прост, значение u(0) обычно изменяют до тех пор, пока не будет получена желаемая последовательность управляющих сигналов. Часто условие u(l) = u(0) приводит к хорошим результатам.
Для объектов с запаздыванием (d > 0) расчет регулятора выполняют с использованием уравнений (5.53 5.57). В этом случае передаточная функция апериодического регулятора AP(v + l), определяемая уравнением (5.71) и соотношениями (5.69) и (5.70), принимает вид
,
(5.74)
где
.
(5.75)
Характеристическое уравнение регулятора записывается следующим образом:
.
(5.76)
5.4. Синтез системы управления с заданным расположением полюсов
5.4.1. Синтез по заданному расположению полюсов с помощью обратной связи по состоянию (случай единственного управляющего сигнала)
Пусть требуется, чтобы система в переменных состояниях, замкнутая управлением (GX) имела желаемые корни характеристического уравнения. Нужно найти матрицу G
Введем следующие обозначения:
матрица
преобразования сигнала; (5.77)
матрица
преобразования
сигнала управления в замкнутой системе; (5.78)
разностная матрица
сигнала управления; (5.79)
характеристическое
уравнение матрицы А
(разомкнутой системы); (5.80)
характеристическое
уравнение матрицы
А – ВG (замкнутой системы); (5.81)
(5.82)
В этих выражениях I обозначает единичную матрицу соответствующей размерности.
Сначала покажем, что
(5.83)
Для этого запишем
(5.84)
Вычисляя определители обеих частей последнего уравнения, получим
(5.85)
Поскольку
(5.86)
где единичные матрицы имеют различные размерности, выражение (5.85) принимает вид
(5.87)
Таким образом, соотношение (5.83) доказано.
Важную роль играет следующее функциональное соотношение:
(5.88)
или
(5.89)
Применяя операцию обращения матриц к обеим частям уравнения (5.89), получим
(5.90)
Умножение обеих частей уравнения (5.90) слева на
I + (zI A)1BG дает
(5.91)
Теперь, умножая обе части (5.91) слева на G и справа на В, получим
(5.92)
Последнее выражение запишем иначе:
(5.93)
Таким образом, соотношение (5.89) доказано.
Последнее необходимое нам соотношение получим, используя выражения (5.79) и (5.77). Запишем (5.79) в виде
(5.94)
где Adj (zI A) матрица, присоединенная к матрице zI А.
Пусть
(5.95)
Тогда (5.94) примет вид
(5.96)
Откуда следует, что Т(z) есть скалярная функция.
Используя выражение (5.87) и учитывая (5.82), приведем последнее соотношение к виду
(5.97)
Таким образом, если известны k(z), c(z) и 0(z), то из (5.97) мы можем найти решение для матрицы коэффициентов обратной связи G в случае, когда пара матриц [А, В] полностью управляема.
Выражение для G может быть получено через желаемые собственные значения замкнутой системы. Пусть среди этих собственных значений z1, z2, z3, …, zm различные, а все остальные являются кратными, тогда
(5.98)
И, следовательно, из выражения (5.97) вытекает
(5.99)
Обозначим
(5.100)
(5.101)
Тогда i = 1, 2, …, m; (5.99) примет вид
(5.102)
В случае собственного значения кратности q продифференцируем обе части выражения (5.102) по z и, полагая z = zm+j, j = 1,2,…, q, получим
(5.103)
где
(5.104)
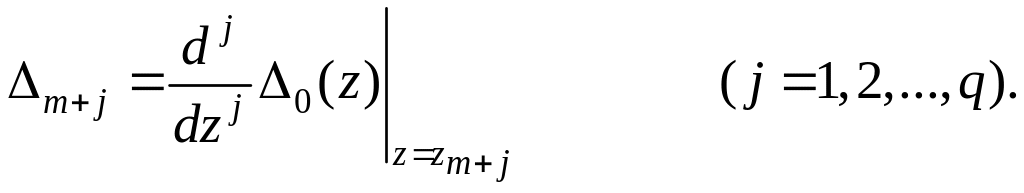(5.105)
Для всех n собственных значений имеем
