5.3.1. Обычный апериодический регулятор

Предполагается, что ступенчатое изменение задающей переменной происходит в момент времени k = 0, т. е.

(k) = 1 для k = 0, 1, 2, … (5.37)

Если время запаздывания d = 0, то требования для минимального конечного времени установления переходного процесса записываются следующим образом:

для ,

для . (5.38)

Для случая b₀ = 0 z-преобразования задающей, регулируемой и управляющей переменных имеют следующий вид:

, (5.39)

, (5.40)

. (5.41)

Разделив уравнения (5.40) и (5.41) на (5.39), получим

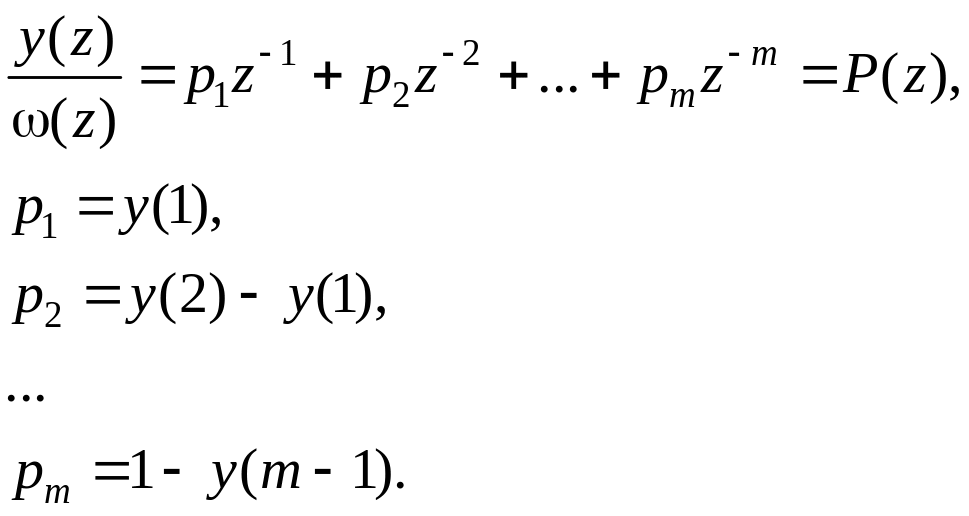(5.42)

(5.43)

Следует учесть, что

p₁ + p₂ + … + p_m = 1, (5.44)

. (5.45)

Передаточная функция замкнутой системы будет равна

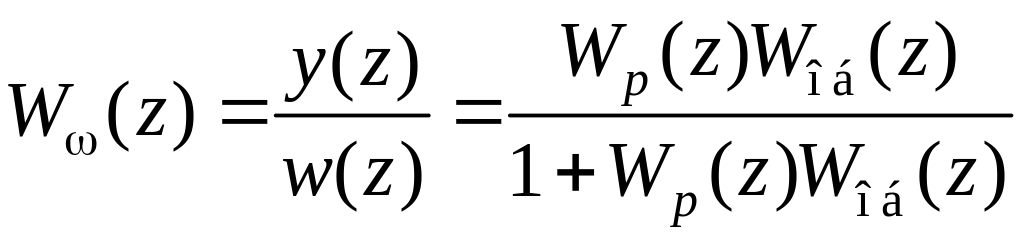. (5.46)

Следовательно, передаточная функция компенсационного регулятора имеет вид

. (5.47)

Сравнивая уравнения (5.42) и (5.46), получим

. (5.48)

Более того, из уравнений (5.42) и (5.43) следует, что

, (5.49)

и с учетом (5.47) передаточная функция регулятора принимает вид

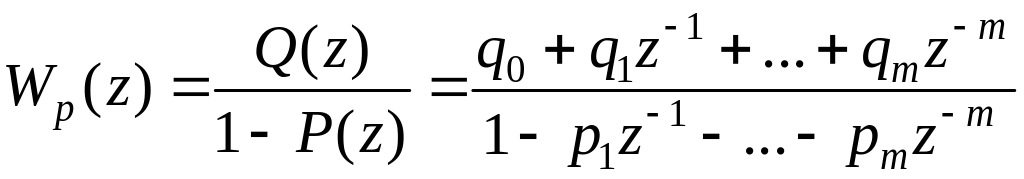. (5.50)

Параметры этого регулятора можно получить, используя уравнения (5.49), (5.44) и (5.45):

,

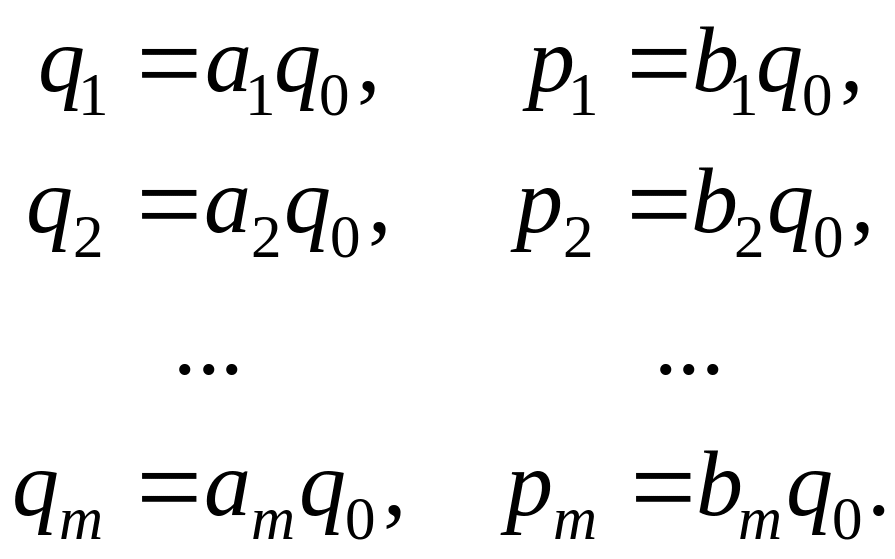(5.51)

Таким образом, параметры регулятора могут быть вычислены достаточно просто. Начальное значение управляющей переменной u(0) зависит только от значения суммы коэффициентов b₁ объекта. Поскольку значение этой суммы убывает с уменьшением такта квантования, начальное значение управляющей переменной u(0) будет тем больше, чем меньше такт квантования.

Такой апериодический регулятор можно считать компенсационным регулятором (см. 5.47), однако передаточную функцию замкнутой системы (5.44) и (5.42) в данном случае определяют в процессе проектирования, а не задают заранее. Результирующая передаточная функция замкнутой системы с учетом уравнений (5.48) и (5.42) принимает вид

Ее характеристическое уравнение равно

1 + W_p(z)W_об(z) = z^m = 0. (5.52)

Таким образом, контур управления с апериодическим регулятором имеет m полюсов в начале координат плоскости z.

Если d  0, необходимо использовать следующую модель объекта:

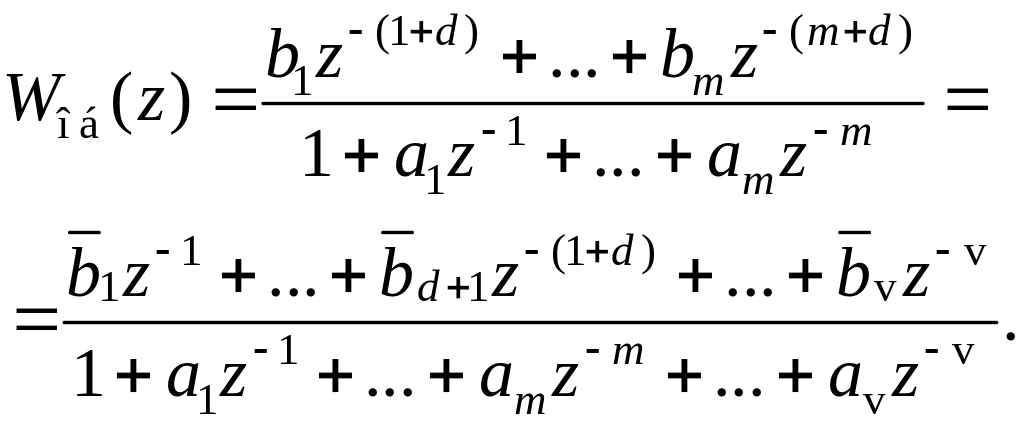(5.53)

Коэффициенты этой модели удовлетворяют соотношениям

(5.54)

На процесс управления наложены теперь следующие ограничения:

(5.55)

Далее можно применить уравнения (5.39)  (5.51), учитывая (5.53). Из уравнений (5.53) и (5.49) следует, что

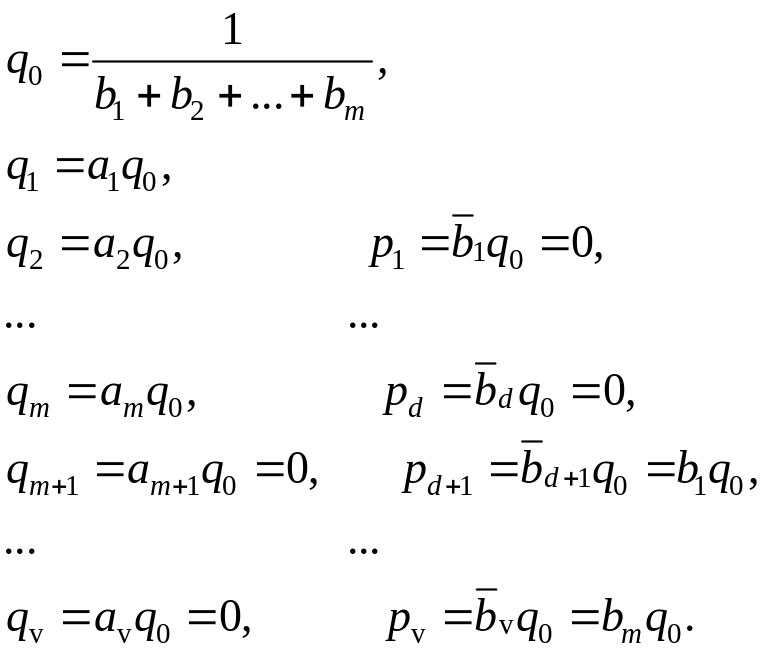(5.56)

Следовательно, передаточная функция регулятора имеет вид

. (5.57)

Из уравнений (5.56) и (5.57) получим передаточную функцию апериодического регулятора АР(v):

(5.58)

Отсюда следует, что передаточная функция по задающему сигналу при использовании точной модели объекта будет равна

, (5.59)

а ее характеристическое уравнение

(5.60)

что свидетельствует об апериодическом характере переходного процесса. Следует иметь в виду, что применение апериодического регулятора приводит к сокращению полюсов объекта управления.