
- •Глава 4. Анализ дискретных систем автоматического управления
- •4.1. Свойства дискретных систем
- •4.2. Преобразование и обработка сигналов
- •4.2.1. Математическое описание процесса квантования
- •4.3. Импульсная теорема
- •4.4. Фиксатор нулевого порядка
- •4.5. Элементы теории z-преобразования
- •4.5.1. Определение z-преобразования
- •4.5.2. Обратное z-преобразование
- •4.5.3. Теоремы z-преобразования
- •4.6. Импульсная передаточная функция
- •4.6.1. Последовательное соединение звеньев импульсных систем
- •4.6.2. Импульсная передаточная функция фиксатора нулевого порядка и связь между w(s) и w(z)
- •4.7. Процессы между моментами квантования
- •4.8. Метод пространства состояний
- •4.8.1. Уравнения состояния цифровых систем с квантованием и фиксацией
- •4.8.2. Уравнения состояния цифровых систем, содержащих только цифровые элементы
- •4.8.3. Переходные уравнения состояния цифровых систем
- •4.8.4. Переходные уравнения состояния цифровых стационарных систем
- •4.9. Устойчивость дискретных систем
- •4.9.1. Условия устойчивости
- •4.9.2. Критерии устойчивости
- •4.9.3. Робастность
- •4.9.4. Второй метод Ляпунова
- •4.10. Управляемость, достижимость и наблюдаемость
- •4.11. Процессы в нелинейных импульсных системах
- •4.11.1. Построение процессов
- •4.11.2. Вынужденные и свободные процессы
- •4.11.3. Возможные процессы
- •4.11.4. Влияние квантования по уровню
- •4.12. Устойчивость нелинейных импульсных систем
- •4.12.1. Понятие устойчивости
- •4.12.2. Условия абсолютной устойчивости
- •4.12.3. Критерий абсолютной устойчивости
- •4.13. Оценки качества свободных процессов
- •4.13.1. Мера быстродействия нелинейных импульсных систем
- •4.13.2. Оценка суммарного квадратического отклонения
- •Контрольные вопросы
4.5.3. Теоремы z-преобразования
Использование z-отображения часто может быть существенно облегчено применением теорем z-преобразования. Ниже приводятся доказательства основных теорем z-преобразования.
1.
Суммирование и вычитание.
Если
![]() и
и
![]() имеют z-преобразования:
имеют z-преобразования:
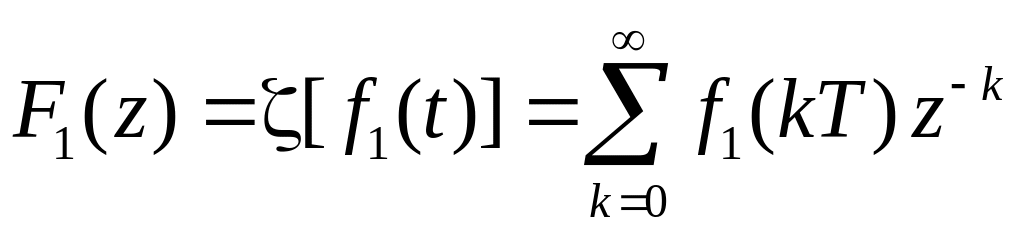 (4.92)
(4.92)
и
 (4.93)
(4.93)
то, соответственно,
![]() (4.94)
(4.94)
Д о к а з а т е л ь с т в о. Из определения z-преобразования следует:
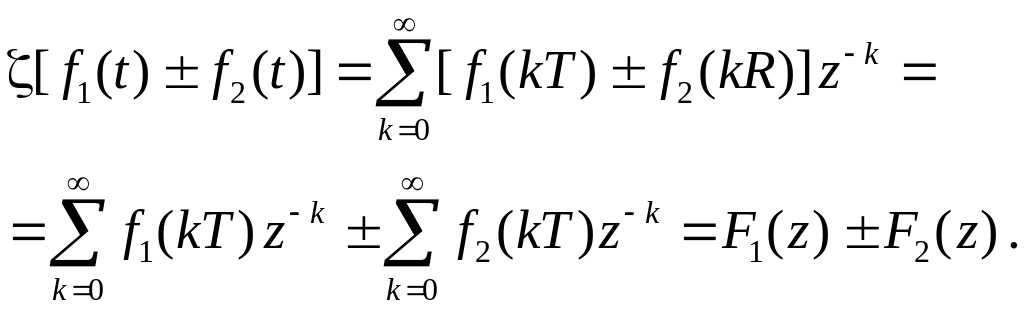 (4.95)
(4.95)
2.
Умножение на константу.
Если
![]() есть z-преобразование
есть z-преобразование
![]() ,
то
,
то
![]() (4.96)
(4.96)
где а – константа.
Д о к а з а т е л ь с т в о. Из определения z-преобразования следует:
 (4.97)
(4.97)
3. Сдвиг по временной области. Если имеет z-преобразование , то
![]() (4.98)
(4.98)
 (4.99)
(4.99)
где n – положительное целое число.
Д о к а з а т е л ь с т в о. По определению
 (4.100)
(4.100)
что может быть записано как
 (4.101)
(4.101)
Предполагая,
что
равно нулю при
![]() ,
получим выражение (4.101) в виде
,
получим выражение (4.101) в виде
 (4.102)
(4.102)
Для доказательства (4.101) запишем:
 (4.103)
(4.103)
4. Теорема об умножении оригинала на экспоненту (смещение в области изображений). Если имеет z-преобразование , то
![]() (4.104)
(4.104)
где а – константа.
Д о к а з а т е л ь с т в о. По определению
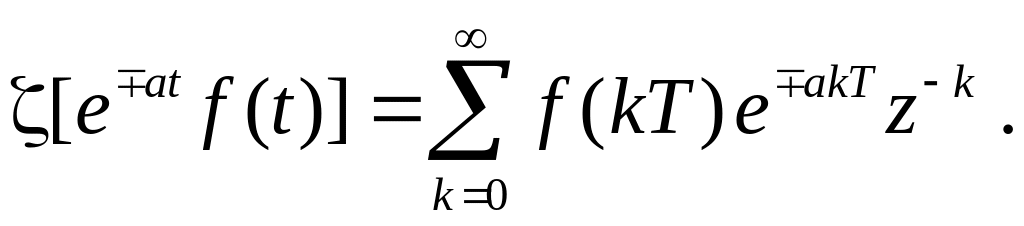 (4.105)
(4.105)
Положим
![]() ,
тогда выражение (4.105) запишем в виде
,
тогда выражение (4.105) запишем в виде
 (4.106)
(4.106)
Следовательно,
![]() (4.107)
(4.107)
5. Теорема о начальном значении. Если функция имеет z-преобразование и если существует предел
![]() ,
,
то
![]() (4.108)
(4.108)
Из
теоремы следует, что значение дискретного
сигнала
![]() при t
= 0
определяется
значением
при
при t
= 0
определяется
значением
при
![]() .
.
Д о к а з а т е л ь с т в о. По определению можно представить в виде

Возьмем предел от каждой части последнего выражения и, учитывая, что z стремится к бесконечности, получим
![]() (4.109)
(4.109)
6.
Теорема
о конечном значении.
Если функция
имеет z-преобразование
и
функция
![]() не имеет полюсов на окружности
единичного радиуса
не имеет полюсов на окружности
единичного радиуса
![]() или вне ее на z-плоскости,
то
или вне ее на z-плоскости,
то
![]() (4.110)
(4.110)
Д о к а з а т е л ь с т в о. Рассмотрим два ряда с конечным числом членов:
 (4.111)
(4.111)
 (4.112)
(4.112)
Предположим,
что
=
0 при t
< 0,
тогда
в
выражении (4.112)
![]() .
Сравнивая выражения (4.111)
и (4.112), видим, что последний
ряд может быть записан как
.
Сравнивая выражения (4.111)
и (4.112), видим, что последний
ряд может быть записан как
 (4.113)
(4.113)
Определим
в
пределе при
![]() разность между выражениями (4.111) и
(4.113):
разность между выражениями (4.111) и
(4.113):
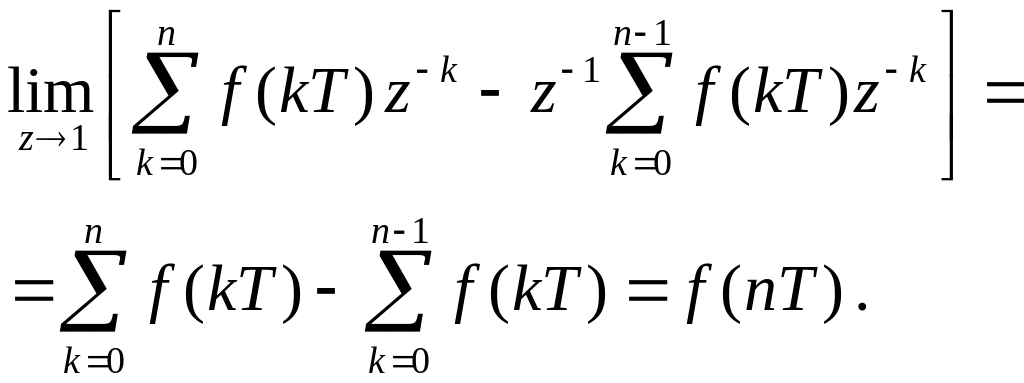 (4.114)
(4.114)
В
последнем выражении возьмем предел при
![]() ,
тогда
,
тогда
 (4.115)
(4.115)
Меняя порядок перехода к пределу в последнем выражении и учитывая, что

получим
![]()
что и является доказательством теоремы о конечном значении.
Пример 4.3. Используя теорему о конечном значении, определить конечное значение f(kT) для заданного z-преобразования

Для решения нужно применить теорему о конечном значении, так как функция

не имеет полюсов на единичной окружности |z| = 1 или вне ее. Следовательно, получим

Полученный
результат можно проверить разложением
F(z)
в
ряд по степеням
![]() :
:

Видно, что последовательность значений коэффициентов ряда быстро сходится к установившемуся значению, равному единице.
7. Теорема дифференцирования. Пусть z-преобразование функции f(t, а) есть F(z, а), где а независимая переменная или константа. Тогда z-преобразование частной производной функции f(t, а) по а определяем как
 (4.116)
(4.116)
Д о к а з а т е л ь с т в о. По определению

Теорема о свертке во временной области. Если функции
 и
и
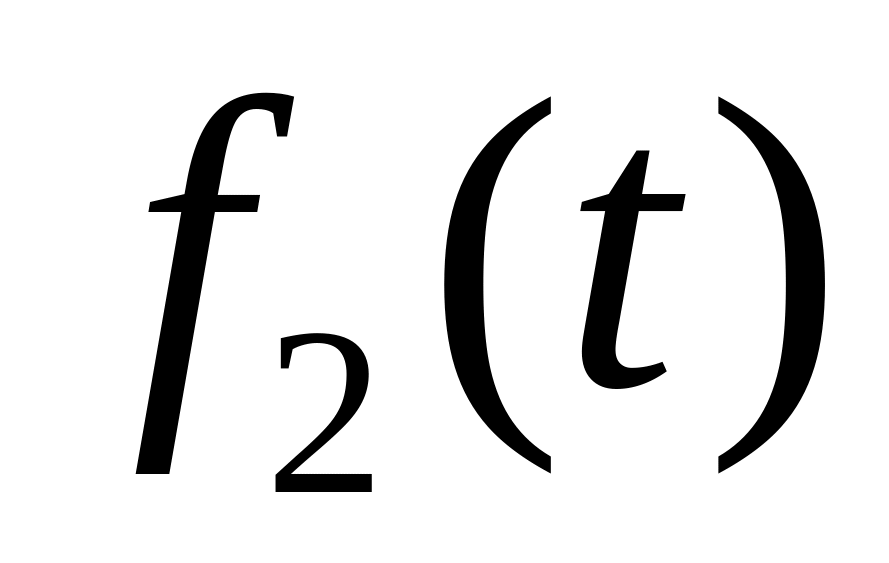 имеют
z-преобразования
F1(z)
и F2(z)
соответственно и
имеют
z-преобразования
F1(z)
и F2(z)
соответственно и
 для t
< 0,
то
для t
< 0,
то
 (4.117)
(4.117)
Д о к а з а т е л ь с т в о. Правая часть уравнения (4.117) может быть записана в виде
 (4.118)
(4.118)
Полагая
![]() и
изменяя порядок суммирования, получим
и
изменяя порядок суммирования, получим
 (4.119)
(4.119)
Так
как
![]() для t<
0,
то последнее выражение примет вид
для t<
0,
то последнее выражение примет вид
 (4.120)
(4.120)
Нетрудно заметить, что теорема о свертке во временной области аналогична соответствующей теореме преобразования Лапласа. Однако необходимо помнить, что обратное z-преобразование (или Лапласа) произведения двух функций не равно произведению соответствующих оригиналов, т. е.
![]() (4.121)
(4.121)
9.
Теорема о свертке в области изображений.
Если z-преобразования
и
соответственно равны
![]()
![]() ,
то z-преобразование
произведения
этих двух функций
,
то z-преобразование
произведения
этих двух функций
 (4.122)
(4.122)
где Г окружность, которая лежит в кольцевой области, определяемой выражениями:

где
![]() и
и
![]()
радиусы сходимости соответственно
радиусы сходимости соответственно
![]() и
и
![]() .
.
