4.5.2. Обратное z-преобразование

Преобразование Лапласа и его обратное преобразование являются однозначными, т. е. если есть преобразование Лапласа для функции , то является обратным преобразованием Лапласа для функции . Для z-преобразования обратное z-преобразование не является однозначным. Z-преобразование определяется функцией , а обратное z-преобразование не обязательно равно . Корректный результат обратного z-преобразования функции есть , который равен только в моменты квантования .

На рис. 4.13 проиллюстрирован тот факт, что для z-преобразования единичной ступенчатой функции, которое равно и соответствует последова­тельности единичных импульсов, обратное z-преобразование может быть любой функцией, значения которой равны единице в моменты . Неоднозначность обратного z-преобразования является одним из ограничений, о котором необходимо помнить при применении аппарата z-преобразования.

Обратное z-преобразование обозначают как

(4.73)

В общем случае обратное z-преобразование может быть определено одним из следующих трех методов.

Метод разложения на простые дроби. Этот метод при небольшой модификации соответствует методу разложения на простые дроби в пре­образовании Лапласа. При анализе непрерывных систем обратное преобра­зование Лапласа функции может быть получено разложением в виде

(4.74)

где и с  отрицательные полюса (здесь предполагается случай простых полюсов); А, В и С − вычеты в этих полюсах. Тогда обрат­ное преобразование Лапласа функции определяется как

(4.75)

Для случая z-отображения не надо представлять в форме (4.74).

Рис. 4.13. Неоднозначность обратного z-преобразования­

Дело в том, что в таблице z-преобразований обратное z-преобразование для выражения вида отсутствует, хотя при положительном значении а член такого вида соответствует последовательности импульсов с экспоненциально затухающей амплитудой, когда присутствует временная задержка. Вместе с тем известно, что обратное z-преобразование функции равно . Следовательно, удобнее разложить на простые дроби функцию . После разложения обе части выражения для умножают на z для получения .

Для функций, которые не содержат нулей (z = 0), соответствующая последовательность импульсов имеет временной сдвиг. Разложение функ­ции на простые дроби представляется в обычном виде, т. е.

(4.76)

После чего находим

(4.77)

Если найдено обратное z-преобразование функции , то обратное z-преобразование функции определяется следующим образом:

(4.78)

Равенство в выражении (4.78) является прямым результатом соотноше­ния (4.65), если для всех k < 0.

Рассмотрим применение этого метода для

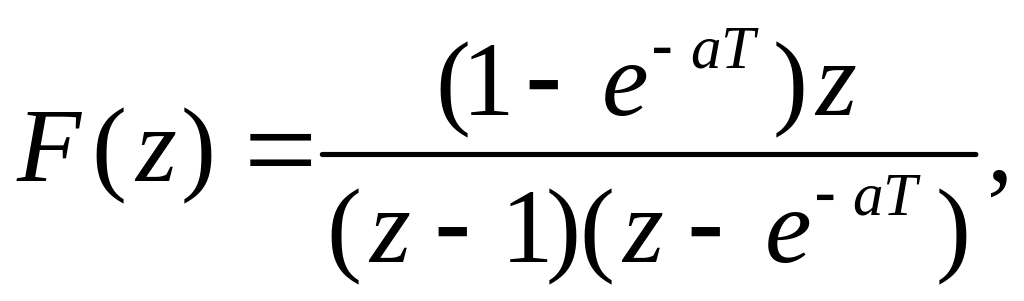
где а  положительное постоянное число; Т  период квантования.

Используя ме­тод разложения на простые дроби, найти обратное z-преобразование , .

Разложение на простые дроби дает

Следовательно, получаем:

Из таблицы z-преобразований (п 2)может быть найдено обратное z-преобразование в виде временной функции, значения которой в моменты квантования определяются как

Следовательно, дискретная временная функция может быть записана в виде

Заметим, что временная функция не может быть найдена из обратного z-преобразования, так как оно не определяет значения функции между моментами замыкания.

Метод разложения в степенной ряд. Из выражения (4.65) следует, что обратное z-преобразование функции может быть определено разложением ее в бесконечный ряд по степеням . Из выражения (4.65) получаем:

(4.79)

Следовательно, коэффициенты ряда соответствуют значениям в мо­менты квантования. Основное различие между методами разложения на простые дроби и в степенной ряд заключается в том, что первый метод дает решение для в компактной форме, в то время как решением второго метода является последовательность чисел. Разумеется, оба ме­тода эквивалентны, и для последовательности чисел также может быть записано выражение в компактной форме.

Рассмотрим пример обратного z-преобразования функции

Последовательное деление числителя на знаменатель дает

В этом случае легко видеть, что

и, следовательно,

Это совпадает с результатом, полученным методом разложения на простые дроби.

Метод, основанный на использовании формулы обращения. Интересно сравнить определения преобразования Лапласа и z-преобразования. Если для функции аргумента t существует преобразование Лапласа, то это преобразование Лапласа и z-преобразование функции соот­ветственно равны:

Обратное преобразование Лапласа определяем как

где с  абсцисса сходимости, которую выбираем таким образом, чтобы особые точки подынтегральной функции лежали слева от нее. Можно показать, что для обратного z-преобразования существует аналогичное выражение

(4.80)

где Г – замкнутый контур (обычно окружность) на z-плоскости, включающий все особые точки .

Подставляя в выражение для обратного преобразования Лапласа получим

. (4.81)

Как показано на рис. 4.14, а, интеграл (4.81) берется вдоль прямой линии , проходящей от до . Эта прямая пересекает периодические полосы на s-плоскости, и, следовательно, интеграл (4.81) может быть представлен в виде суммы интегралов, каждый из которых берется в пределах одной периодической полосы. Тогда

(4.82)

где . Заменяя р на , где  целое число, получим выражение (4.82) в виде

(4.83)

или

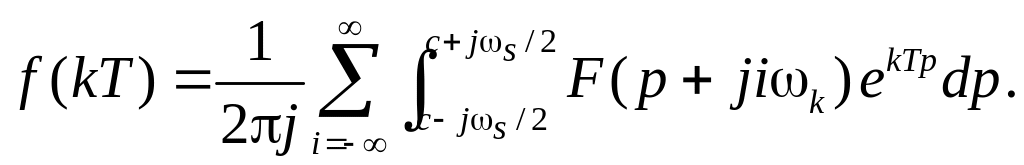(4.84)

Рис. 4.14. Контуры интегрирования на s- и z-плоскостях

при использовании формулы обращения

Меняя порядок суммирования и интегрирования в последнем выражении, получим

(4.85)

Так как из выражения (4.55) следует, что

(4.86)

то уравнение (4.85) можно представить как

(4.87)

Подставляя в (4.87) и учитывая, что

(4.88)

(4.89)

(4.90)

Получим

(4.91)

Линия интегрирования от до отображается в окружность на z-плоскости (рис. 4.15, б). Так как на р-плоскости не имеет особых точек на линии интегрирования , или справа от нее, то все особые точки должны лежать на z-плоскости внутри окружности Г, .