4.12.3. Критерий абсолютной устойчивости

Обозначим

(4.328)

В отличие от временной характеристики g((k  s)T), равной нулю при k < s, т. е. при отрицательных значениях аргумента, g((k  s)T), как видно из (4.328), существует как при положительных, так и при отрицательных значениях аргумента. Причем

(4.329)

Пользуясь (4.328), можно квадратичную форму (4.323) представить в виде

(4.330)

Установим, прежде всего, условия неотрицательности квадратичной формы (4.330). Для этой цели воспользуемся двусторонним преобразованием Фурье:

(4.331)

Обратное преобразование

(4.332)

определяет по спектральной функции . Подставляя из (4.332) в (4.330), после перемены порядка суммирования и интегрирования получим

(4.333)

Или так как

(4.334)

то

(4.335)

Отсюда видно, что условие неотрицательности [ см. неравенство (4.312)] будет выполнено при любой , если будет неотри­цательна спектральная функция , т. е. если

(4.336)

Но из (4.331) при учете (4.328) следует

(4.337)

Замечая, что

(4.338)

получим

(4.339)

или

(4.340)

где  частотная характеристика линейной импульсной части. Таким образом, условие неотрицательности [см. неравенство (4.336)] запишется в виде

(4.341)

Это же неравенство является также условием неотрицательности и [см. неравенство (4.326)].

Геометрический смысл неравенства (4.341) весьма прост. Проведем на плоскости частотной характеристики W* вертикальную прямую через точку (рис. 4.34).

Рис. 4.34. Частотная характеристика системы

Тогда неравенство (4.341) будет выполнено, если частотная характеристика линейной части импульсной системы будет расположена справа от вертикальной прямой.

Теперь можно перейти к формулировке критериев устойчивости состояния равновесия и процессов. Для этого достаточно использовать условие (4.341) и выяснить конкретный смысл функции S(x^c, k). При рассмотрении устойчивости состояния равновесия, как видно из (4.327), S(x^c, k) представляет собой статическую линеаризацию нелинейного элемента, т. е.

(4.342)

Поэтому критерий устойчивости состояния равновесия нелинейной импульсной системы можно сформулировать следующим образом.

Состояние равновесия нелинейной импульсной системы с устойчивой линейной частью будет абсолютно устойчивым, если коэффициент статической линеаризации нелинейного элемента удовлетворяет неравенству

(4.343)

а частотная характеристика линейной импульсной части расположена справа от вертикальной прямой , где r > r₀.

Условие, налагаемое на коэффициент статической линеариза­ции (4.343), равносильно условию принадлежности характеристики нелинейного элемента Ф(x) сектору (0, r) (рис. 4.35).

y=Ф(x)

rx

x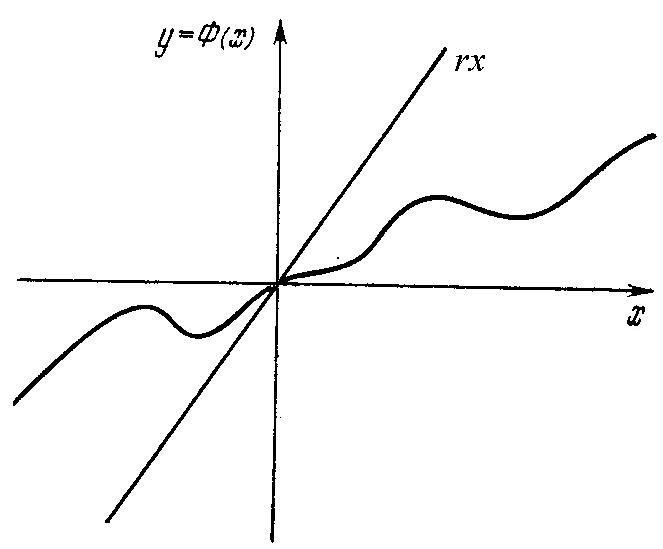

Рис. 4.35. Сектор принадлежности характеристики нелинейного звена

При рассмотрении устойчивости процессов, как следует из (4.298) и (4.303),

(4.344)

т. е. S(x^c, k) представляет собой разделенную разность. Для непрерывной и дифференцируемой характеристики нелинейного элемента неравенство

(4.345)

равносильно неравенству

(4.346)

т. е. неравенству относительно коэффициента дифференциальной линеаризации . Поэтому критерий устойчиво­сти процессов можно сформулировать следующим образом.

Процессы в нелинейной импульсной системе с устойчивой импульсной частью, вызываемые ограниченным внешним воздействием, будут устойчивыми, если коэффициент дифференциальной линеаризации нелинейного элемента удо­влетворяет условию

(4.347)

а частотная характеристика линейной импульсной части расположена справа от вертикальной прямой , где r > r₀.

Условие (4.347), налагаемое на коэффициент дифференциальной линеаризации , равносильно не только условию принадлежности характеристики нелинейного элемента сектору (0, r), но и ее монотонности (рис. 4.36).

y=Ф(x)

rx

x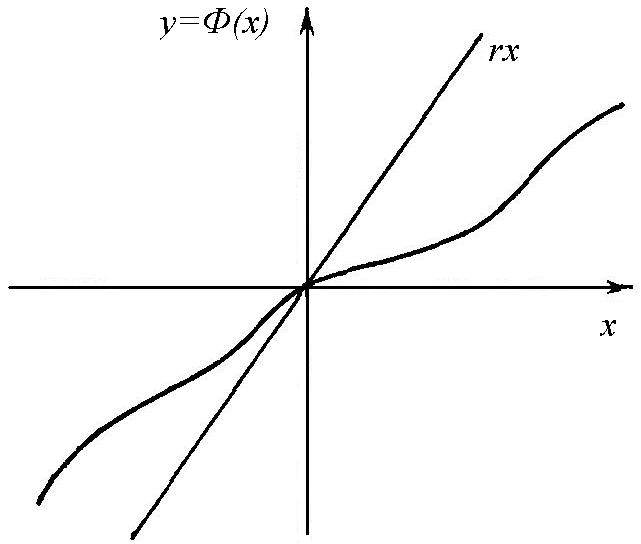

Рис. 4.36. Монотонность нелинейной характеристики

Критерий абсолютной устойчивости процессов предъявляет более жесткие требования к характеристике нелинейного элемента, чем критерий абсолютной устойчивости состояния равновесия.

Если характеристика нелинейного элемента зависит от времени:

y = Ф(х, k), то и коэффициенты статической линеаризации

(4.348)

и дифференциальной линеаризации

(4.349)

будут также зависеть от времени k. Критерии абсолютной устойчивости состояния равновесия и процессов такой нестационарной системы формулируются так же, как и выше, но вместо стационарных коэффициентов статической и дифференциальной линеаризации в них фигурируют нестационарные коэффициенты статической и дифференциальной линеаризации и условия вида (4.349), (4.347) должны выполняться при всех значениях k.