4.8.4. Переходные уравнения состояния цифровых стационарных систем

Если линейная цифровая система стационарна, ее уравнения динамики можно записать в нескольких видах:

(4.196)

(4.197)

где  переходная матрица состояния;

(4.198)

(4.199)

или

(4.200)

(4.201)

или

(4.202)

Как было показано выше, матрицы Ф(Т) и Ф(1) всегда невырождены, если элементы А конечны. Однако в общем случае не существует ограничений на матрицы коэффициентов чисто цифрового уравнения состояния, так что А может быть вырожденной матрицей.

Как и для нестационарных систем, стационарное уравнение состояния можно решить с помощью итерационной процедуры. Для уравнения (4.202) решение имеет вид

(4.203)

где

(4.204)

Следует заметить, что Ф(NT)  это только обозначение, используемое для упрощения записи в выражении (4.204). В общем случае Ф(NT) не равно Ф(Т), где Т заменено на NT, хотя в простейших случаях равенство может оказаться справедливым.

Для уравнения (4.201) переходное уравнение состояния имеет вид

(4.205)

Эти переходные уравнения состояния можно записать также со сдвигом для нулевого начального времени или шага, т. е.

(4.206)

или

(4.207)

Дискретные уравнения состояния можно получить также в результате приближенного описания аналоговой системы цифровой моделью. Рассмотрим следующие уравнения динамики аналоговой системы:

(4.208)

(4.209)

Перейдем к цифровой аппроксимации системы в моменты t = t_k.

Положим

(4.210)

Производную от x(t) в момент t = t_k можно приблизительно вычислить с помощью следующего соотношения:

(4.211)

Затем уравнение (4.208) аппроксимируем выражением

(4.212)

По аналогии уравнение (4.209) принимает вид

(4.213)

Уравнение (4.212) окончательно запишем в форме дискретного уравнения состояния

(4.214)

Связь уравнения состояния с передаточной функцией

Представляет интерес исследовать взаимосвязь метода переменных состояния и метода, основанного на понятии передаточной функции.

Предположим, что цифровая многомерная система описана с помощью z-преобразования соотношением

, (4.215)

где

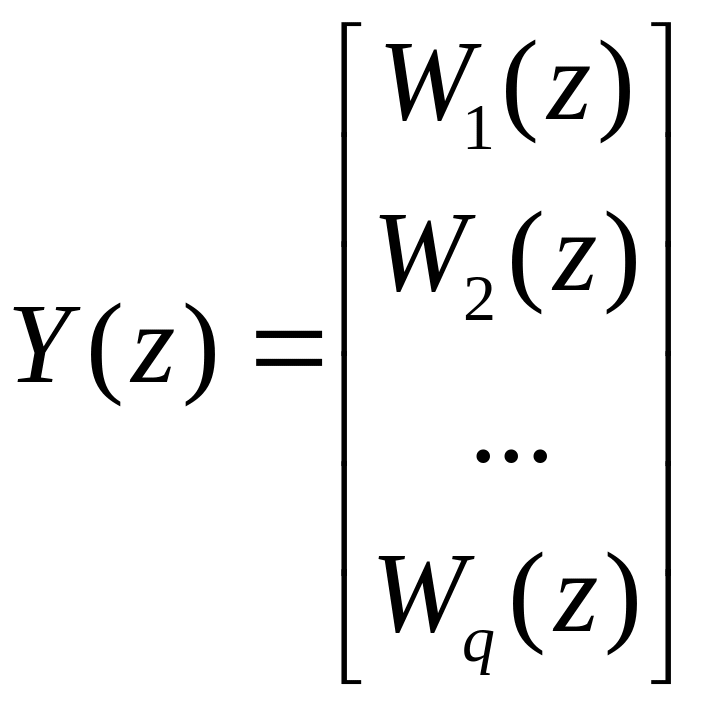(4.216)

есть z-преобразование (q  1)-мерного вектора выхода;

(4.217)

есть z-преобразование (р1)-мерного вектора входа;

(4.218)

есть матричная дискретная передаточная функция размерностью q  р.

Элементы матрицы W(z) имеют вид

(4.219)

Теперь опишем цифровую систему уравнением динамики:

(4.220)

(4.221)

Вычисляя z-преобразование от обеих частей выражения (4.220) и разрешая его относительно X(z), получим

(4.222)

Подстановка (4.222) в z-преобразование от выражения (4.221) дает

(4.223)

Передаточная функция определяется при нулевом начальном состоянии х(0), поэтому выражение (4.223) упрощается до

(4.224)

Из сравнения выражений (4.223) и (4.224) видно, что матричная дискретная передаточная функция системы может быть записана в виде

(4.225)

Если в дискретной системе имеются операции выборки-хранения в выражении (4.225), нужно лишь заменить матрицы А и В на Ф(Т) и Ө(Т) соответственно. Конечно, это можно сделать только при условии, что для системы существует дискретная передаточная функция.

Обратное преобразование матричной передаточной функции называется импульсной переходной матрицей. Применив обратное z-преобразование к обеим частям формулы (4.225), получим

(4.226)

где (0)  дельта-функция при t = 0.

Поскольку [(k1)T] = 0 для k < 1, матрицу g(kT) можно записать в виде

(4.227)

(4.228)

В качестве иллюстрации рассмотрим случай, когда требуется определить передаточную функцию разомкнутой системы:

Подставляя найденные значения в формулу (4.225), получаем передаточную функцию системы

Чтобы использовать метод z-преобразования необходимо вначале определить передаточную функцию линейного процесса. На основании уравнений динамики процесса запишем дифференциальное уравнение, связывающее u(t) и c(t):

где u(t)  выходной сигнал экстраполятора нулевого порядка. Отсюда передаточная функция

С учетом приведеных схем дискретная передаточная функция всей системы

или

Вычисляя z-преобразование, имеем

что совпадает с полученным выше результатом.

Импульсную весовую последовательность систем можно найти обратным z-преобразованием W(z). Разложение W(z) на элементарные слагаемые дает

Отсюда

для k > 0. Для k = 0 g(0) = 0.

Другой метод определения g(k) основан на использовании формул (4.227) и (4.228). В этом случае

для k >0.

Переход от модели непрерывной системы с запаздыванием к дискретной модели. Пусть непрерывная система описывается уравнением

(4.229)

Первый вариант:

Пусть время запаздывания  меньше периода квантования Т.

Интегрирование (4.229) в пределах одного периода квантования есть

(4.230)

Так как сигнал u(t) в дискретном варианте модели постоянен в течение периода квантования, то сигнал u(t – ) будет кусочно-постоянен. В соответствии с изменением управляющего сигнала u(t – ) в течении одного периода квантования удобно разбить интервал интегрирования на две части так, чтобы u(t – ) был постоянен в обеих частях. Тогда интеграл из уравнения (4.230) перепишем

Таким образом, в результате квантования непрерывной системы получаем

(4.231)

где ;

(4.232)

(4.233)

Модель в терминах уравнения состояния имеет вид

(4.234)

Второй вариант. Пусть время запаздывания  больше Т. Если , , где d – целое число, то можно вывести следующее уравнение:

(4.235)

где Г₀ и Г₁ находят из уравнений (4.232) и (4.233) с заменой  на ₁. Описание в пространстве состояний имеет вид

(4.236)

Переход от разностного уравнения к модели в переменных состояниях. Пусть разностное уравнение получено на основе дискретной передаточной функции

(4.237)

и имеет вид

(4.238)

Введем следующие переменные состояния:

(4.239)

(4.240)

Используя соотношения (4.240), запишем модель в переменных состояниях в виде

(4.241)

и уравнение выхода

(4.242)

С учетом исходной передаточной функции можно записать

(4.243)

Теперь пусть имеем более полную передаточную функцию

(4.244)

С учетом (4.243) перепишем уравнение (4.244) в виде

или

(4.245)

Используя уравнение (4.240), можно переписать (4.245) в виде

(4.246)

и, подставляя из системы уравнений (4.241), получаем

(4.247)

В матричной форме уравнение (4.247) запишем в виде

(4.248)

Наконец, рассмотрим модель в переменных состояниях со скалярным управлением с задержкой на входе на d тактов:

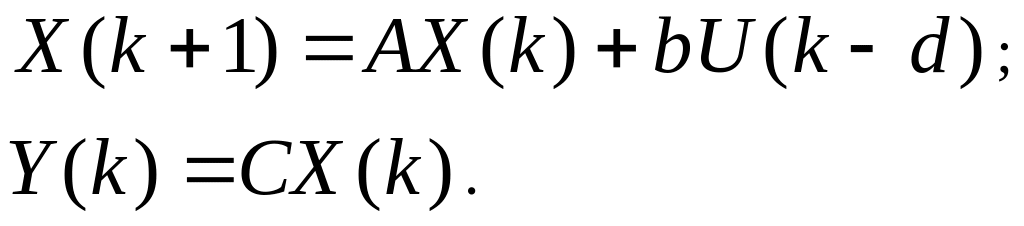(4.249)

Запаздывание можно представить в виде совокупности d единичных задержек, помещаемых на входе системы (рис. 4.22).

Рис. 4.22. Структурная схема объекта управления

с задержкой входного сигнала

Звенья, которые формируют задержку сигнала в соответствии со структурой (рис. 4.22), могут быть описаны в пространстве состояния:

, (4.250)

, (4.251)

где

Объединив уравнения (4.249), (4.250) и (4.251), получим расширенную систему

(4.252)