Глава 4. Анализ дискретных систем автоматического управления
4.1. Свойства дискретных систем
В предыдущих главах использовалось предположение о том, что математическая модель системы управления позволяет с той или иной точностью предсказывать состояние ее характеристик в любой момент времени.
Во многих практических ситуациях, а особенно при управлении сложными объектами, это предположение не оправдано.
Более слабым условием может быть предсказание состояния системы в некоторые моменты времени t = tk, k = 0, 1, 2, …, образующие дискретную последовательность. Состояние системы в любые промежуточные моменты времени не определено. Кроме того, любая текущая информация, поступающая в течение работы системы, также может характеризовать ее состояние только в те же моменты времени tk. Процесс преобразования непрерывных сигналов в дискретные кванты – называется квантованием. Кроме квантования сигналов по времени существуют системы, в которых квантуются сигналы и по уровню. В качестве примера можно привести компьютерную систему управления (рис. 4.1).
Рис. 4.1. Цифровая система управления
Микропроцессорный компьютер в этой системе выполняет функцию управляющего устройства (регулятора). Входным интерфейсом компьютера является цифро-аналоговый преобразователь (ЦАП), который преобразует двоичный код, формируемый компьютером, в напряжение, для воздействия на объект управления. Компьютер, который работает в реальном времени, может принимать сигналы и выполнять определенные расчеты только в дискретные моменты времени. Пусть эти моменты отстоят друг от друга на постоянную величину, которую можно назвать периодом квантования. Если скорость обработки информации в компьютере высокая, то результаты обработки будут задерживаться на небольшое число периодов квантования. Входной интерфейс (АЦП) достаточно часто выполняет также квантование входных сигналов по уровню.
Начало использования дискретных систем регулирования относится к началу промышленной революции. Управление паровой машиной осуществлялось за такт впуска пара. Такое регулирование получило название регулирование с отсечкой пара. При ручном регулировании инерционных объектов было замечено, что процесс управления упрощается, если перемещение регулирующего органа осуществлять импульсами, а в паузах наблюдать за результатом действия импульсов.
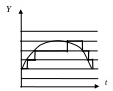
В 30-х гг. прошлого столетия импульсное управление позволило получать огромные коэффициенты усиления по мощности (до 1014). В 40-е гг. начинает формироваться теория импульсного управления. На рис. 4.2 показаны примеры квантования функции y.
Рис.4.2. Квантование функции y: а по времени; б − по уровню; в − по уровню и по времени одновременно
При квантовании по уровню сигнал формируется, когда функция переходит через один из уровней квантования. При одновременном квантовании по уровню и по времени значения функции фиксируются в равноотстающие моменты времени и округляются до ближайшего уровня.
Дискретные системы, соответствующие каждому из способов квантования, получили наименование импульсных, релейных и цифровых систем автоматического управления. При формировании дискретных сигналов из непрерывных осуществляется их модуляция.
Если ширина импульсов и их период повторения остаются неизменными, а амплитуда меняется в функции входного непрерывного сигнала, то такая модуляция называется амплитудно-импульсной модуляцией. Если высота импульсов и их период повторения остаются неизменными, а ширина импульсов меняется в функции амплитуды непрерывного сигнала, то имеем широтно-импульсную модуляцию.
Для класса специальных систем управления используется времяимпульсная модуляция, которая подразделяется на частотно-импульсную и фазоимпульсную модуляции. При частотно-импульсной модуляции меняется частота импульсов в зависимости от амплитуды непрерывного сигнала. При фазоимпульсной модуляции меняется фаза импульсов относительно непрерывного входного сигнала.
В промышленных системах автоматизации используются первые два метода модуляции, причем широтно-импульсная модуляция в основном применяется для управления энергией питания электродвигателей и электронагревательных элементов. Из всех видов модуляции только амплитудно-импульсная модуляция сохраняет условия принципа суперпозиции, т. е. линейности преобразований сигналов. Все другие способы модуляции нарушают этот принцип.