2.5 Исполнительные механизмы

по виду энергии для питания данных устройств применяются:

1. электрические исполнительные механизмы;

2. пневматические исполнительные механизмы.

1. Электромагнитные исполнительные механизмы

По виду питающего напряжения бывают:

1. электромагнитные исполнительные механизмы переменного тока;

2. электромагнитные исполнительные механизмы постоянного тока.

По величине перемещения исполнительной части:

1. короткоходовые (рис1);

2. длинноходовые (рис2).

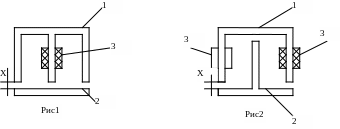
1 – сердечник, на котором - катушка 3; 2 – якорь (подвижная часть).

Принцип действия:

При подаче напряжения в катушку возникает магнитодвижущая сила, которая создает тяговое усилие между 2 и 1. Следовательно якорь притягивается к сердечнику. Величина тягового усилия определяется по формуле:

,

где I – ток в катушке

W – число витков

G – магнитная проводимость в зазоре между 2 и 1

Х – расстояние между 2 и 1.

Для короткоходовых (рис1) х =3 5мм.

Для рис 2 х =50 150мм.

2. Электродвигательные исполнительные механизмы

W1, w2 – обмотки двигателя.

С – фазодвигающий конденсатор

- ротор двигателя

- механические связи.

Угол поворота ротора 0 - 120 .

Для контроля угла поворота применяются конечные выключатели S1 и S2. на эти выключатели воздействует кулачек К, который поворачивается вместе с валом ротора. С валом ротора связан редуктор R и РО.

Для изменения направления поворота ротора применяется переключатель 1. для сокращения времени свободного выбега вала ротора при отключении питания применяется R1 и R2.

Вал ротора связан со стрелкой реостата обратной связи Rос. При вращении ротора перемещается стрелка относительно центра данного реостата. При этом в цепи между средней точкой и положением стрелки возникает ток, пропорциональный величине перемещения данной стрелки.

Данный ток измеряется амперметром. Его величина описывает положение вала ротора данного электродвигателя. Поэтому данный амперметр называется измерителем положения вала ротора И.М.

Основные характеристики:

1. Максимальный момент на валу двигателя (Мmax)

2. время поворота ротора двигателя на максимальный угол (Тmax). По характеристикам можно описать данный ИМ

~ КПД э/двигателя.

2.5.3 Пневматические исполнительные механизмы

Устройство автоматической системы управления или регули­рования, воздействующее на процесс в соответствии с получае­мой командной информацией, называется исполнительным устройством. Оно предназначено для изменения притока или расхода вещества либо энергии и приближения регулируе­мой величины к заданному значению. Исполнительные устройства состоят из пневматиче­ского, электрического или гидравлического исполнительного ме­ханизма и регулирующего органа. В химической промышлен­ности в автоматических системах часто используют пневматиче­ские мембранный и поршневой исполнительные механизмы, а в качестве регулирующих органов – регулирующий клапан и за­слонку.

Наибольшее распространение получил пневматический мембранный исполнительный механизм (рис. III-19, а), выполненный из прорезиненной мембраны, зажатой между двумя крышками так, что в верхней части образуется герметически закрытая полость. Снизу через жесткий центр, связанный со штоком, мембрана опирается на пружину. Сжа­тый воздух от автоматического регулятора направляется в верх­нюю полость над мембраной и перемещает ее вместе со штоком вниз. При этом пружина сжимается и уравновешивает усилие, действующее на мембрану сверху. Перемещение штока переда­ется на регулирующий орган. В отличие от мембранного, в порш­невом пневматическом исполнительном механизме (рис. III. 19,б) сжатый воздух от регулятора подается в цилиндр и перемещает поршень со штоком и регулирующий орган.

Схемы регулирующих органов показаны на рис. III-20. В ре­гулирующем клапане шток исполнительного механизма жестко связан с затвором (рис. 111-20, а). При перемещении последнего относительно седла изменяется проходное сечение и соответст­венно расход вещества, проходящего через регулирующий орган. В заслоночном регулирующем органе (рис. Ш-20, б) шток при­вода через рычаг, соединенный с осью, вращает заслонку, ко­торая изменяет расход вещества.

Исполнительное устройство, состоящее из пневматического мембранного исполнительного механизма и регулирующего ор­гана, называют пневматическим регулирующим клапаном (рис. III-21).

По виду запорпого устройства пары затвор – седло пневмати­ческие регулирующие клапаны делят на односедельные и двухседельные. Первые имеют неуравновешенный затвор, так как на него действует выталкивающая сила среды, и поэто­му применяются в исполнительных устройствах малых размеров при низких давлениях среды. Вторые имеют уравновешенный затвор и используются в исполнительных устройствах больших размеров и при высоких давлениях среды.

Рис. III.19. Схемы мембранного (а) и поршневого (б) исполнительных ме­ханизмов: 1- шток; 2 — пружина; 3 — мембрана; 4 — поршень.

Рис. Ш-20. Схемы регулирующих органов:

о - одкоседельного; б— заслоночного; 1 — корпус; 2 — затвор; 3 — шток; 4 — заслонка.

Рис. Ш-21. Схемы пневматических регулирующих клапанов:

а — нормально открытого (НО): б – нормально закрытого (НЗ); 1 – корпус; 2 – затвор; 3 — шток; 4 — пружина; 5—мембрана.

При расчете АСР пневматический регулирующий клапан представляют апериодическим звеном 1-го порядка.

Динамическая характеристика где Т-время зависит от жесткости, Q-величина потока K-величина усиления, Р - давления воздуха.

3 Основы теории автоматического регулирования

3.1 Способы математического описания АСР

Динамические характеристики элементов АСР описываются 2-мя способами: 1) Дифференциальные уравнения 2) Передаточные функции

3.1.1Дифференциальные уравнения (обыкновенные)

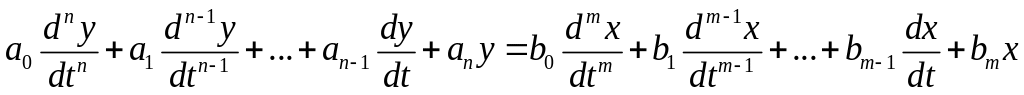
у - выходная переменная АСР, х - входная, dt - динамика АСР. Для решения уравнения применяют операционное исчисление основанные на преобразовании Лапласа.

3.1.2 Передаточные функции

Преобразование Лапласа имеет следующий вид

гдн - аргумент, - изображение данного аргумента , - некоторая переменная которая называется переменная Лапласа

Свойства преобразования при начальных нулевых значениях т.е. t=0 x(t)=0

1) , , 2) , 3) , , 4) , где L-преобразование

Преобразование по Лапласу с использованием его свойств

возьмем отношение

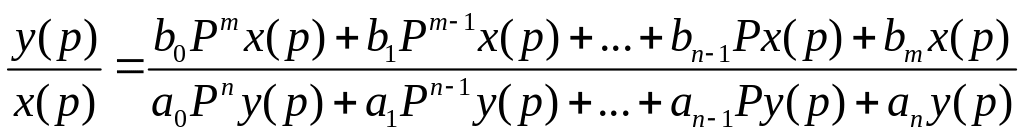
Отношение преобразуем по Лапласу выходной величины АСР или линейно к преобразованной по Лапласу входной величины элемента называется передаточной функцией АСР или элемента. Знаменатель передаточной функции = 0, называется характеристическим уравнением АСР