39. Дифференциальные уравнения высших порядков. Задача Коши. Геометрический и механический смысл.

40. Дифференциальные уравнения, допускающие понижение порядка.

Дифференциальные уравнения второго порядка

Рассмотрим дифференциальное уравнение второго порядка, разрешенное относительно старшей производной y^// = f(x,y,y^/).

Общее решение y = j(x,C₁,C₂), (2.2),где С₁,С₂ - независимые постоянные, и тогда (2.2) представляет собой бесконечную совокупность интегральных кривых. Вообще через каждую точку М₀(х₀,у₀) плоскости О_ху проходит пучок интегральных кривых. Поэтому нужно не только выбрать кривую, но еще и указать ее направление.Случаи понижения порядка

Дано уравнение второго порядка у^// = f(x,y,y^/). (2.7)

1. Пусть левая часть не содержит х, то есть у^// = f(y,y^/).Тогда положим у^/ = р, .

Таким образом получим дифференциальное уравнение первого порядка .

2. Пусть левая часть не содержит у, то есть у^// = f(х,y^/).Тогда положим у^/ = р, , и снова получим уравнение первого порядка

41. Линейная независимость функций. Определитель Вронского.

Определителем Вронского W(x; y₁(x), y₂(x), ..., y_n(x)) называется определитель, первая строка которого образована функциями y₁(x), y₂(x), ..., y_n(x) из C_n-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:

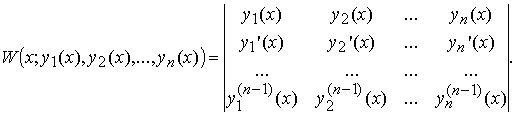
Справедливо следующее необходимое условие линейной зависимости функций.

Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y₁(x), y₂(x), ..., y_n(x)) ≡ 0 на [a;b].

Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке.

 Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Рассмотрим две функции:

Эти функции линейно независимы на [0, 2]. Действительно:

Вычислим определитель Вронского W(x; y₁(x), y₂(x)) на [0, 2]: 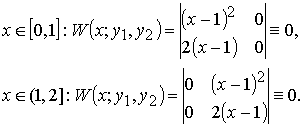Итак, функции линейно независимы на [0, 2], а W(x; y₁(x), y₂(x)) ≡ 0 на [0, 2].

Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций.

С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций.

(Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём).

Определителем Вронского вектор-функций Y₁(x), Y₂(x), ..., Y_n(x), 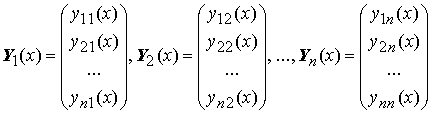называется определитель W[x; Y₁, Y₂, ..., Y_n], заданный равенством

 

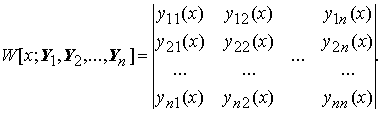
42. Линейные однородные дифференциальные уравнения. Общее решение.Линейным дифференциальным уравнением называется уравнение вида y⁽ⁿ⁾ + f_n-1(x)y^{(n - 1)} + ... + f₁(x)y' + f₀(x)y = 0.Общее решение линейного однородного дифференциального уравнения (*)с непрерывными на интервале интегрирования X коэффициентами определяется линейной комбинацией , где - линейно независимые частные решения ЛОДУ на X, а - произвольные постоянные. Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид y₀ = C₁ ⋅ y₁ + C₂ ⋅ y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные.

43. Решение линейных однородных дифференциальных уравнений с постоянными коэффициентами. Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами .

1)Записываем характеристическое уравнение k² + p ⋅ k + q = 0.

2)Находим корни характеристического уравнения k₁ и k₂.

3)В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде

, если ;

, если ;

, если .