Зависимость константы скорости реакции от температуры Рассмотрим химическую реакцию

aA + bB = cC + dD

Скорость этой реакции

2.7

где k - константа скорости, независящая от концентрации реагирующих веществ

C_A, C_B - концентрации реагирующих веществ

a, b -стехиометрические коэффициенты

Концентрации реагирующих веществ либо слабо зависят от температуры, либо совсем не зависят. Температура же оказывает на скорость химической реакции более сильное влияние, чем концентрации реагирующих веществ.

Исторически известны два вида зависимости константы скорости реакции от температуры:

1. эмпирическое правило Вант-Гоффа

2. и более строгое – это уравнение Аррениуса.

Рассмотрим правило Вант-Гоффа.

В области умеренных температур для гомогенных и многих гетерогенных реакций увеличение температуры на 10^оС (или К) при постоянных концентрациях реагирующих веществ приводит к возрастанию скорости реакции в 2 – 4 раза.

С учетом постоянства концентраций реагирующих веществ следуют следующие соотношения скоростей реакции, констант скоростей реакций и времени протекания этих реакций

2.8

Если T=10n, где n - целое число, то правило Вант-Гоффа запишется в виде

2.9

принимая T₂ =T + 10n, T₁ =T (T₂ >T₁) из 2.9 получаем следующее выражение

2.10

Величина γ = 2 - 4, постоянная для данного химического процесса, называется коэффициентом Вант-Гоффа или температурным коэффициентом скорости реакции. Из выражения (2.9) следует, что скорость реакции возрастает тем сильнее, чем больше ее коэффициент Вант-Гоффа и нагрев реакционной среды.

При γ = 2 увеличение температуры на 100 К ведет к росту скорости реакции в 2¹⁰= 1024 раза, при γ =3 в 3¹⁰ = 59049 раз.

Пример 2.1

При 100⁰С реакция заканчивается за 40 сек. За какое время завершится та же реакция при 20⁰С, если температурный коэффициент γ для нее равен 2,5?

Воспользуемся уравнением Вант-Гоффа.

T₂ >T₁

Теперь обратимся к уравнению Аррениуса, которое устанавливает более строгую связь между константой скорости реакции и температурой.

В июле 1889 г. в немецком журнале «Zeitschrift fur physikalische Chemie» была опубликована основополагающая статья шведского физико-химика Сванте Августа Аррениуса (1859 – 1927 гг.) В статье обсуждались экспериментальные данные химических реакций от 8 различных исследователей. Исследования были опубликованы в открытой печати. Исследователи изучали зависимости скорости выбранных реакций от температуры, и каждый предлагал эмпирическое уравнение, устанавливающее эту связь. Все восемь экспериментаторов изучали разные реакции, а именно:

1) Окисление железа под действием хлората ClO₃ ^- (H₂SO₄)

2) Щелочной гидролиз (омыление)

3. Инверсия тростникового сахара

4. Инверсия тростникового сахара

5. Разложение хлоруксусной кислоты в водном растворе

6. Дегидробромирование дибромянтарной кислоты

Аррениус, тщательно изучив и обобщив эти результаты, предложил уравнение, устанавливающее количественную зависимость константы скорости реакции от температуры

2.11

где k - константа скорости реакции при некоторой температуре

А и В - эмпирические константы для данной реакции, которые находятся графическим способом

Т - абсолютная температура

Уравнение (2.11) показывает, что логарифм константы скорости реакции линейно зависит от обратной абсолютной температуры реакции. В своей статье Аррениус рассматривал отношения констант скоростей реакции для двух различных температур, т.е.

2.12

Этот подход он распространил на все восемь реакций. В связи с тем, что константы скоростей были определены исследователями для конкретно изучаемых температур, у Аррениуса появилась возможность найти величину А из уравнения (1.11) для каждой из восьми реакций. Получив величину А для каждой из реакций, он начал вычислять величины констант скоростей и для других температур, которые были приведены авторами в экспериментальных данных.

Аррениусу удалось показать, что в большинстве случаев, вычисленные им значения совпадали с экспериментальными данными даже лучше, чем при использовании эмпирических уравнений самих авторов исследований. И лишь только для двух наборов экспериментальных данных применение закона Аррениуса оказалось малоэффективным. Причиной этому может быть следующее: возможно, что точность температурных измерений в этих экспериментах была недостаточно высокой. В этой же статье Аррениус рассмотрел вопрос о возможной причине столь сильного влияния температуры на величину константы скорости реакции. Молекулярно-кинетическая теория строения вещества еще не была достаточно разработана, и Аррениус не мог связать рост значений k с увеличением числа реакционных столкновений, т.е. тех столкновений частиц, атомов и молекул, которые приводят к химической реакции. В качестве достаточно убедительной причины температурной чувствительности k не подходило и возможное уменьшение внутреннего трения с увеличением температуры. Поэтому Сванте Аррениус сделал вывод о существовании гипотетического компонента реакции, концентрация которого резко возрастает с увеличением температуры.

Обратимся к уравнению (2.11)

Как было сказано, А и В – эмпирические константы для данной реакции, которые находятся графическим способом. Графики строят по экспериментально полученным значениям констант скорости изучаемой реакции, которые соответствуют конкретно измеренным температурам.

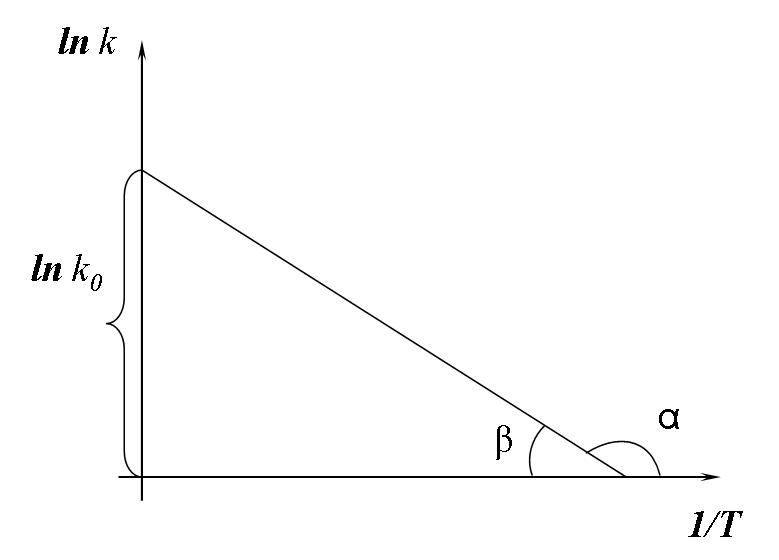
Рисунок 2.2 - Зависимость константы скорости реакции от обратной температуры

Константа А вычисляется как tg угла наклона прямой к оси абсцисс, постоянная В численно равна отрезку, отсекаемому прямой на оси ординат при (при ).

Опытным путем было установлено, что уравнение Аррениуса достаточно точно описывает температурную зависимость константы скорости реакции в широком интервале температур и для реакций различных порядков. Константам А и В уравнения Аррениуса можно приписать некоторое теоретическое значение. В дaльнейшем, при исследовании причин зависимости константы скорости реакции от температуры было введено понятие энергии активации.

Энергия активации - есть минимальная избыточная энергия по сравнению со средним уровнем, которой должны обладать молекулы для протекания химической реакции. Она измеряется в Дж/моль или кДж/моль. Обычно, для химических реакций порядок величины Е_А составляет десятки или сотни кДж/моль.

В - частотный фактор или предэкспоненциальный фактор, имеет ту же размерность, что и константа скорости.

Аррениус установил, что эмпирическая константа А (2.11) связана с другой константой следующим соотношением

2.13

R - универсальная газовая постоянная ( R=8/31Дж/моль к)

Подставив в уравнение (2.11) выражение для А из (2.13) можно получить

2.14

Продифференцировав это уравнение по температуре при Е = const, можно прийти к выражению

2.15

Это уравнение Аррениуса в дифференциальном виде. Из уравнения (2.15) путем интегрирования можно снова получить уравнение (2.14), где В – постоянная интегрирования.

Обозначив В= ln k_{0 ,} из уравнения (2.14), получим

2.16

2.17

Это уравнение Аррениуса в интегральном виде, где k₀ - предэкспоненциальный множитель. Величины E_A и k₀ определяются природой реакции и практически не зависят от температуры.

Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способом. Графический способ заключается в нахождении величины A= - tg(a) по графику зависимости для данной реакции с последующим расчетом E_A по уравнению (2.13), т.е. .

Аналитический способ предполагает применение уравнения (2.16)

для двух различных температур: T₂ > T₁ ; k(T₂)=k₂; k(T₁)=k₁ тогда

В результате вычитания второго уравнения из первого получим выражение

2.18

По уравнению (2.18) можно рассчитать энергию активации данной реакции, используя два экспериментальных значения констант скоростей при двух различных температурах. Или можно провести перерасчет константы скорости с одной температуры на другую при известном значении энергии активации.

Значение и роль предэкспоненциального множителя в уравнении Аррениуса

Рассмотрим некоторые аспекты динамики молекулярных столкновений.

Реакция А + В = С + D идет в прямом направлении. Константа реакции будет выглядеть следующим образом:

2.19

Предэкспоненту k₀ в уравнении Аррениуса попытаемся связать с числом столкновений реагирующих частиц типов А и В в уравнении реакции. Обозначим число столкновений частиц А и В как Z_AB. Предполагается, что А и В частицы идеального газа и рассматривается модель твердых шаров. Тогда можно заключить, что величина k₀ будет являться отношением числа столкновений частиц А и В к произведению их количества

2.20

где Z_AB - число столкновений; n_A и n_B - количество частиц А и В.

В соответствии с кинетической теорией разряженных газов для молекул с короткодействующим потенциалом взаимодействия величина Z_AB равна:

2.21

- сечение реакции

Сечение реакции является внутренней характеристикой процесса перехода отдельной молекулы, атома и т.д. из i-го (начального) в f-е (конечное) квантовое состояние.

- средняя относительная скорость

n_A, n_B - количество частиц А и В.

Для бинарной смеси твердых шаров, имеющих радиусы r_A и r_B, сечение реакции равно:

2.22

2.23

Средняя относительная скорость и приведенная масса определяются обычным образом:

2.24

где k – постоянная Больцмана

2.25

В рамках теории столкновений закон Аррениуса можно представить следующим образом:

2.26

При этом фактор частоты столкновений частиц имеет только слабую функциональную зависимость от температуры.

Для более точной оценки эффективности химических столкновений в уравнение 1.25 вводится понятие стерический фактор Р. Стерический фактор учитывает взаимную ориентацию партнеров бинарных столкновений.