3.Парабола әдісі. (Симпсон формуласы).

(1.7) интегралын жуықтап есептеу үшін функциясын нүктелері арқылы тұрғызылған Лагранж көп мүшесімен алмастырамыз. Яғни

. (1.24)

Осыдан

Сонымен мына формуланы –

(1.25)

Симпсон немесе парабола формуласы деп атайды.

Бұл формуланың парабола формуласы деп атайтын себебі

сызықтарымен шектелген қисық сызықты трапецияның ауданы нүктелері арқылы өтетін парабола және түзулерімен шектелген трапецияның ауданымен алмастырылады (4-сурет).

Симпсон формуласы кесіндісінде былайша жазылады

Бөлшекті индекстерден құтылу үшін

десек,онда Симпсон формуласын былайша жазамыз:

. (1.26)

4-сурет

О х у x_i-1 x_i-1/2 x_i y=f(x) y=L₂(x) + -

Симпсон формуласының жіберетін қатесін қарастырардың алдында, оның үш дәрежелі көпмүше үшін дәл екенін көрсетейік. Шынында да

болса, онда

Осыдан

Екіншіден

екенін ескерсек

формуласын аламыз.

Сонымен Симпсон формуласының үшінші дәрежеге дейінгі кез келген көпмүшелер үшін дәл екенін көрдік.

Енді Симпсон формуласының қатесін қарастыру үшін мына шарттарды қанағаттандыратын

интерполяциялық Эрмит көпмүшелігін пайдаланамыз .

Симпсон формуласы кез келген үш дәрежелі көпмүшеліктер үшін дәл болғандықтан

(1.28)

Енді

десек,онда

мұндағы (1.29)

-Эрмит көпмүшесінің жіберетін қатесі.

кесіндісінде көпмүшесі өзінің таңбасын өзгертпейтін болғандықтан

Сондықтан Симпсон формуласының жіберетін қатесi

. (1.30)

Hемесе

(1.31)

Симпсон формуласының кесіндісінде жіберетін қатесі

Болғандықтан (1.32)

Яғни Симпсон әдісінің кесіндісіндегі дәлдігі .

Лекция 18-21. Жәй дифференциалдық теңдеулерге қойылған Коши есебін шешу

1. Эйлер әдісі

Айталық, функциясы облысында үзіліссіз және Липшитц шарттарын қанағаттандырсын, яғни

(1.1)

теңсіздігі орындалсын, онда жоғарыдан шектелген, яғни , және

(1.2)

(1.3)

есебінің бір ғана шешуі бар.

Енді осы шешуді табу үшін (7)- ші интегралға тік төртбұрыш әдісін қолдану арқылы (6) теңдіктен, торында мына теңдікті аламыз:

(1.4)

Осыдан кезде 0(һ) нөлге ұмтылыды деп шешсек, онда

деп белгілеу арқылы

, (1.5)

теңдіктерін аламыз.

5. теңдігін, әдетте, Эйлер әдісі деп атайды.

Енді кезде осы әдіс бойынша табылған тізбегі (1.2)-(1.3) есебінің шешуіне жинақталатынын, яғни

болатынын қарастырайық.

Ол үшін функциясын нүктесінің кіші аймағында Тэйлор қатарына жіктейміз:

Содан кейін осы теңдікті пайдаланып мәнін есептейміз:

(1.6)

Мұнда (1.2) теңдеуіне сәйкес болатыны есекерілген. Енді (1.6) өрнегінен (1.5) өрнегін шегерсек, онда

Осыдан белгілеуін еңгізіп, әдіс қаталігінің абсолют мәнін бағаласақ:

Соңғы теңсіздікке - Липшитц шартын пайдаланып:

(1.7)

теңсіздігін аламыз, мұндағы

Енді (1.7) теңсіздігін k-ның k=0, 1, ... мәндері үшін ашып жазсақ:

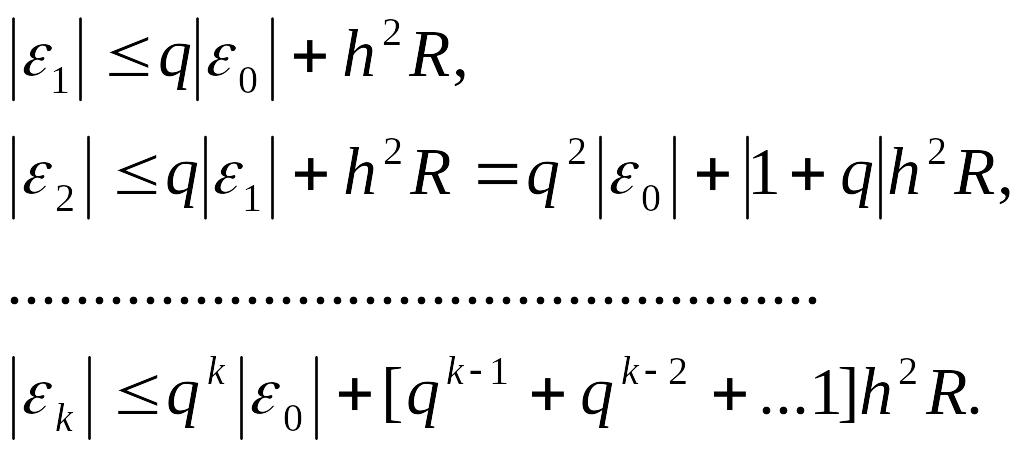
Эйлер әдісі үшін болғандықтан

Ал кезде болатындықтан

Демек, Эйлер әдісі кезінде (1.2) - (1.3) есебінің дәл шешуіне жинақталады және оның жинақталу реті 1-ге тең.